A charged capacitor C1 is discharged through a resistance R by putting switch S in position 1 of circuit shown in figure. When discharge current reduces to I0, the switch is suddenly shifted to position 2. Calculate the amount of heat liberated in resistance R starting from this instant.
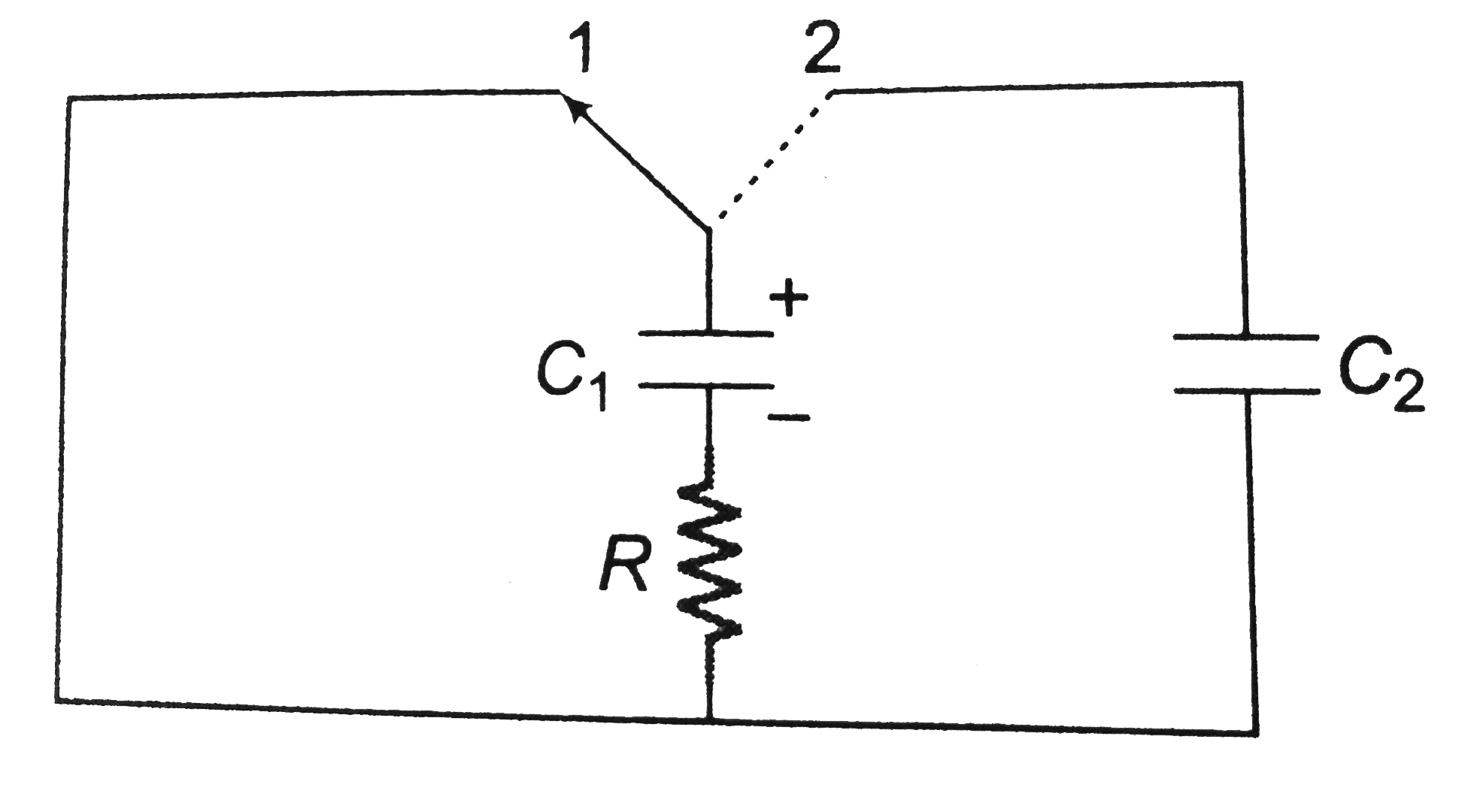
Let the charge on capacitor C1beq0 when the switch was
shifted from position 1 to position 2. just before shifting of
switch, the circuit was as shown in fig 5.202
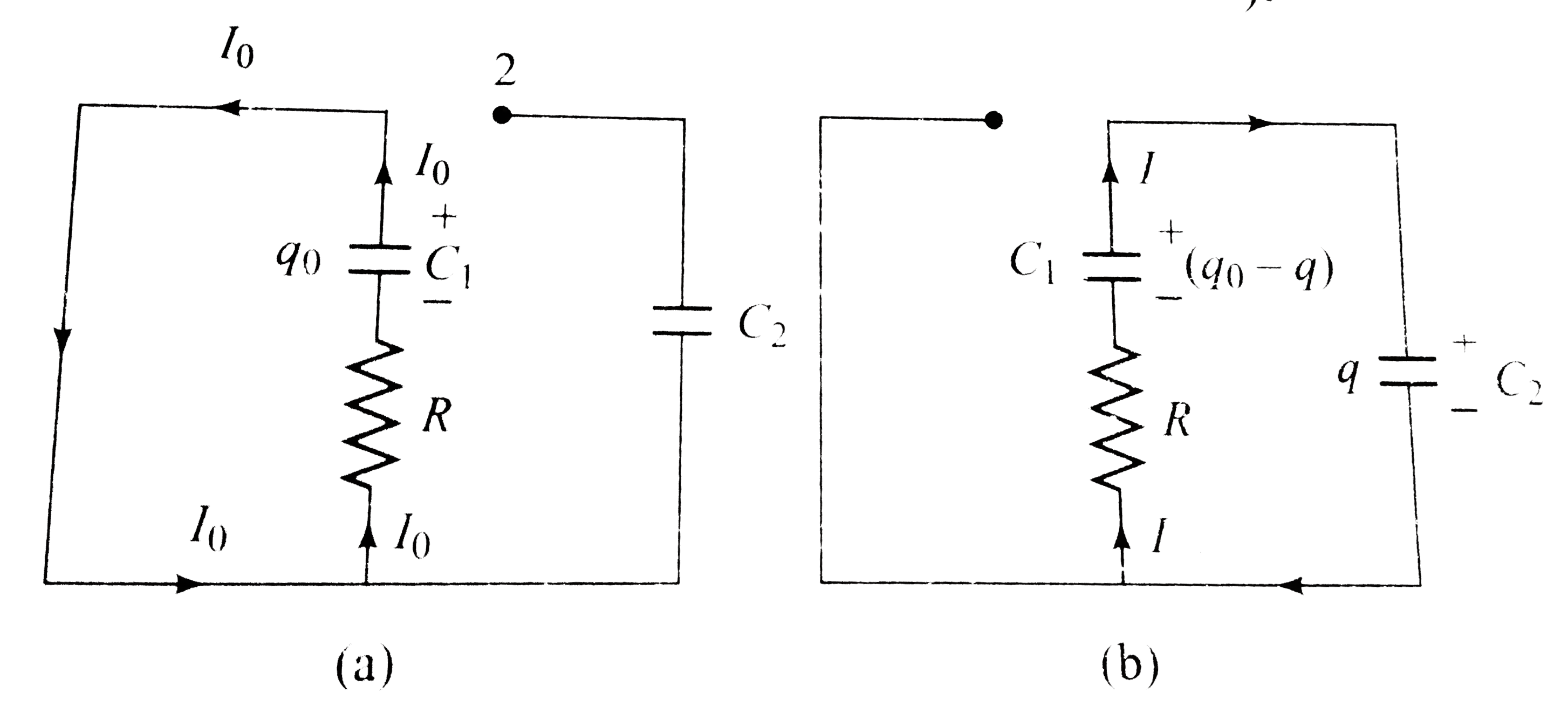
q0C1−I0R=0orq0=I0RC1
When the switch is shifted from position 1 to 2,
the capacitor C1 continues to be discharged while C2 starts
charging. Let at time t, after shiffting of switch to position 2,
charge on capacitor C2 be q and let current through the circuit
be I.
Therefore, charge remaining on C1 is equal to (q0−q) as
shown in fig 5.202 (b). Applying Kirchhoff's voltage law on
the circuit shown in fig. 5.202 (b) we get
qC2+IR−(q0−q)C1=0
or IR=q0−qC1−qC2=(q0C2−qC2)−qC1C1C2
But current , I=dqdt (rate of increase of chargen C2
or R=dpdt=q0C2−q(C1+C2)C1C2
or dpq0C2−q(C1+C2)=dtRC1×C2
But at t = 0, q= 0,
∫q0dqq0C2−q(C1+C2)=∫10dtRC1C2
From the above equation, we get
q=(q0C2C1+C2)[1−e−(C1+C2RC1C2)t]
Substituting q0=I0RC1, we get
q=I0RC1C2C1+C2[1−e−(C1+C2RC1C2)t]
But current
I=dqdt=I0e−C1+C2RC1C2t
in a steady state, the common potential difference across
capacitors is given by
V=q0+0C1+C2=I0RC1C1+C2(using V=C1V1+C2V2C1+C2)
Initially energy stored in C1 was
U1=q202C1=12I20R2C1
In steady state, energy stored in two capacitors is
U2=12C1V2+12C2V2=12(C1+C2)I20R2C21(C1+C2)2=I20R2C212(C1+C2)
Heat generated across resistor R is equal to the loss of
energy stored ni capacitors during redistribution of charge, i.e.,
U1=U2=I20R2C1C22(C1+C2)
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.1
28 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.2
50 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
Similar Questions
A charged capacitor C1 is discharged through a resistance R by putting switch S in position 1 of the circuit as shown in fig.5.201. When the discharge current reduces to i0, the switch is suddenly shifted to position 2. Calculate the amount of heat liberated in resistor R starting form this instant. Also calculate current I through the circuit as a function of time.

View SolutionWhen a capacitor discharges through a resistance R, the time constant is τ and the maximum current in the circuit is i0. Then,
View SolutionThe capacitor C shown in the figure is in steady state condition when switch is shifted from position 1 to position 2.The heat liberated in the process is
_PHY_E05_272_Q01.png)
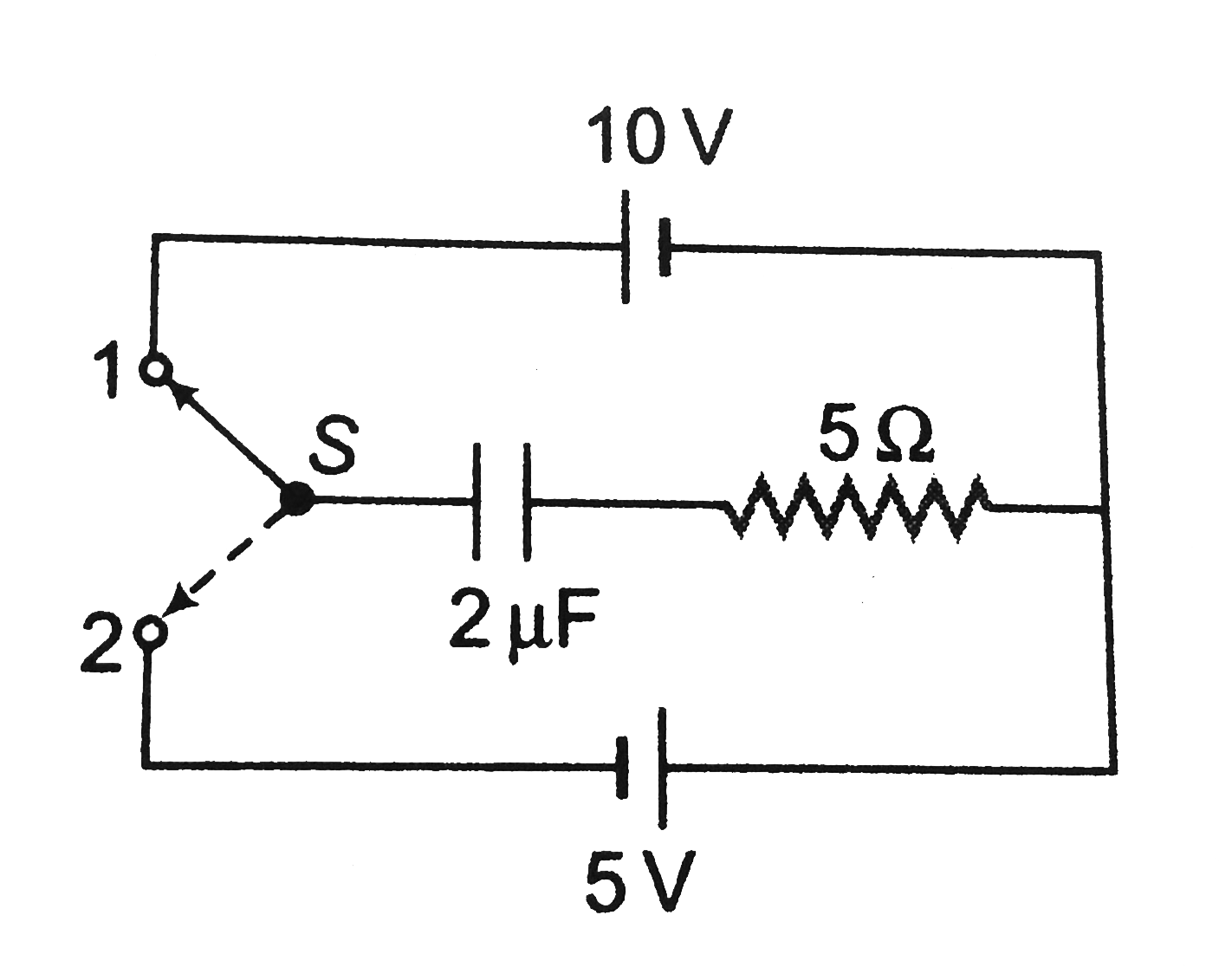
View SolutionIn the circuit shown in figure switch S is thrown to position 1 at t=0. when the current in the resistort is 1A, it is shifted to position 2. the total heat generated in the circuit after shifting to position 2 is
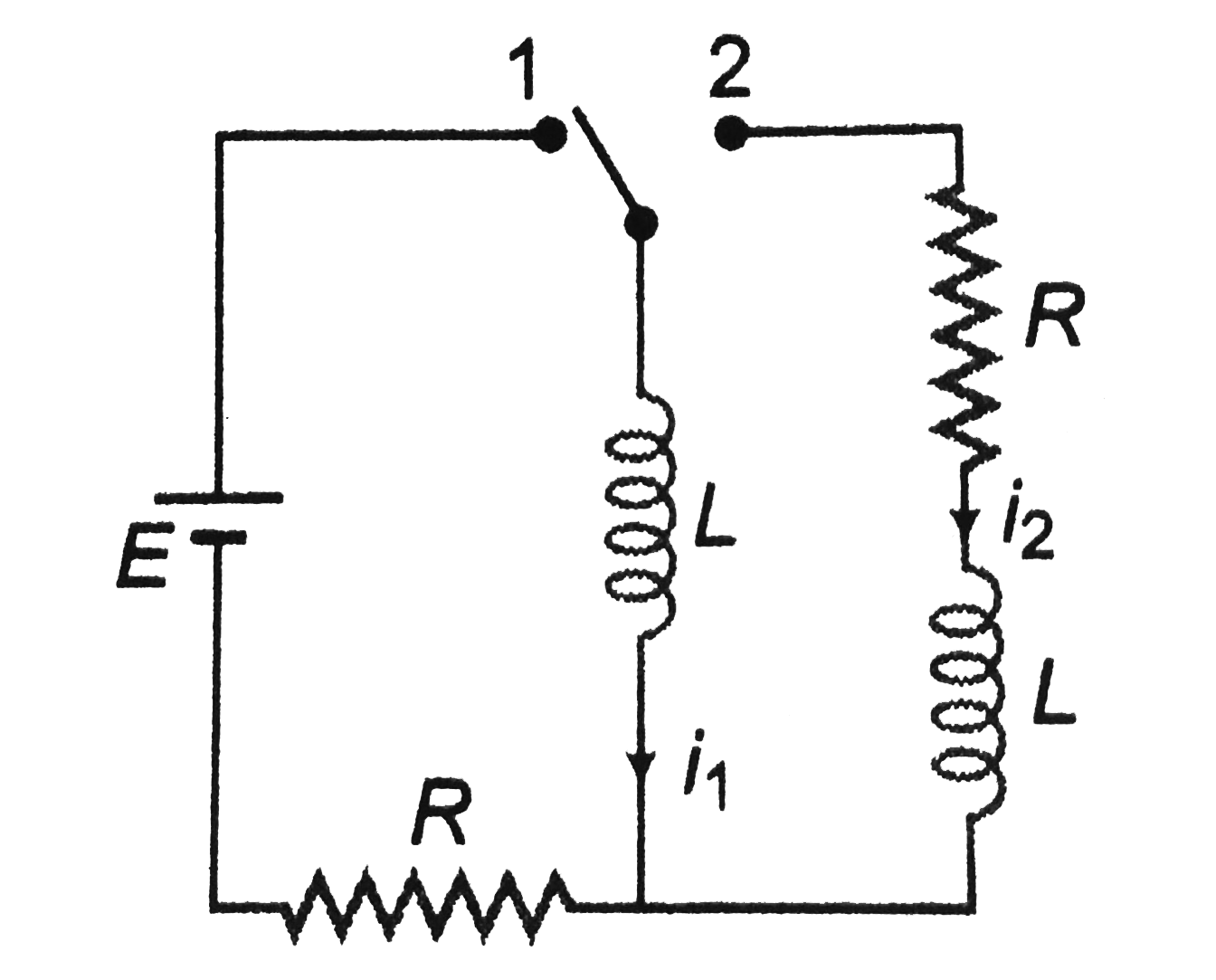
View SolutionIn the circuit shown in the figure The steady state currents i1andi2 in the coils after the switch S is closed are

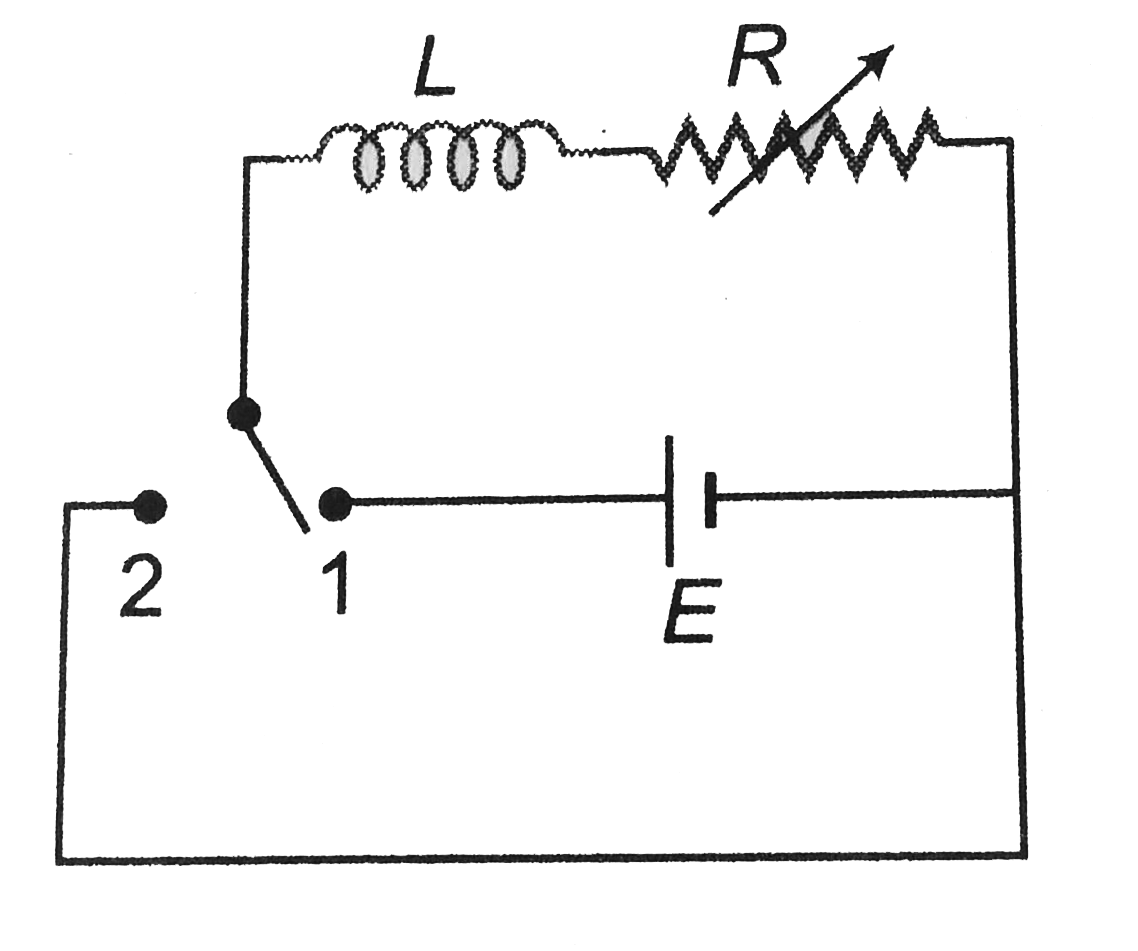
View SolutionIn the circuit shown in the figure initialy the switch in position 1 for a long time, then suddenly at t=0 the switch is shifted to position 2. It is required that a constant current should flow in the circuit, the value of resistance R in the circuit
View SolutionIn the circuit shown switch S is connected to position 2 for a long time and then joined to position 1.The total heat produced in resistance R2 is:

View SolutionInitially, switch S is connected to position 1 for a long time . The net amount of heat generated in the circuit after it is shifted to position 2 is .
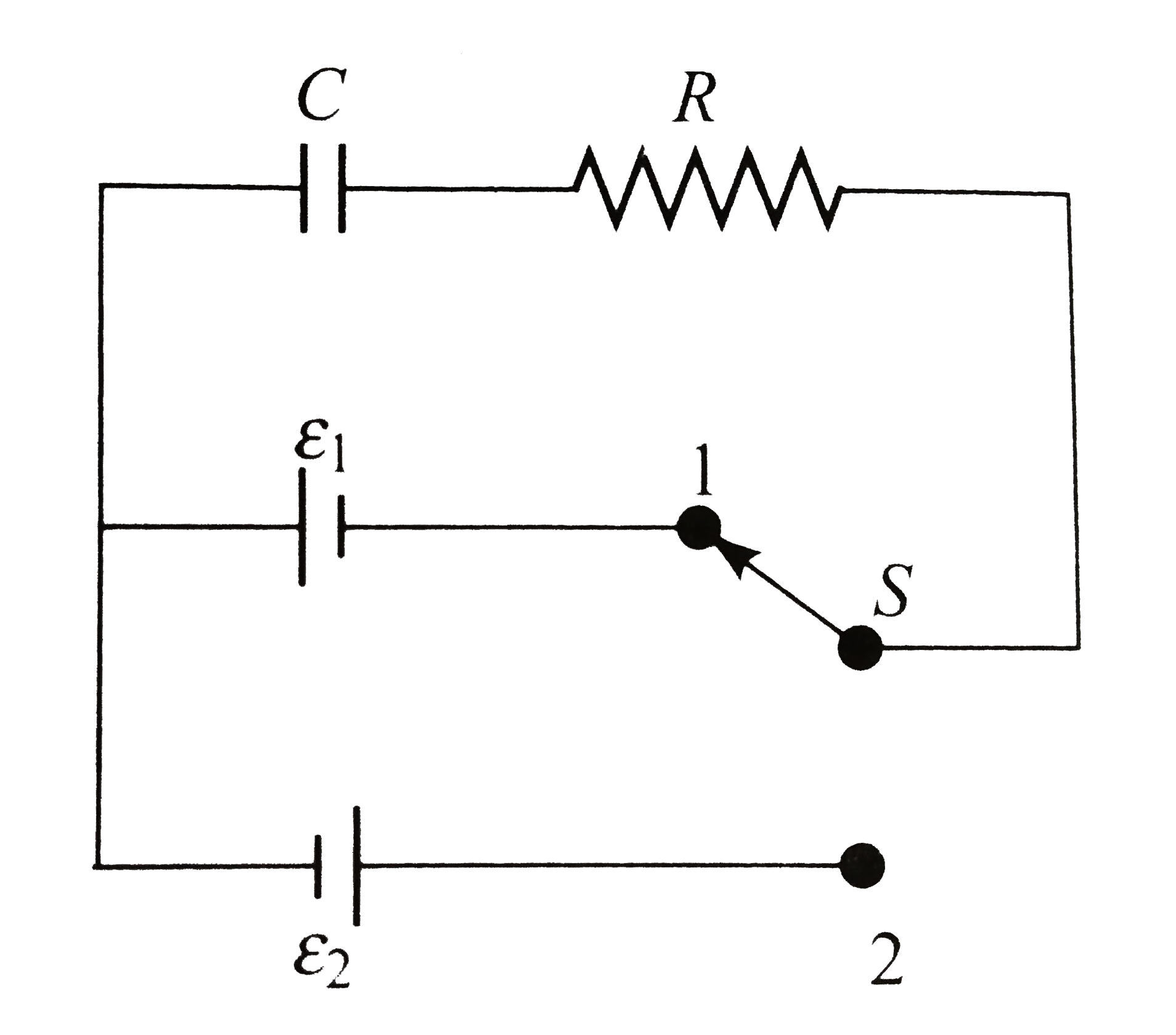
View SolutionIn figure, the switch is in the position 1 for long time, then the switch is shifted to position 2 at t=0. At this instant the value of i1 and i2 are
View SolutionIn the circuit shown below, the switch is in position 1 for a long time. At some moment after that the switch is thrown in position 2. The quantity of heat generated in the resistance of 375 ohm after the switch is changes to position 2 is :
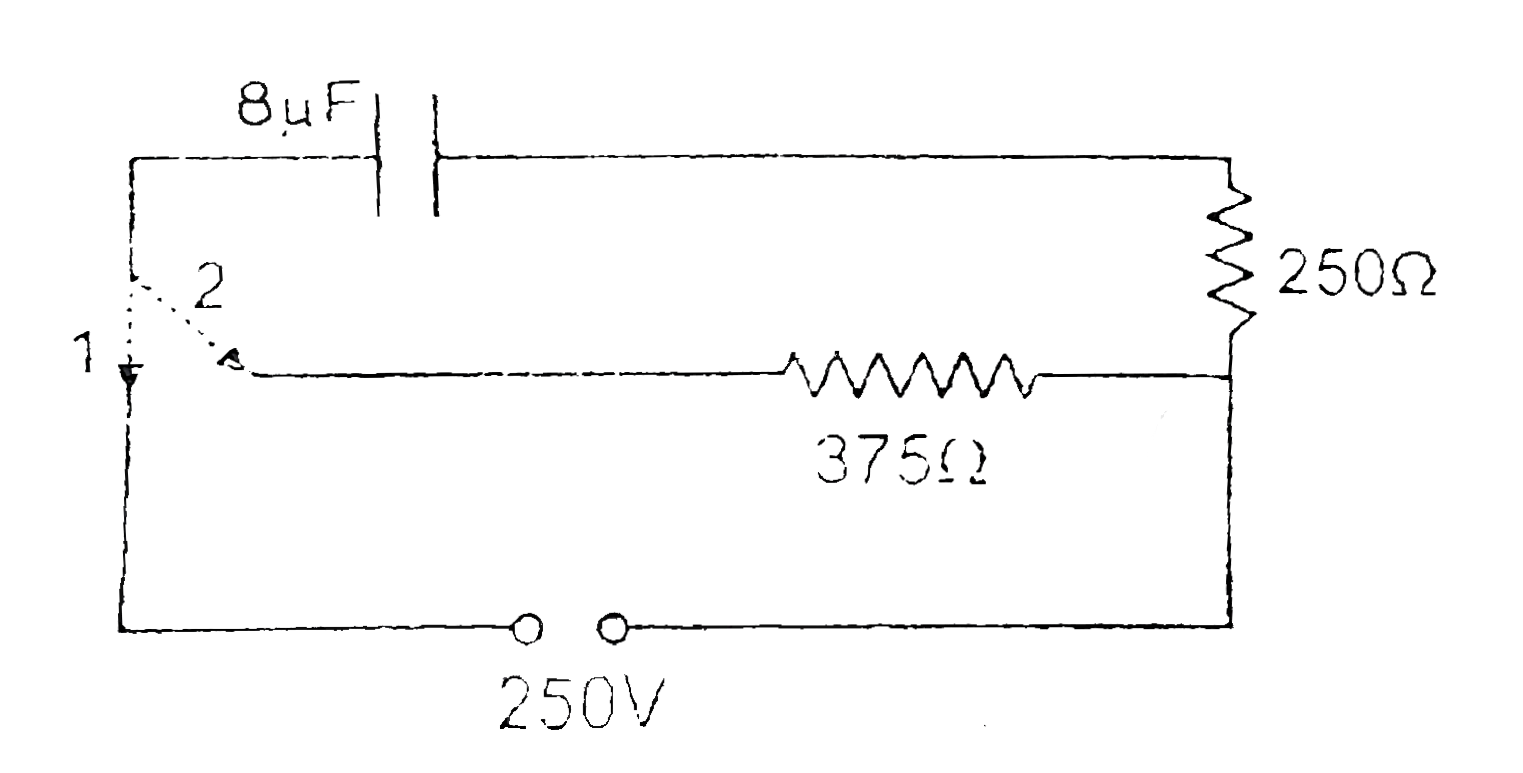
View Solution