If a wire of resistance 20Ω is covered with ice and a voltage of 210V is applied across the wire , then the rate of melting of ice is
8.85gs−1
1.92gs−1
6.56gs−1
none of these
The correct Answer is:C
To solve the problem of determining the rate of melting of ice when a wire of resistance 20Ω is covered with ice and a voltage of 210V is applied across the wire, we can follow these steps:
Step 1: Calculate the Current (I) through the Wire
Using Ohm's Law, we can find the current flowing through the wire:
I=VR
Where:
- V=210V (voltage applied)
- R=20Ω (resistance of the wire)
Substituting the values:
I=210V20Ω=10.5A
Step 2: Calculate the Power (P) Dissipated in the Wire
The power dissipated in the wire can be calculated using the formula:
P=I2R
Substituting the values:
P=(10.5A)2×20Ω=110.25×20=2205W
Step 3: Determine the Rate of Heat Generation
The rate of heat generation (which is equal to the power calculated) is:
Rate of heat generation=P=2205J/s
Step 4: Calculate the Rate of Melting of Ice
The rate of melting of ice can be calculated using the latent heat of fusion of ice. The latent heat L of ice is approximately 336J/g. The mass of ice melted per second can be calculated using the formula:
mt=PL
Where:
- P=2205J/s (power)
- L=336J/g (latent heat of fusion)
Substituting the values:
mt=2205J/s336J/g≈6.5625g/s
Final Answer
The rate of melting of ice is approximately 6.56g/s.
---
Using Ohm's Law, we can find the current flowing through the wire:
I=VR
Where:
- V=210V (voltage applied)
- R=20Ω (resistance of the wire)
I=210V20Ω=10.5A
The power dissipated in the wire can be calculated using the formula:
P=I2R
Substituting the values:
P=(10.5A)2×20Ω=110.25×20=2205W
The rate of heat generation (which is equal to the power calculated) is:
Rate of heat generation=P=2205J/s
The rate of melting of ice can be calculated using the latent heat of fusion of ice. The latent heat L of ice is approximately 336J/g. The mass of ice melted per second can be calculated using the formula:
mt=PL
Where:
- P=2205J/s (power)
- L=336J/g (latent heat of fusion)
mt=2205J/s336J/g≈6.5625g/s
The rate of melting of ice is approximately 6.56g/s.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Multiple Correct5videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Assertion - Reasoning6videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Subjective8videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer Type4videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based8videos
INDUCTANCE
Similar Questions
A coil of water of resistance 50Ω is embedded in a block of ice and a potential difference of 210 V is applied across it. The amount of ice which melts in 1 second is [ latent heat of fusion of ice =80calg−1]
View SolutionABCD is a square where each side is a uniform wire of resistance 1Ω. A point E lies on CD such that if a uniform wire of resistance 1Ω is connected across AE and constant potential difference is applied across A and C, then B and E are equipotential.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A uniform wire of resistance 36Ω is bent in the form of a circle. The effective resistance across the points A and B is
 A5ΩB15ΩC7.2ΩD30Ω
A5ΩB15ΩC7.2ΩD30Ω
A uniform wire of resistance 4Ω is bent into circle of radius r. As specimen of the same wire is connected along the dimeter of the circle. What is the equivalent resistance across the ends of this wire?
View SolutionA wire of resistance 4Ω is stretched to twice its original length. The resistance of stretched wire would be
View SolutionA wire of resistance(10Ω) is stretched to twice its original length. The resistance of half of the streached wire is
View SolutionFor a cell of e.m.f. 2 V , a balance is obtained for 50 cm of the potentiometer wire. If the cell is shunted by a 2Ω resistor and the balance is obtained across 40 cm of the wire, then the internal resistance of the cell is
View SolutionA current 0.2A flows in a wire of resistance 15Ω. Find the potential difference across the ends of the wire.
View SolutionA uniform wire of resistance 18Ω is bent in the form of a circle. The effective resistance across the points a and b is
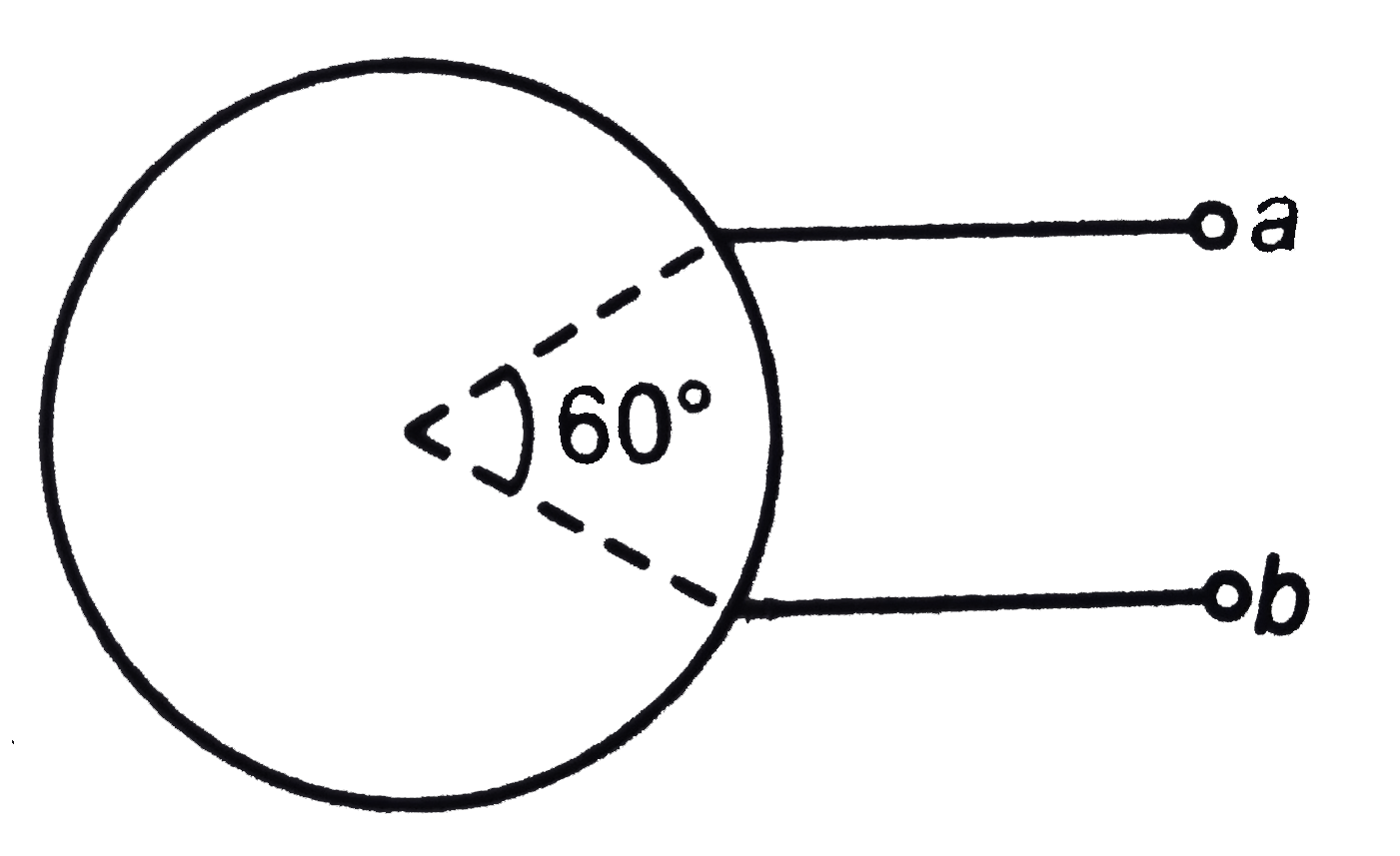 View Solution
View SolutionIn a potentiometer experiment, the galvanometer shows no deflection when a cell is connected across 60cm of the potentiometer wire. If the cell is shunted by a resistance of 6Ω, the balance is obtained across 50cm of the wire. The internal resistance of the cell is
View Solution

