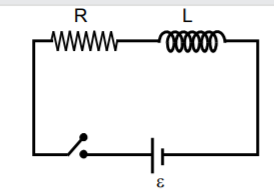
The switch S in the circuit diagram is closed at t = 0. The charge on capacitors at any time is
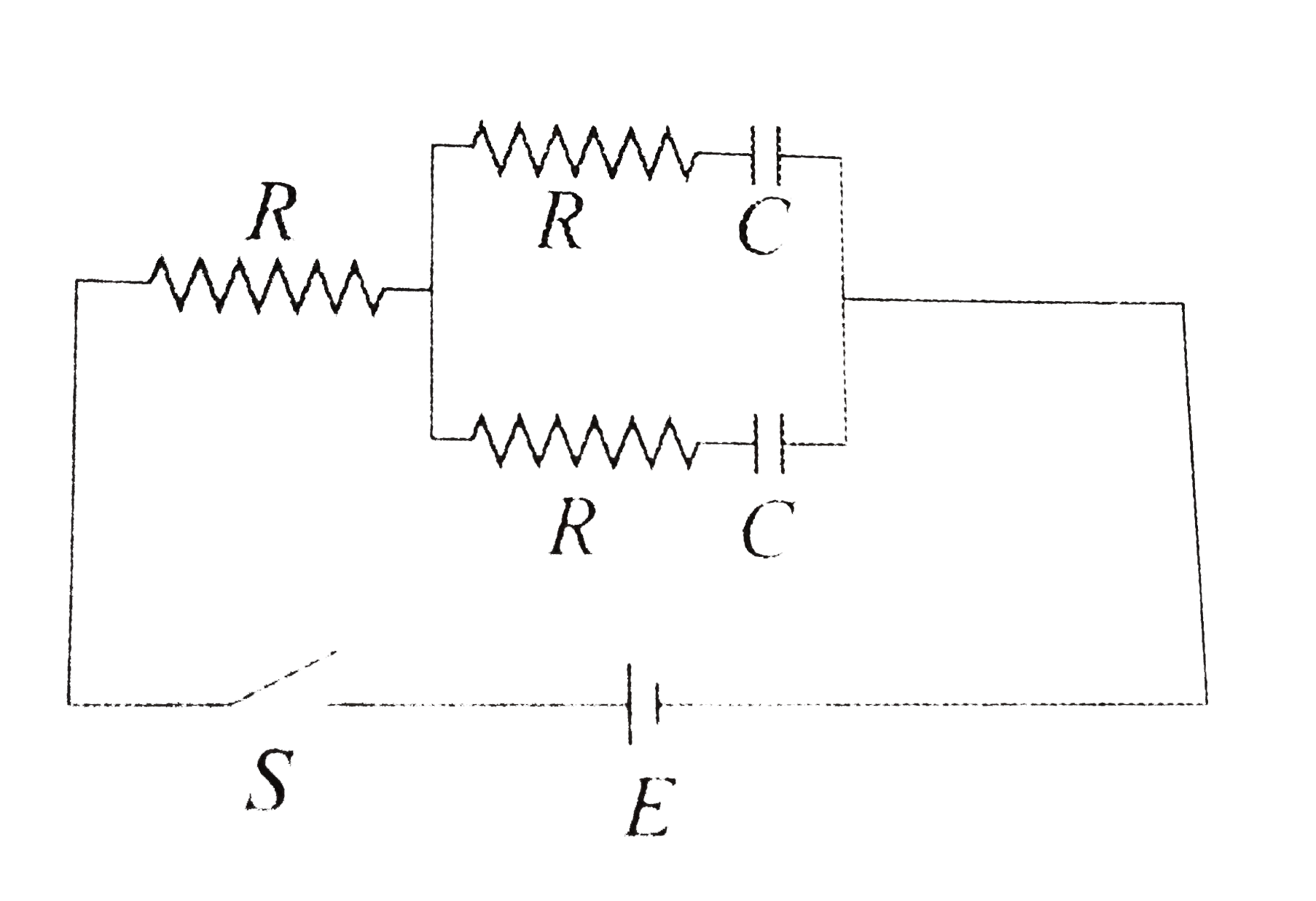
qt=EC(1−e−2t/3RC)
qt=EC(1−e−t/2RC)
qt=EC(1−e−t/3RC)
qt=EC(1−e−3t/2RC)
The correct Answer is:C
c. Applying KVL, we get
12=dqdtorI=2dqdt
E−IR−12R−qC=0
or E−32IR−qC=0
or E−32×2dqdtR−qC=0
qt=EC(1−e−t/3RC).
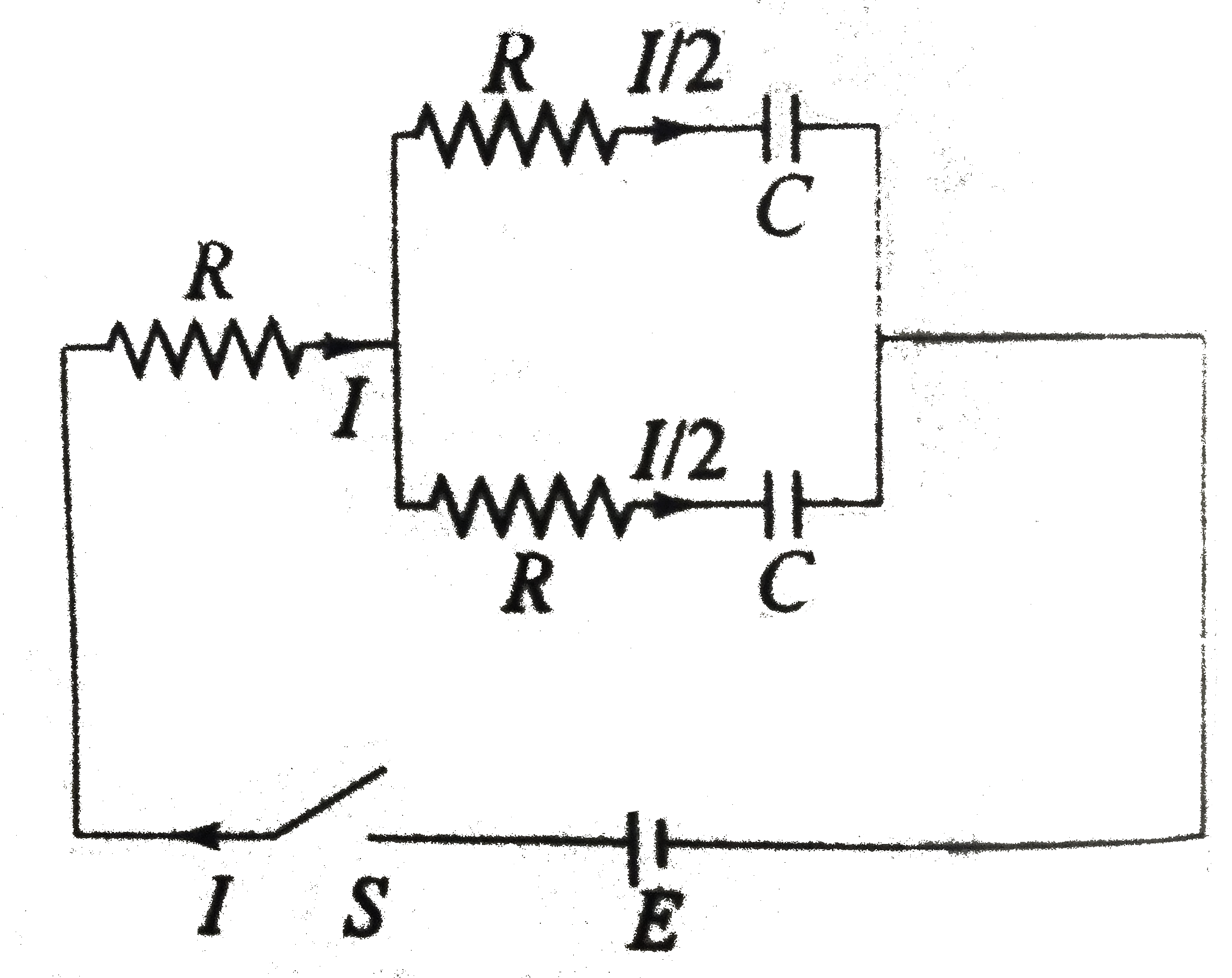
Similar Questions
The switch shown n the figure is closed at t=0. The charge on the capacitor as a function of time is given by
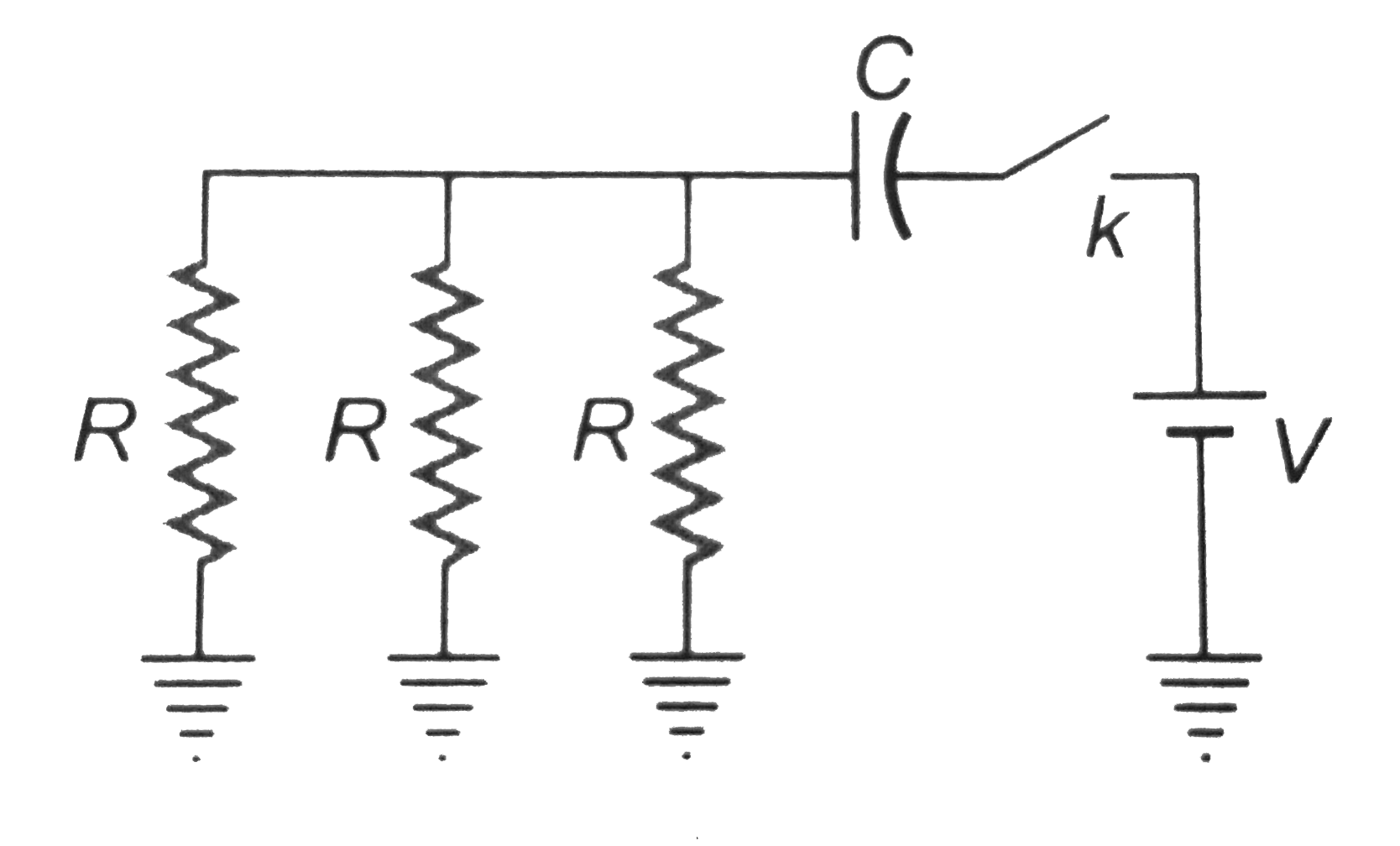
View SolutionIn the given circuit, the switch S is closed at time t = 0 . The charge Q on the capacitor at any instant t is given by Q(t)=Q(1−e−αt). Find the value of Q0 and α in terms of given parameters as shown in the circuit.
 .
.
View SolutionIn the following circuit, the switch S is closed at t = 0. The charge on the capacitor C1 as a function of time will be given by (Ceq=C1C2C1+C2)

View SolutionPassage-III
In the circuit shown, the battery is ideal with emf V. The capacitor is initially uncharged. The switch is closed at time t = 0
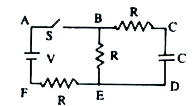
The current in branch containing capacitors at any time t is
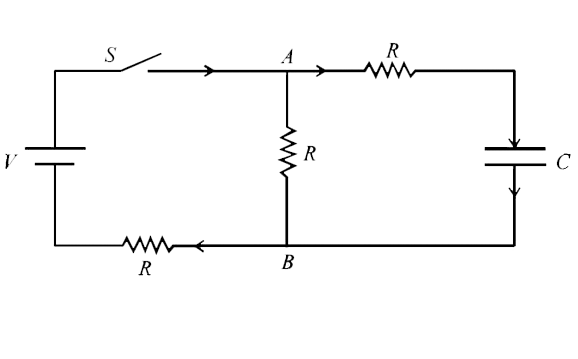
View SolutionIn the circuit shown in Figure, the battery is an ideal one, with emf V. The capacitor is initially uncharged. The switch S is closed at time t = 0 .
(a) Find the charge Q on the capacitor at time t.
(b) Find the current in AB at time t. What is its liniting value as t→∞:
 .
.
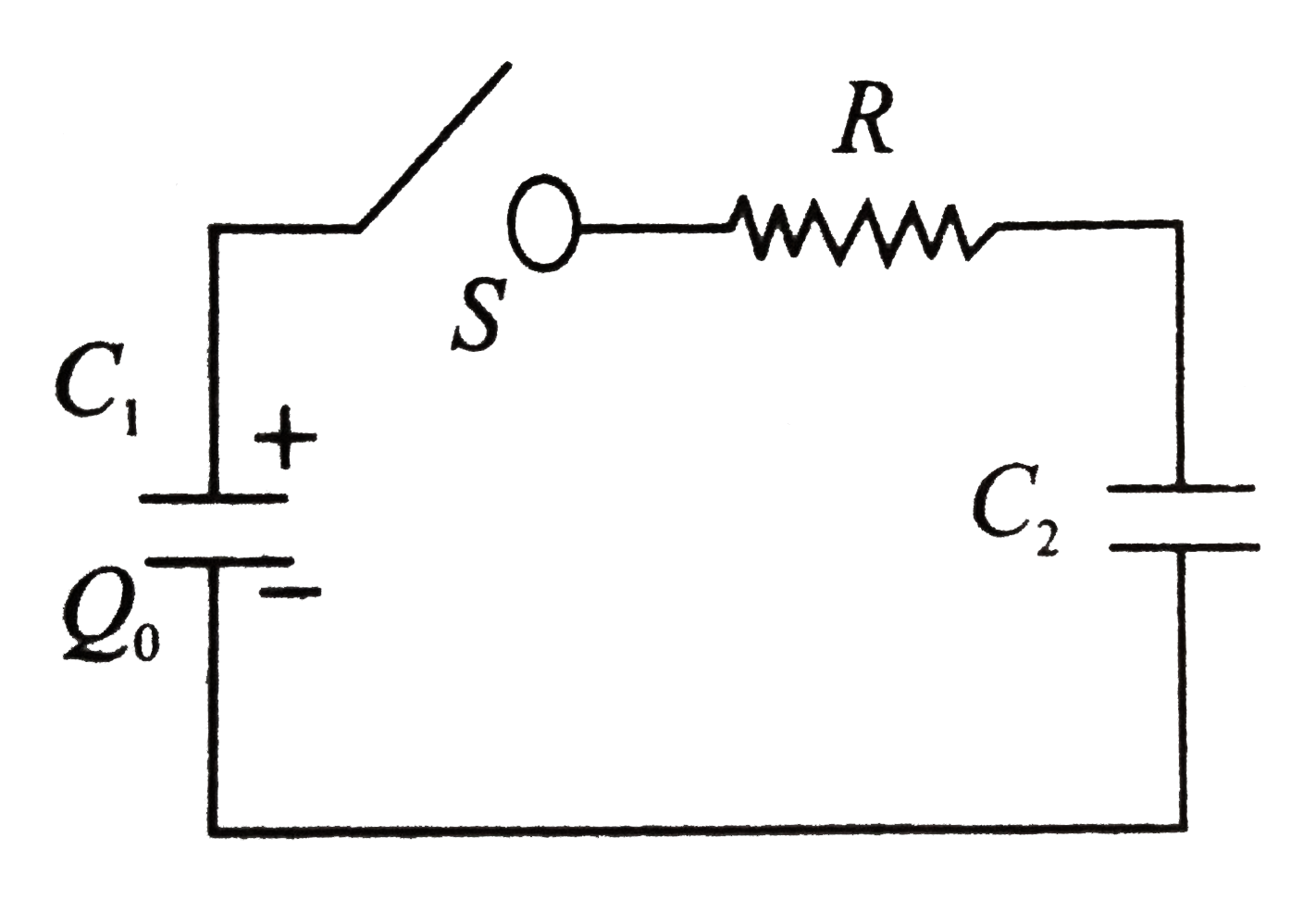
View SolutionIn the circuit shown, the capacitor C1 is initially charged with charge q0. The switch S is closed at time t = 0 . The charge on C2 after time t is
View SolutionThe switch S is closed in the circuit shown at time t=0 . The current in the resistor at t=0 and t=∞ are respectively .
View SolutionIn the given circuit switch is closed at t=0. The charge flown in time t=Tc (where Tc is time constant).
View SolutionIn the circuit shown in fig, if the switch S is closed at t=0 , the capacitor charges with a time constant

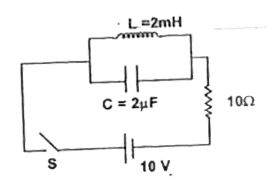
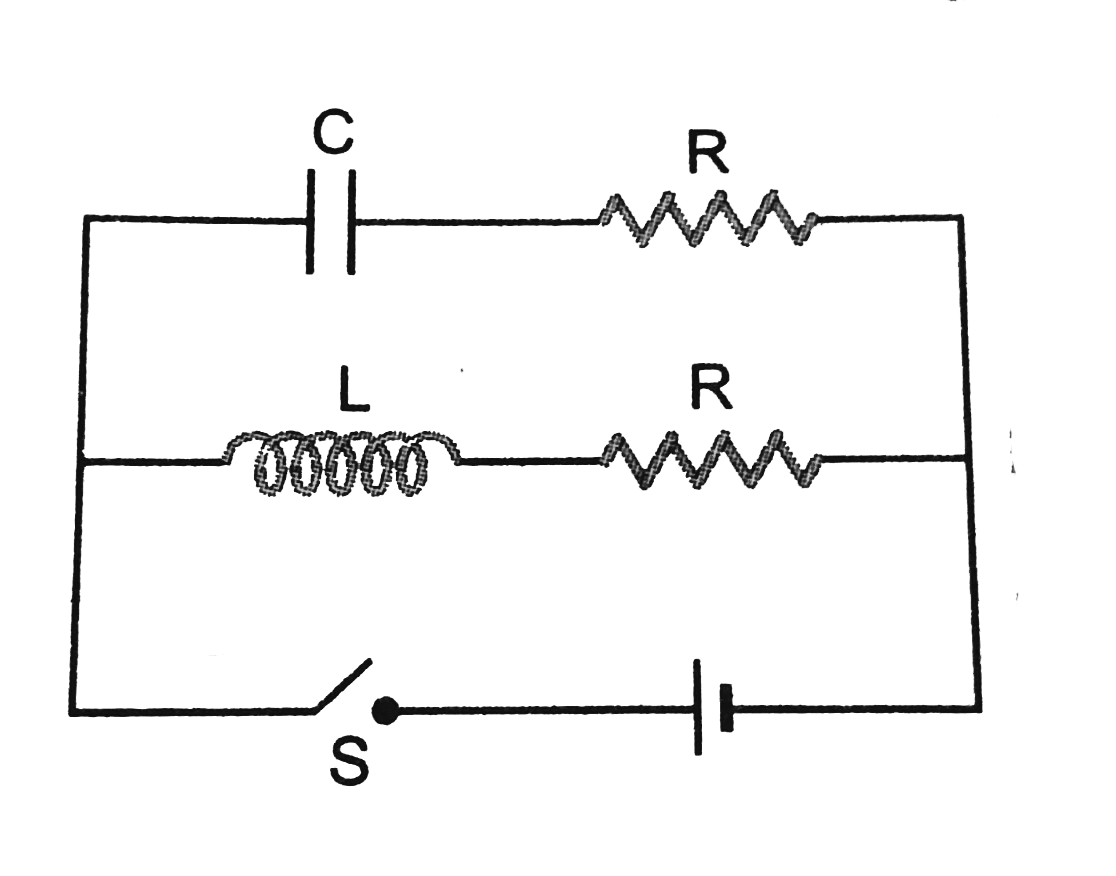
View SolutionIn the circuit shown if Fig. the switch S is closed at time t = 0. The current through the capacitor and inductor will be equal at time t equal (given R=√L/C
View Solution
