A capacitor of capacitance 10mF is charged up a potential difference of 2V and then the cell is removed. Now it is connected to a cell of emf4V and is charged fully. In both cases the polarities of the two cells are in the same directions. Total heat produced in the second charging process is :
10mJ
20μJ
40μJ
80μJ
The correct Answer is:B
To solve the problem step by step, we will follow the process of calculating the energy stored in the capacitor, the charge on the capacitor, and the heat produced during the charging process.
Step 1: Calculate the initial energy stored in the capacitor
The formula for the energy stored in a capacitor is given by:
U=12CV2
Where:
- U is the energy in joules,
- C is the capacitance in farads,
- V is the voltage in volts.
Given:
- C=10mF=10×10−3F
- V=2V
Substituting the values:
U=12×(10×10−3)×(22)=12×10×10−3×4=20×10−3=20mJ
Step 2: Calculate the initial charge on the capacitor
The charge Q on a capacitor is given by:
Q=C×V
Substituting the values:
Qinitial=10×10−3×2=20mC
Step 3: Calculate the final energy stored in the capacitor after connecting to the 4V battery
Using the same energy formula:
Ufinal=12CV2
Where V=4V:
Ufinal=12×(10×10−3)×(42)=12×10×10−3×16=80×10−3=80mJ
Step 4: Calculate the final charge on the capacitor
Using the charge formula again:
Qfinal=C×V
Substituting the values:
Qfinal=10×10−3×4=40mC
Step 5: Calculate the charge flow through the battery
The charge flow ΔQ is given by:
ΔQ=Qfinal−Qinitial=40mC−20mC=20mC
Step 6: Calculate the work done by the battery
The work done W by the battery is given by:
W=ΔQ×V
Where V=4V:
W=20×10−3×4=80mJ
Step 7: Calculate the heat produced in the process
The heat Qh produced can be calculated using:
Qh=W−(Ufinal−Uinitial)
Substituting the values:
Qh=80mJ−(80mJ−20mJ)=80mJ−60mJ=20mJ
Final Answer
The total heat produced in the second charging process is:
20mJ
The formula for the energy stored in a capacitor is given by:
- U is the energy in joules,
- C is the capacitance in farads,
- V is the voltage in volts.
- C=10mF=10×10−3F
- V=2V
The charge Q on a capacitor is given by:
Using the same energy formula:
Using the charge formula again:
The charge flow ΔQ is given by:
The work done W by the battery is given by:
The heat Qh produced can be calculated using:
The total heat produced in the second charging process is:
Similar Questions
A capacitor of capacitnace C is charged to a potential difference V and then disconnected from the battery. Now it is connected to an inductor of inductance L at t=0. Then
 View Solution
View SolutionA capacitor of capacitance C is initially charged to a potential difference of V volt. Now it is connected to a battery of 2V with oppoiste polarity. The ratio of heat generated to the final enegry stored in the capacitor will be
View SolutionA capacitor of capacitance C is charged to a potential difference V from a cell and then disconncted from it. A charge +Q is now given to its positive plate. The potential difference across the capacitor is now
View SolutionA capacitor of capacitance C is charged to a potential difference V from a cell and then disconncted from it. A charge +Q is now given to its positive plate. The potential difference across the capacitor is now
View SolutionA capacitor of capacitance 2μF is charged to a potential difference of 5V. Now, the charging battery is disconected and the capacitor is connected in parallel to a resistor of 5Ω and another unknown resistor of resistance R as shown in figure. If the total heat produced in 5Ω resistance is 10μJ then the unknown resistance R is equal to
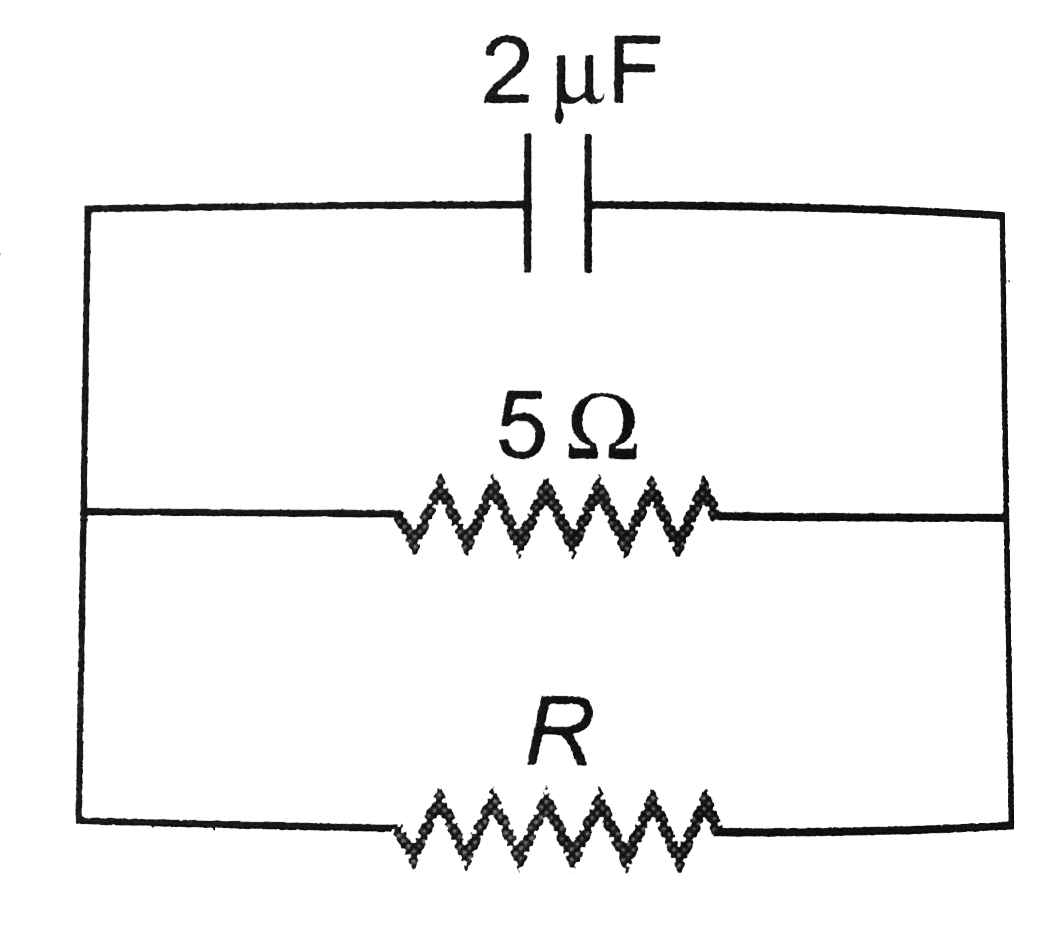 View Solution
View SolutionA capacitor of capacitance 2μF is charged to a potential difference of 5V. Now, the charging battery is disconected and the capacitor is connected in parallel to a resistor of 5Ω and another unknown resistor of resistance R as shown in figure. If the total heat produced in 5Ω resistance is 10μJ then the unknown resistance R is equal to
 View Solution
View SolutionA capacitor of capacitance 5μF is charged to potential 20V and isolated. Now, an uncharged capacitor is connected in parallel to it. If the charge distributes equally on these capacitors, find total energy stored in capacitors.
View SolutionA capacitor of capacitance 10μF is charged to a potential 50V with a battery. The battery is now disconnected and an additional charge 200μC is given to the positive plate of the capacitor. The potential difference across the capacitor will be.
View SolutionA capacitor of capacitance C is charged to a potential difference V0 and then connected with a resistance and a battery of EMF 3V0 such that the positively charged plate of the capacitor is connected to the positive terminal of the battery. The total heat generated in the resistance until the current in the circuit becomes zero is n(CV20). the value of n is ________.
View SolutionA capacitor of capacitance C1 is charged to a potential difference V and then connected with an uncharged capacitor of capacitance C2 a resistance R. The switch is closed at t = 0. Choose the correct option(s):
View Solution

