A moving coil galvanometer of resistance 100Ω is used as an ammeter using a resistance 0.1Ω. The maximum diflection current in the galvanometer is 100μA. Find the minimum current in the circuit so that the ammeter shows maximum deflection
100.1mA
1000.1mA
10.01mA
1.01mA
The correct Answer is:A
To solve the problem, we need to find the minimum current in the circuit (I) that will cause the galvanometer to show maximum deflection. We can use the relationship between the current through the galvanometer (Ig), the total current (I), and the shunt resistance (S).
1. Identify the given values:
- Resistance of the galvanometer (Rg) = 100 Ω
- Shunt resistance (S) = 0.1 Ω
- Maximum deflection current in the galvanometer (Ig) = 100 μA = 100 × 10^(-6) A
2. Use the formula for the current in the circuit:
The relationship between the total current (I), the current through the galvanometer (Ig), and the shunt resistance (S) can be expressed as:
I−IgS=IgRg
This equation states that the potential difference across the shunt resistance (I - Ig) is equal to the potential difference across the galvanometer (Ig).
3. Rearranging the equation:
Rearranging the above equation gives:
I−Ig=IgRg⋅S
Therefore,
I=Ig+Ig⋅SRg
4. Substituting the values:
Now substitute the known values into the equation:
I=100×10−6+100×10−6⋅0.1100
5. Calculating the second term:
I=100×10−6+100×10−6⋅0.1100=100×10−6+0.1×10−6
I=100×10−6+0.1×10−6=100.1×10−6
6. Converting to milliampere:
To convert the current into milliampere:
I=100.1×10−6 A=100.1 mA
Final Answer:
The minimum current in the circuit so that the ammeter shows maximum deflection is 100.1 mA.
- Resistance of the galvanometer (Rg) = 100 Ω
- Shunt resistance (S) = 0.1 Ω
- Maximum deflection current in the galvanometer (Ig) = 100 μA = 100 × 10^(-6) A
The relationship between the total current (I), the current through the galvanometer (Ig), and the shunt resistance (S) can be expressed as:
I−IgS=IgRg
This equation states that the potential difference across the shunt resistance (I - Ig) is equal to the potential difference across the galvanometer (Ig).
Rearranging the above equation gives:
I−Ig=IgRg⋅S
Therefore,
I=Ig+Ig⋅SRg
Now substitute the known values into the equation:
I=100×10−6+100×10−6⋅0.1100
I=100×10−6+100×10−6⋅0.1100=100×10−6+0.1×10−6
I=100×10−6+0.1×10−6=100.1×10−6
To convert the current into milliampere:
I=100.1×10−6 A=100.1 mA
The minimum current in the circuit so that the ammeter shows maximum deflection is 100.1 mA.
Similar Questions
A galvanometer has resistance 1Ω. Maximum deflection current through it is 0.1 A
View SolutionA galvanometer of resistance 50Ω is converted into an ammeter by connecting a low resistance (shunt) of value 1Ω in parallel to the galvanometer, S. If full - scale deflection current of the galvanometer is 10 mA, then the maximum current that can be measured by the ammeter is -
View Solution
Knowledge Check
- Question 1 - Select One
A galvanometer of resistance 70Ω, is converted to an ammeter by a shunt resistance r3=0.03Ω. The value of its resistance will become
A0.025ΩB0.022ΩC0.035ΩD0.030Ω
A galvanometer of resistance 1000Ω gives full-scale deflection for a current of 1mA. To measure a P.D of 10V, the resistance to be connected with the galvanometer is
View SolutionA moving coil galvanometer has resistance 50Ω and it indicates full deflection at 4 m A current. A voltmeter is made using this galvanometer and a 5kΩ resistance. The maximum voltmeter, will be close be :
View SolutionA galvanometer of 50Ω resistance when connected across the terminals of a battery of emf 2V along with the resistance 200Ω the deflection produced in the galvanometer is 10 divisions. If the total number of divisions on the galvanometer ·scale on either side of central zero is 30, then the maximum current that can pass through the galvanometer is
View SolutionA voltmeter which can measure 2 V isconstructed by using a galvanometer of resistance 12Ω and that produces maximum deflection for the current of 2mA. Then the resistance R is
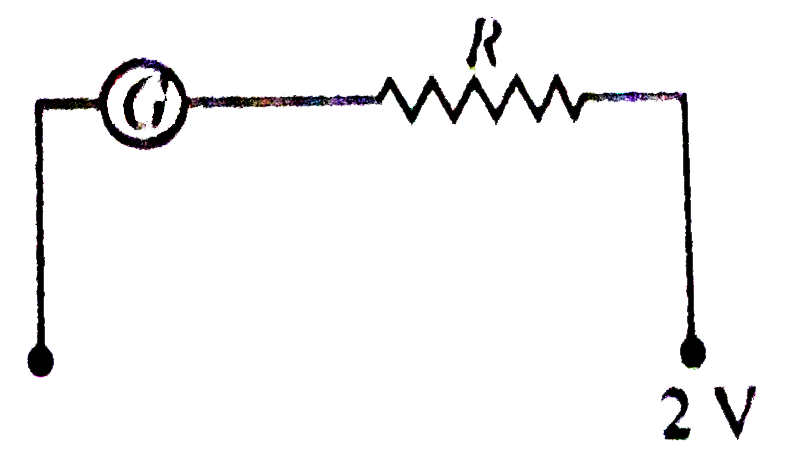 View Solution
View SolutionRange of the ammeter is 5 ampere and full scale diflection current is 0.5mA. If resistance of galvanomenter is 50Ω then find shurt resistance.
 View Solution
View SolutionThe senstivity of a galvanometer that measures current is decreased by 1/40 times by using shunt resistance of 10Ω . Then, the value of the resistance of the galvanometer is
View SolutionA galvanometer of resistance 100Ω gives full scale deflection for 10mA current. What should be the value of shunt, so that it can measure a current of 100mA?
View Solution

