Focal length of a thin lens in air is 10cm. Now, medium on one side of the lens is replaced by a medium of refractive inidex μ=2. The radius of curvature of the surface of lens, in contact with the medium, is 20cm. Find the new focal length.
To find the new focal length of the thin lens after one side is immersed in a medium with a refractive index of μ=2, we can use the lens maker's formula. The formula is given by:
1f=(μ−1)(1R1−1R2)
1. Identify the Given Values:
- Focal length in air, f=10cm
- Refractive index of the medium, μ=2
- Radius of curvature of the surface in contact with the medium, R1=20cm (convex surface)
- Since the lens is thin, we assume the other radius of curvature R2 is infinite (for a thin lens, one side is flat).
2. Determine the Sign Convention:
- For a convex surface, R1 is positive, so R1=+20cm.
- For a flat surface, R2 is considered infinite, so R2=∞ (which means 1R2=0).
3. Apply the Lens Maker's Formula:
- Substitute the values into the lens maker's formula:
1f=(μ−1)(1R1−1R2)
1f=(2−1)(120−0)
1f=1⋅120
1f=120
4. Calculate the New Focal Length:
- Rearranging gives:
f=20cm
5. Final Result:
- The new focal length of the lens when one side is immersed in a medium with a refractive index of 2 is:
f=20cm
Summary:
The new focal length of the lens after one side is immersed in a medium with a refractive index of 2 is 20cm.
- Focal length in air, f=10cm
- Refractive index of the medium, μ=2
- Radius of curvature of the surface in contact with the medium, R1=20cm (convex surface)
- Since the lens is thin, we assume the other radius of curvature R2 is infinite (for a thin lens, one side is flat).
- For a convex surface, R1 is positive, so R1=+20cm.
- For a flat surface, R2 is considered infinite, so R2=∞ (which means 1R2=0).
- Substitute the values into the lens maker's formula:
1f=(μ−1)(1R1−1R2)
1f=(2−1)(120−0)
1f=1⋅120
1f=120
- Rearranging gives:
f=20cm
- The new focal length of the lens when one side is immersed in a medium with a refractive index of 2 is:
f=20cm
The new focal length of the lens after one side is immersed in a medium with a refractive index of 2 is 20cm.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Solved Examples15videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.114videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
Similar Questions
A planocovex lens is made of a material of refractive in μ=1.5 The radius of curvature of curved surface of the lens is 20.cm. If its plane surface3 is silvered, the focal length of the silvered lens will be
View SolutionFocal length of convex lens in air is 16 cm (μglass=1.5). Now the lens is submerged in liquid of refractive index 1.42. Find the ratio of focal length in medium to focal length in air has closest value
View SolutionFocal length of a convex lense in air is 20cm. and of concave lens 40cm. Find the position of final image.
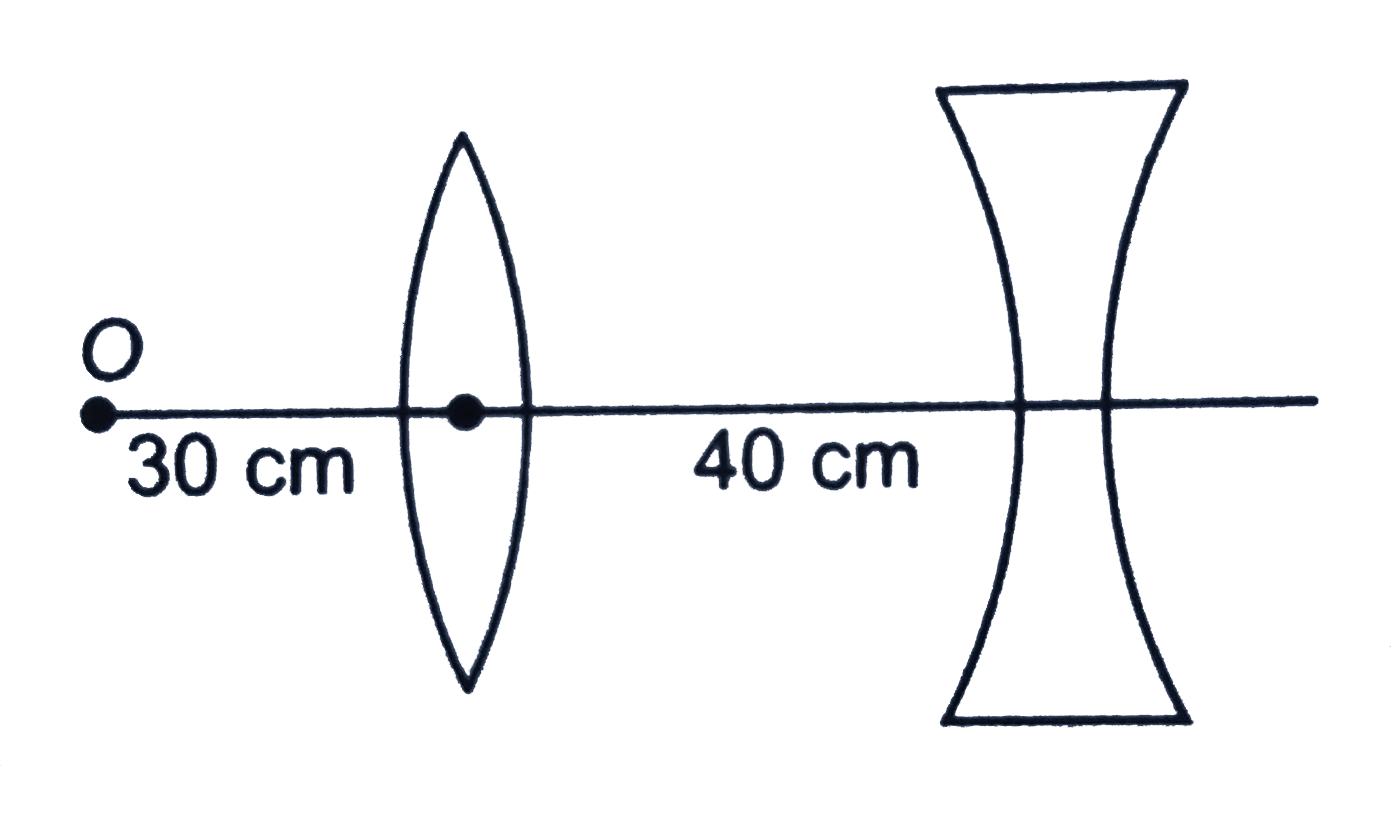 View Solution
View SolutionFocal length of convex lens in air is 16 cm (μglass=1.5). Now the lens is submerged in liquid of refractive index 1.42. Find the ratio of focal length in medium to focal length in air has closest value
View SolutionA plano-convex lens has refractive index 1.6 and radius of curvature 60 cm. What is the focal length of the lens?
View SolutionFocal length of a thin convex lens is 30 cm. At distance of 10 cm from the lens there is a plan refracting surface of refractive index 3/2. Where w the parallel rays incident on lens converge ?
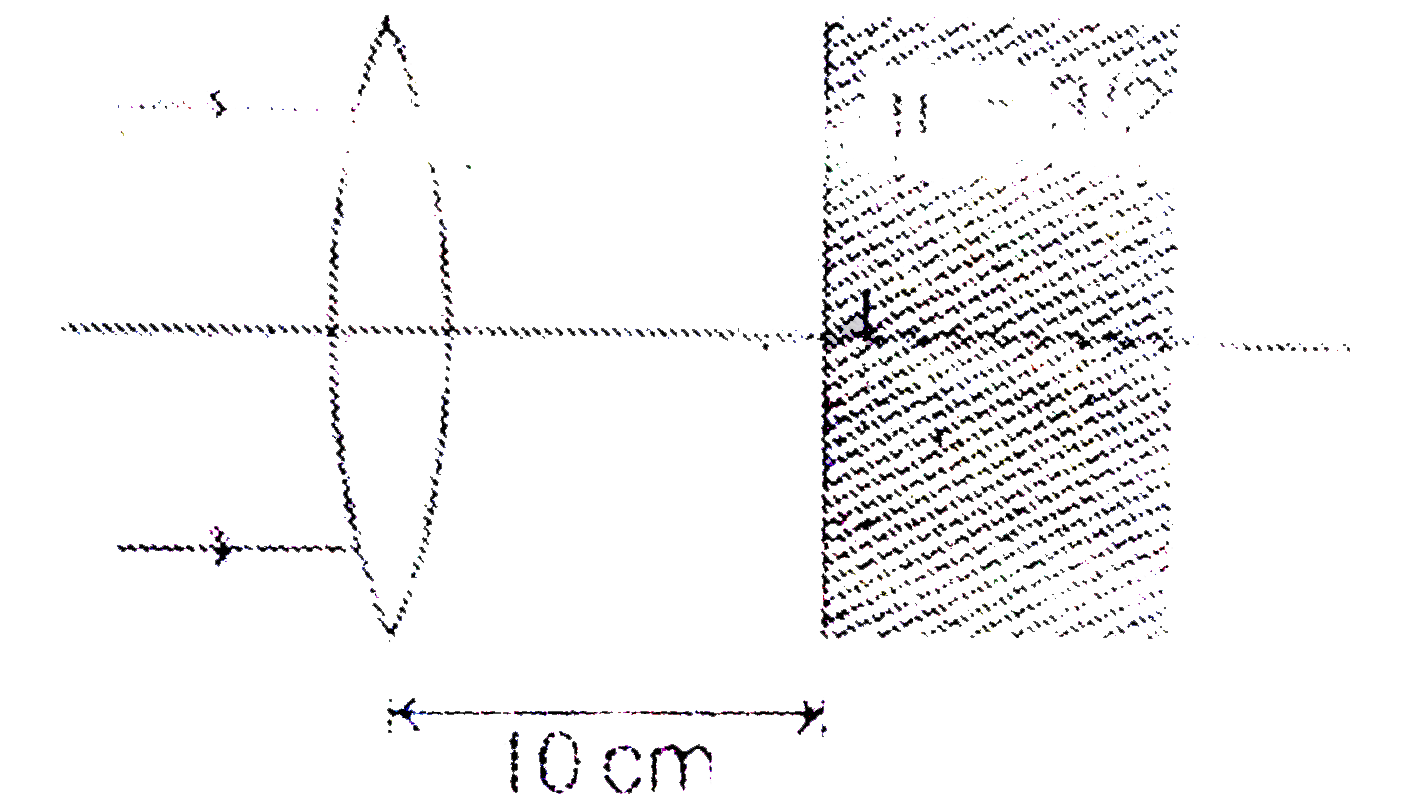 View Solution
View SolutionA focal length of a lens 10cm. What is power of a lens in dipotre?
View SolutionFocal length of a convex lens of refractive index 1.5 is 2 cm. Focal length of lens when immersed in a liquid of refractive index 1.25 will be
View SolutionThe focal length of a thin convex-lens is 30cm. At a distance of 10 cm from the lens there is a plane refracting surface fo refractive inidex 3/2 Where will parallel rays incident on lens converge?
 View Solution
View SolutionA plano-convex lens (focal length f2, refractive indexμ2, radius of curvature R) fits exactly into a plano-concave lens (focal lengthf1 refractive index μ1, radius of curvature R). Their plane surfaces are parallel to each other. Then, the focal length of the combination will be :
View Solution

