Find the focal length of equivalent system shown in Figure.
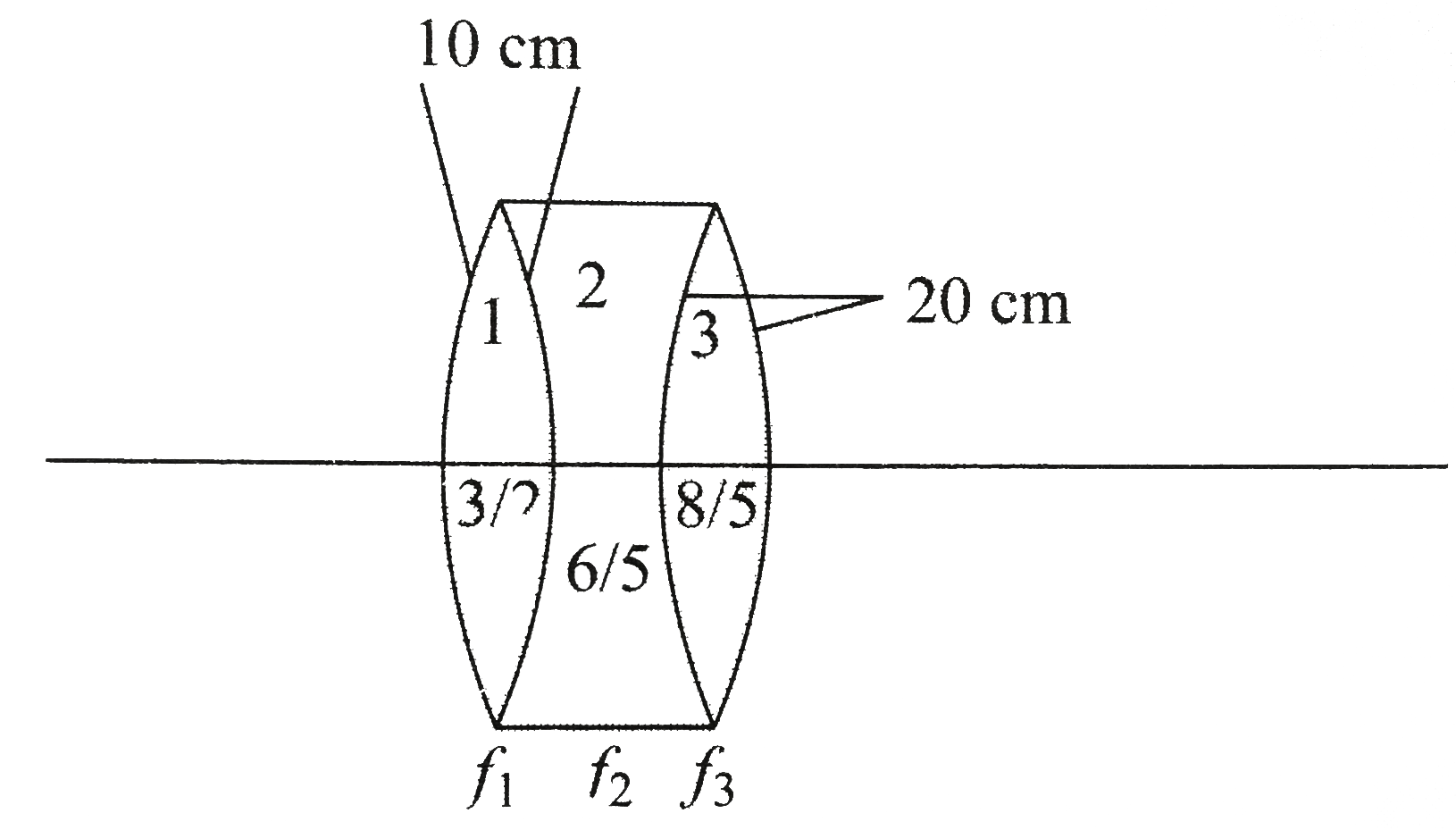
Here radius of curvatures of different surfaces and refractive index are given, we can calculate focal lengths of lenses by using
1f1=(32−1)(110+110)=12×210=110
1f=(μ1−1)(1R1−1R2)
1f2=(65−1)(_110−120)=15×(−3010×20)=−3100
1f3=(85−1)(120+120)=350
Hence, equivalent focal length
1f=1f1+1f2+1f3=110+−3100+350
⇒f=100/13cm
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Solved Examples
15 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.1
14 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
Find the focal length of the lens used.
View SolutionFind the focal length of the lens shown in the Fig..
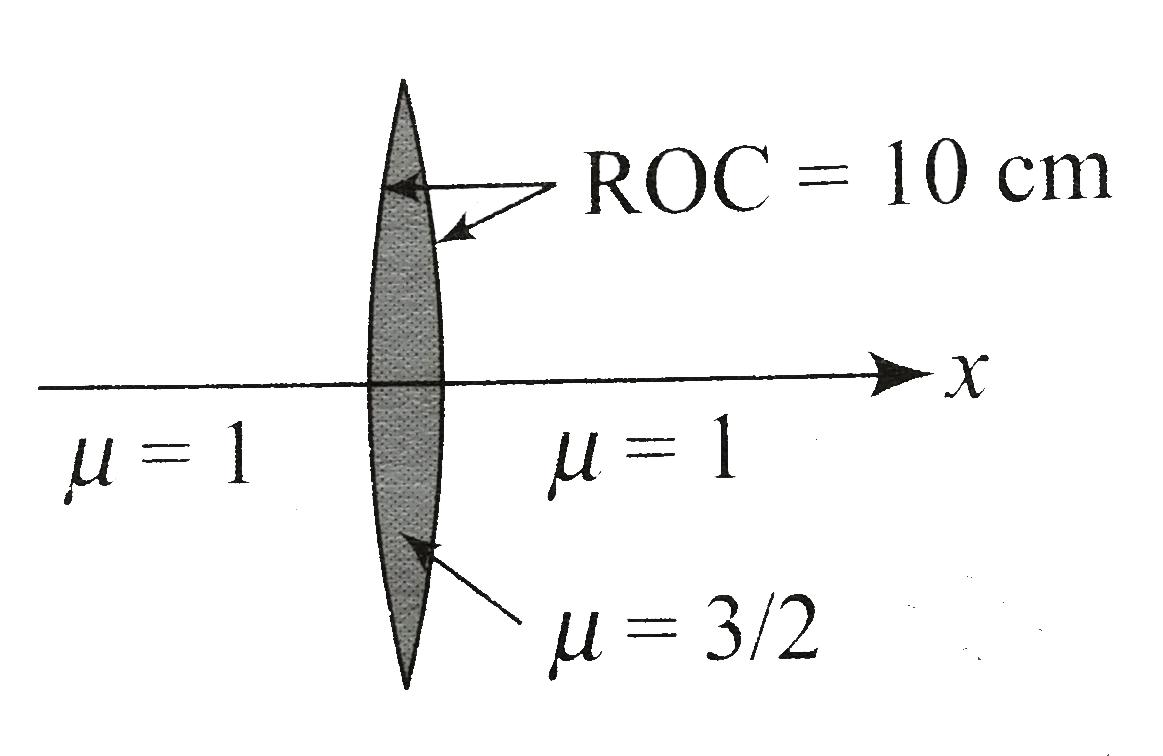
View Solution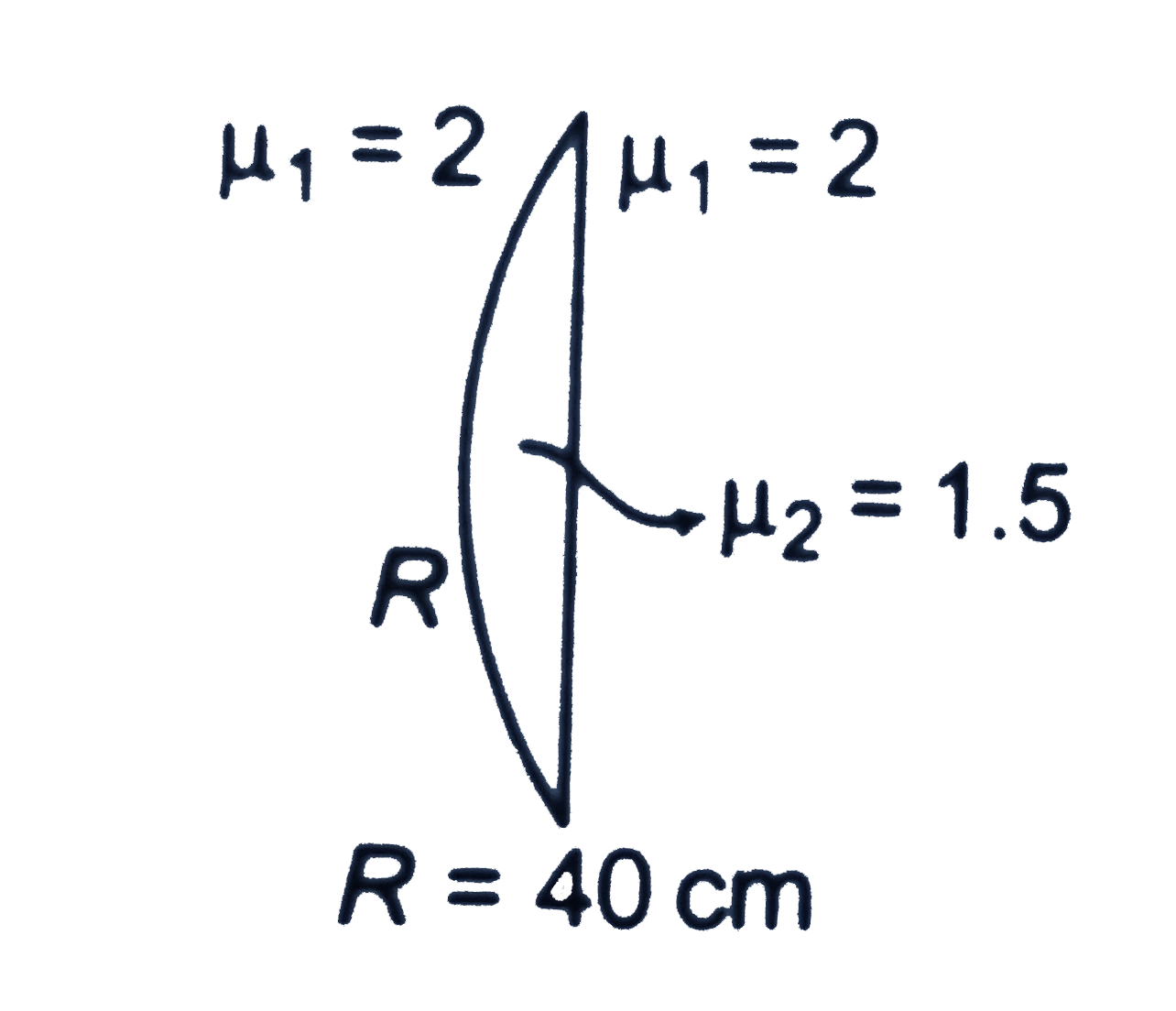
Find focal length of the system shown in figure from left hand side.
View SolutionFind the focal length of the lens shown in Fig . The radii of curvature of both the surfaces are equal to R.
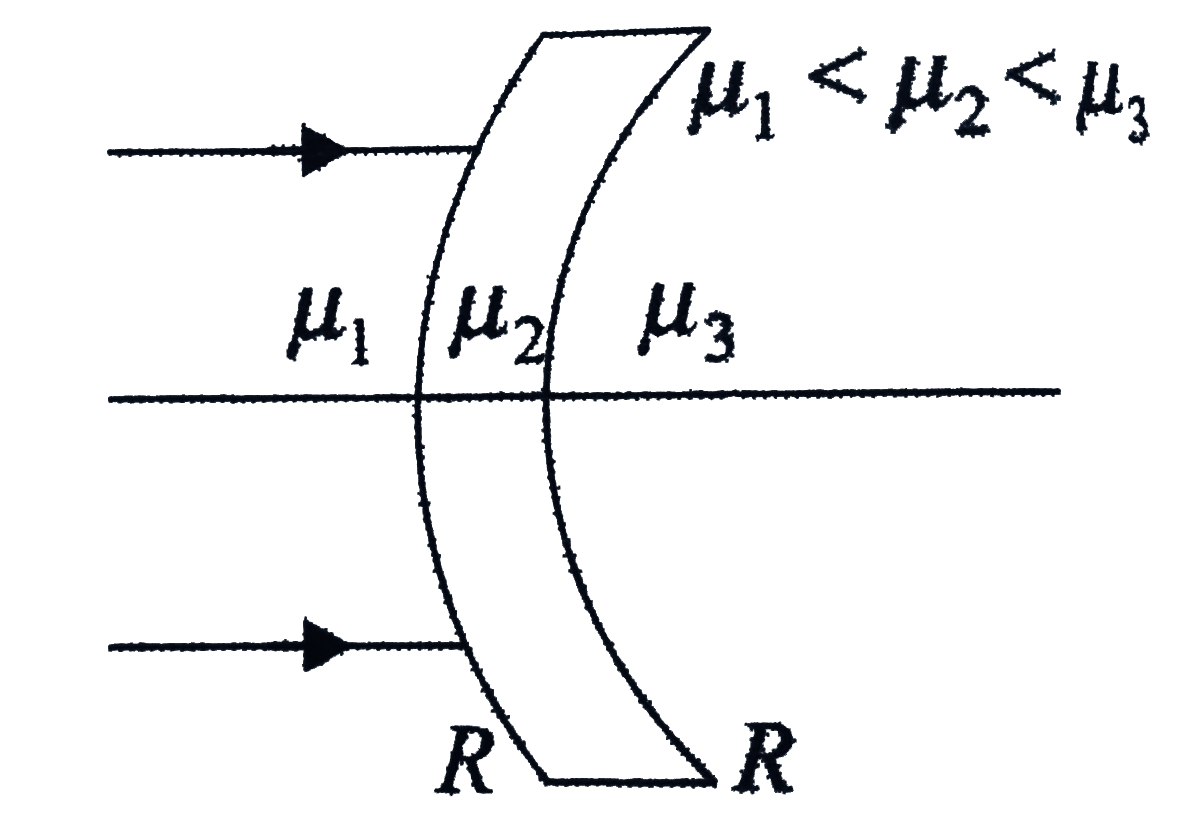
View Solution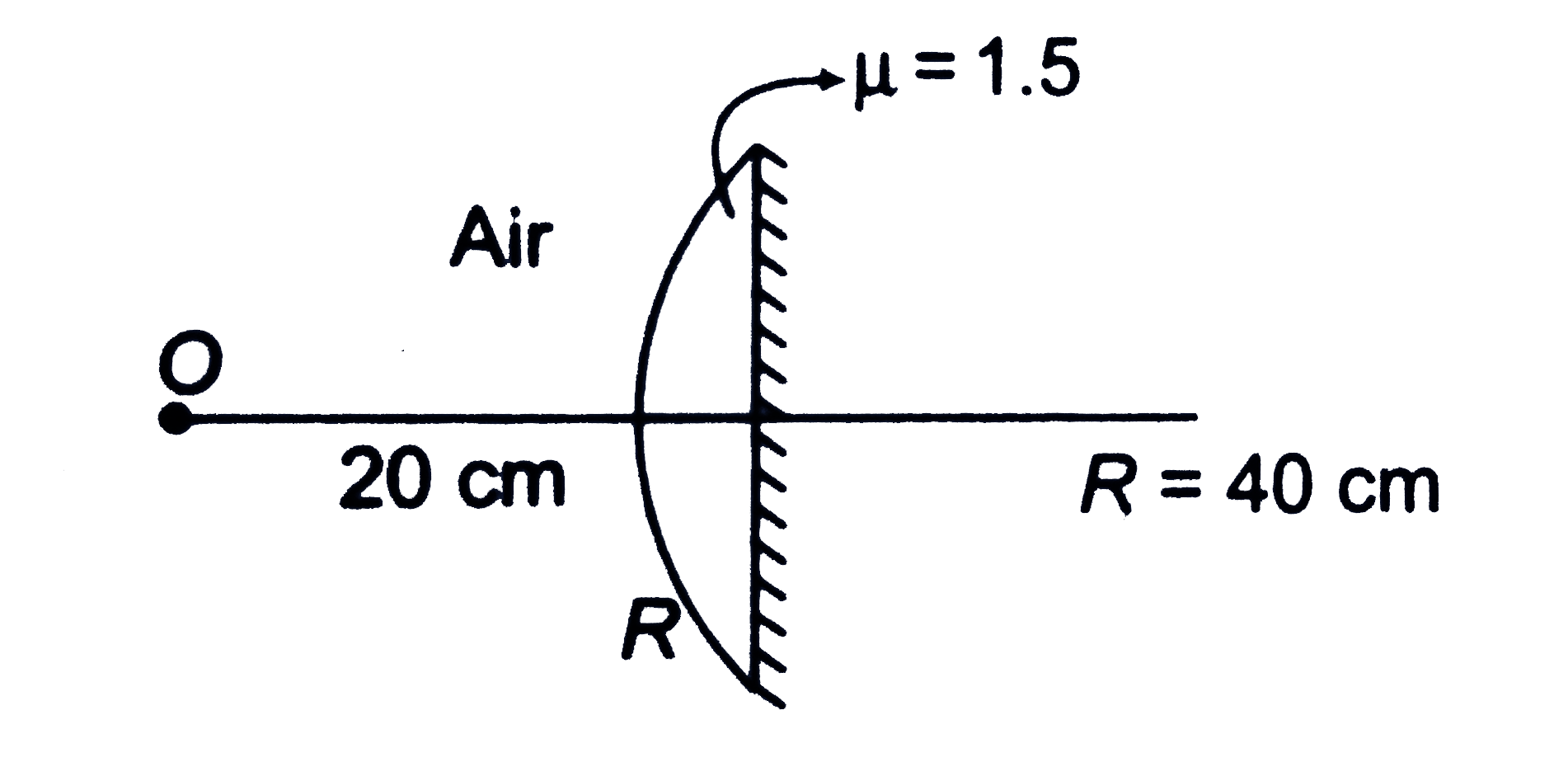
Find focal length of the system as shown if figure.
Find image position.
View SolutionFind the focal length of the lens shown in Fig.
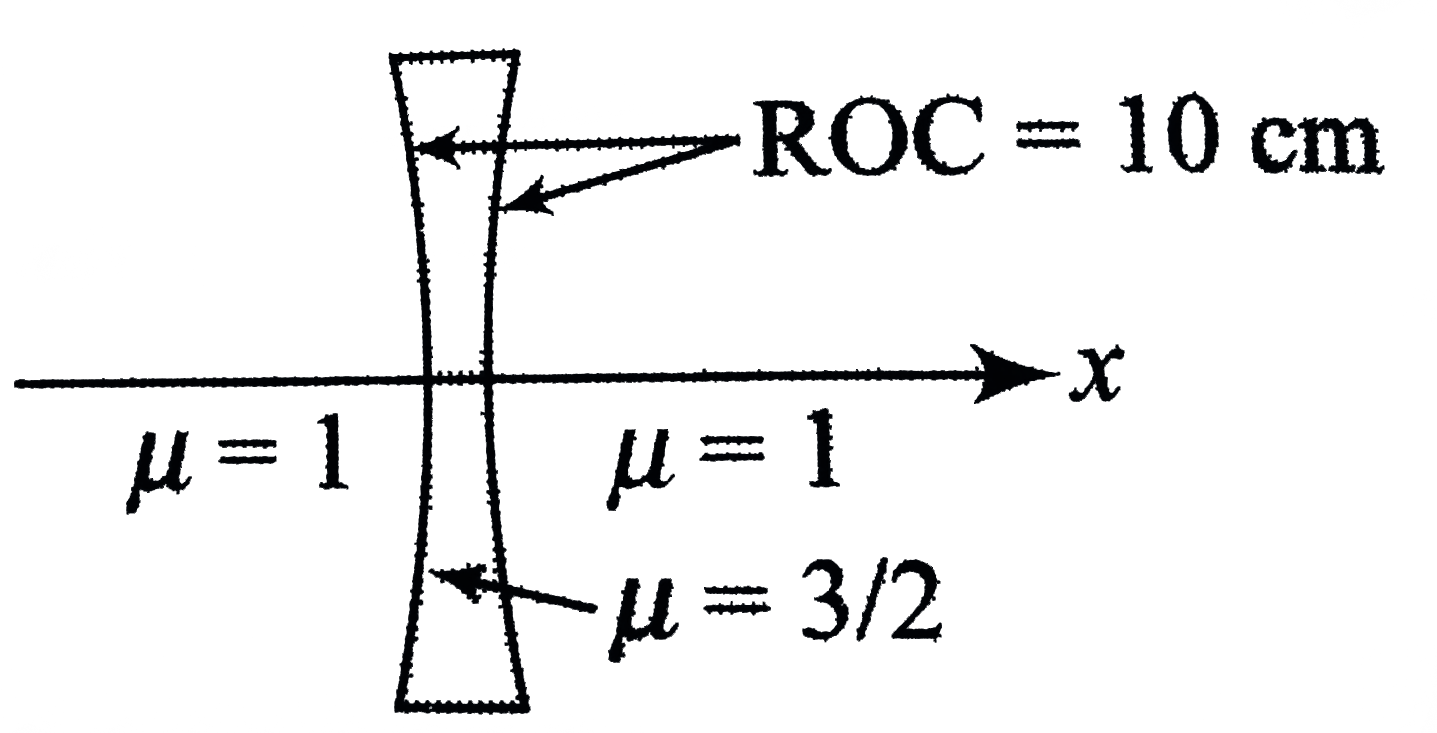
View SolutionFind the natural frequency of the system shown in figure. The pulleys are smooth and massless.

View SolutionFind the period of oscillation of the system shown in figure.

View SolutionFind the electric dipole moment of the system shown in figure.
View SolutionA convex lens of glass (μ=1.5) is formed by combining two surfaces of radii R1=60cm and R2=30cm . It is cut into two parts in two different ways as shown in Figure .
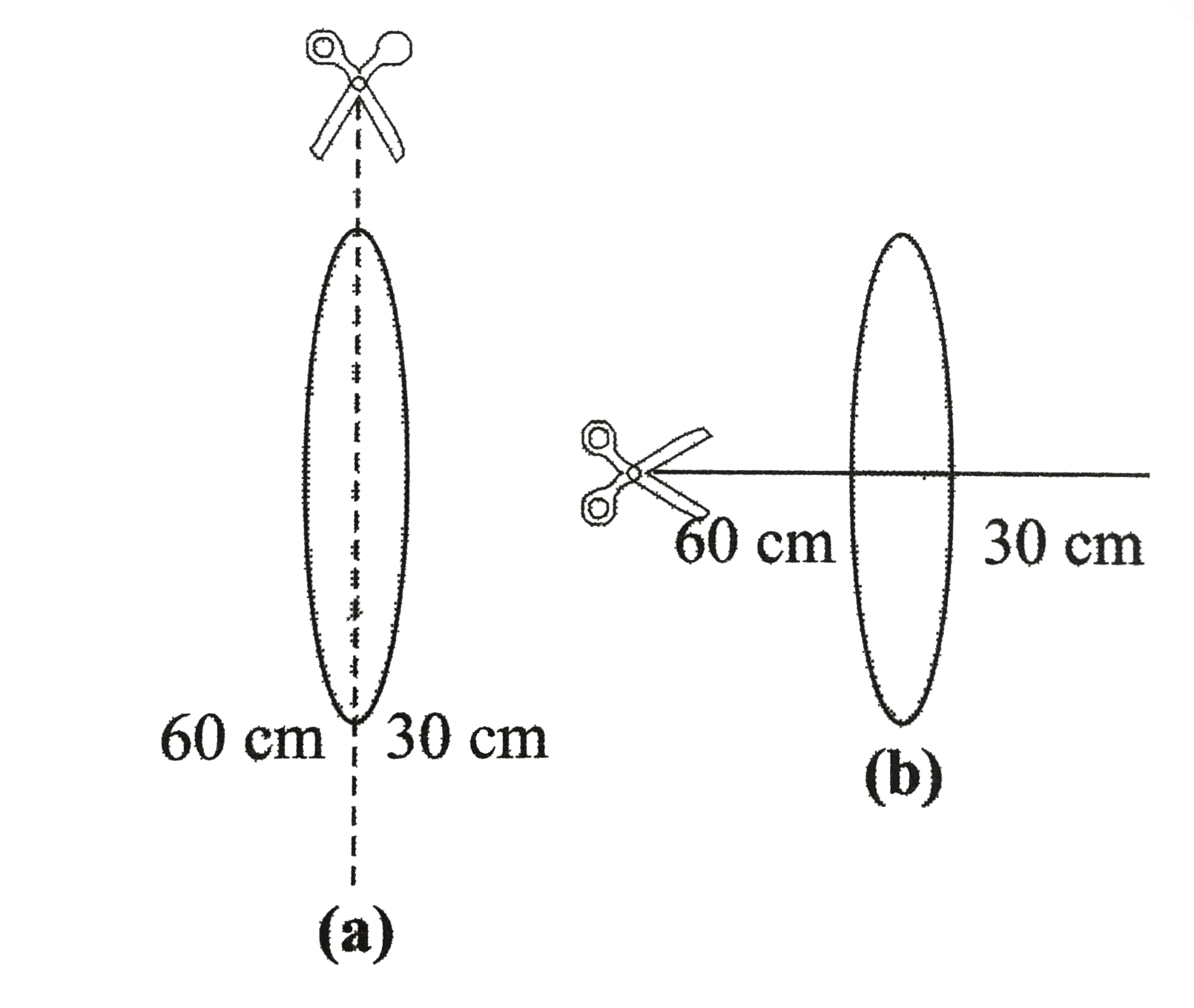
Find:
a. the focal length of the lens.
b. in figure (a), the focal length of left portion and that of the right portion.
c. in figure (b), the focal length of the upper part and that of the lower part.
View Solution
