An object in placed 30cm in front of a concave lens that is made of a glass of refractive index 1.5 and has equal radii of curvature of its two surfaces, each 30 cm. The surface of the lens farther away from the object is silvered. Find the nature and position of the final image.
To solve the problem step by step, we will follow these outlined steps:
Step 1: Identify the parameters of the concave lens
- The object distance (u) = -30 cm (the negative sign indicates that the object is in front of the lens).
- The refractive index (n) of the lens = 1.5.
- The radius of curvature (R) of each surface = 30 cm.
Step 2: Calculate the focal length of the concave lens (F_L)
Using the lens maker's formula:
1FL=(n−1)(1R1−1R2)
For a concave lens, we have:
- R1=−30 cm (the first surface is concave)
- R2=+30 cm (the second surface is convex)
Substituting the values:
1FL=(1.5−1)(1−30−130)
=0.5(−130−130)=0.5(−230)=−130
Thus,
FL=−30 cm
Step 3: Calculate the focal length of the mirror (F_M)
The focal length of a mirror is given by:
FM=R2
For the silvered surface (mirror) with R=30 cm:
FM=302=15 cm
Step 4: Calculate the equivalent focal length of the system (F_eq)
The formula for the equivalent focal length of a system with a lens and a mirror is:
1Feq=1FM−2FL
Substituting the values:
1Feq=115−2−30
=115+115=215
Thus,
Feq=152=7.5 cm
Step 5: Use the mirror formula to find the image distance (v)
The mirror formula is:
1v+1u=1Feq
Substituting u=−30 cm and Feq=7.5 cm:
1v−130=17.5
Calculating 17.5:
17.5=215
Thus,
1v=215+130
Finding a common denominator (30):
1v=430+130=530
Therefore,
v=305=6 cm
Step 6: Determine the nature of the image
Since v is positive, the image is virtual and located 6 cm behind the mirror.
Conclusion
The final image is virtual and located 6 cm behind the mirror.
---
- The object distance (u) = -30 cm (the negative sign indicates that the object is in front of the lens).
- The refractive index (n) of the lens = 1.5.
- The radius of curvature (R) of each surface = 30 cm.
Using the lens maker's formula:
1FL=(n−1)(1R1−1R2)
For a concave lens, we have:
- R1=−30 cm (the first surface is concave)
- R2=+30 cm (the second surface is convex)
1FL=(1.5−1)(1−30−130)
=0.5(−130−130)=0.5(−230)=−130
Thus,
FL=−30 cm
The focal length of a mirror is given by:
FM=R2
For the silvered surface (mirror) with R=30 cm:
FM=302=15 cm
The formula for the equivalent focal length of a system with a lens and a mirror is:
1Feq=1FM−2FL
Substituting the values:
1Feq=115−2−30
=115+115=215
Thus,
Feq=152=7.5 cm
The mirror formula is:
1v+1u=1Feq
Substituting u=−30 cm and Feq=7.5 cm:
1v−130=17.5
Calculating 17.5:
17.5=215
Thus,
1v=215+130
Finding a common denominator (30):
1v=430+130=530
Therefore,
v=305=6 cm
Since v is positive, the image is virtual and located 6 cm behind the mirror.
The final image is virtual and located 6 cm behind the mirror.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Solved Examples15videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.114videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
Similar Questions
A plano-concave lens is made of glass of refractive index 1.5 and the radius of curvature of its curved face is 100 cm. What is the power of the lens?
View SolutionA concavo-convex lens is made of glass of refractive index 1.5. The radii of curvature of its two surfaces are 30cm and 50cm. Its focal length when placed in a liquid of refractive index 1.4 is
View Solution
Knowledge Check
- Question 1 - Select One
A double convex lens made of glass of refractive index 1.56 has both radii of curvature of magnitude 20cm. If an object is placed at a distance of 10cm from this lens, find the position of image formed.
A22.86 same side of the objectB22.86 opposite side of the objectC44.89 same side of the objectD44.89 opposite side of the object.
A biconvex lens is made of glass with refractive index 1.5 and has radii of curvature 20 cm and 30 cm. If the 20 cm surface is silvered, what is the effective focal length of the mirror formed?
 View Solution
View SolutionAn equiconvex lens is made from glass of refractive index 1.5. If the radius of each surface is changed from 5cm to 6cm, then the power
View SolutionA pin is placed 10cm in front of a convex lens of focal length 20cm, made of a material having refractive index 1.5 . The surface of lens farther away from the pin is silvered and has a radius of curvature 22cm. Determine the position of the final image. Is the image real or virtual?
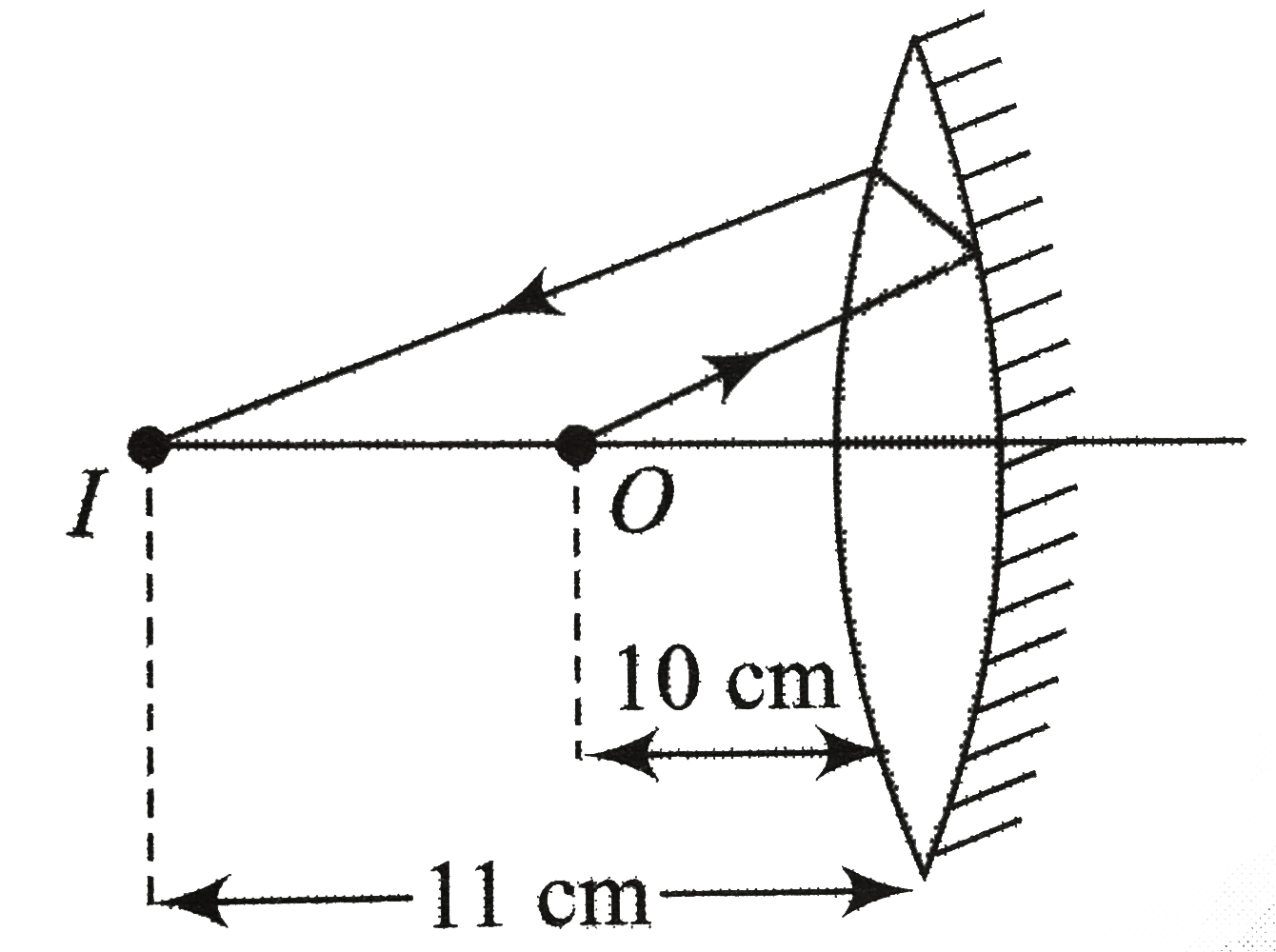 View Solution
View SolutionA double convex thin lens made of glass of refractive index 1.6 has radii of curvature 15 cm each. The focal length of this lens when immersed in a liquid of refractive index 1.63 is :
View SolutionA biconvex lens has radii of curvature 20 cm and 40cm. The refractive index of the material of the lens is 1.5. An object is placed 40cm in front of the lens. Calculate the psition of the image.
View SolutionA convex-concave diverging lens is made of glass of refractive index 1.5 and focal length 24 cm. radius of curvature for one surface is double that of the other. Then radii of curvature for the two surfaces are (in cm )
View SolutionA concavo-convex lens has refractive index 1.5 and the radii of curvature of its surfaces are 10cmand20cm. The concave surface is upwords and is filled with oil of refractive index 1.6. The focal length of the combination will be
View Solution

