A 60 W bulb is placed at a distance of 4 m from you. The bulb is emtting light of wavelength 600 nm uniformly in all directions. In 0.1 s, how many photons enter your eye if the pupil of the eye is having a diameter of 2mm? [take hc=1240eV−nm]
2.84×1012
2.84×1011
9.37×1011
6.48×1011
The correct Answer is:B
To solve the problem step by step, we will follow the outlined procedure to find the number of photons entering the eye from a 60 W bulb emitting light of wavelength 600 nm.
Step 1: Calculate the intensity of light at the distance of the eye
The intensity I of light emitted uniformly from a point source is given by the formula:
I=P4πR2
Where:
- P=60W (power of the bulb)
- R=4m (distance from the bulb)
Substituting the values:
I=604π(4)2=604π⋅16=6064π=1516πW/m2
Step 2: Calculate the area of the pupil of the eye
The area A of the pupil can be calculated using the formula for the area of a circle:
A=π(D2)2
Where:
- D=2mm=2×10−3m
Substituting the value:
A=π(2×10−32)2=π(10−3)2=π×10−6m2
Step 3: Calculate the power entering the eye
The power P1 entering the eye is given by:
P1=I×A
Substituting the values we calculated:
P1=(1516π)×(π×10−6)=15×10−616W
Calculating this gives:
P1=15×10−616=9.375×10−7W
Step 4: Calculate the energy of a single photon
The energy E of a single photon can be calculated using the formula:
E=hcλ
Where:
- h=1240eV-nm
- c=1.6×10−19J/eV
- λ=600nm
Substituting the values:
E=1240×1.6×10−19600=1984×10−19600≈3.3067×10−19J
Step 5: Calculate the number of photons entering the eye per second
The number of photons n entering the eye per second can be calculated using:
P1=n×E
Rearranging gives:
n=P1E
Substituting the values:
n=9.375×10−73.3067×10−19≈2.84×1012photons/second
Step 6: Calculate the number of photons in 0.1 seconds
To find the total number of photons entering the eye in 0.1 seconds:
Total photons=n×0.1=2.84×1012×0.1=2.84×1011photons
Final Answer
The total number of photons entering your eye in 0.1 seconds is approximately 2.84×1011 photons.
---
The intensity I of light emitted uniformly from a point source is given by the formula:
- P=60W (power of the bulb)
- R=4m (distance from the bulb)
The area A of the pupil can be calculated using the formula for the area of a circle:
- D=2mm=2×10−3m
The power P1 entering the eye is given by:
The energy E of a single photon can be calculated using the formula:
- h=1240eV-nm
- c=1.6×10−19J/eV
- λ=600nm
The number of photons n entering the eye per second can be calculated using:
To find the total number of photons entering the eye in 0.1 seconds:
The total number of photons entering your eye in 0.1 seconds is approximately 2.84×1011 photons.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Multiple Correct10videos
PHOTOELECTRIC EFFECT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Linked Comprehension44videos
PHOTOELECTRIC EFFECT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Subjective16videos
PHOTOELECTRIC EFFECT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.514videos
NUCLEAR PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.612videos
RAY OPTICS
Similar Questions
A 100 W sodium lamp is radiating light of wavelength 5890A, uniformly in all directions,
a. At what rate, photons are emitted from the lamp?
b. At what distance from the lamp, the average flux is 1 photon(cm2−s)−1?
c. What are the photon flux and photon density at 2m from the lamp?View SolutionA bulb of 40 W is producing a light of wavelength 620 nm with 80% of efficiency , then the number of photons emitted by the bulb in 20 seconds are :
(1eV=1.6×10−19J,hc=12400eV)View SolutionA sample of hydrogen atom is in excited state (all the atoms ). The photons emitted from this sample are made to pass through a filter through which light having wavelength greater than 800nm can only pass. Only one type of photons are found to pass the filter. The sample's excited state initially is [Takehc=1240eV−nm, ground state energy of hydrogen atom =−13.6eV].
View SolutionA sensor is exposed for 0.1 s to a 200 W lamp 10m away The sensor has an opening that is 20 mm in diameter. How many photons enter the sensor if the wavelength of light is 600nm? Assume that all the energy of the lamp is given off as light.
View SolutionIn Young's double slit experiment , the two slits 0.20 mm apart are illuminated by monochromatic light of wavelength 600 nm . The screen 1.0 m away from the slits .
(a) Find the distance of the second (i) bright fringe , (ii) dark fringe from the central maximum .
(b) How will the fringe pattern change if the screen is moved away from the slits ?View SolutionIn a Young's double slit experiment, a parallel beam containing wavelengths λ1=4000Å and λ2=5600Å is incident at an angle ϕ=30∘ on a diaphragm having narrow slits at separation d=2mm. The screen is placed at a distance D =40 cm from the slits. a mica slab of thickness t=5mm is placed in front of one of the slits and whole of the apparatus is submerged in water. if the central bright fringe is observed at C, determine.

(i) The refractive index of the slab
(ii) The distance of first black line from C
both wavelength are in air. take μw=43View SolutionThe path of photoelectrons emitted due to electromagnetic radiation incident on a sample of material A, is found to have a maximum bending radius of 0.1 m in a magnetic field of (√23)×10−4T. When the radiation is incident normally on a double slit having a slit separation of 0.1mm, it is observed that there are 10 fringes in a width of 3.1 cm on a screen placed at a distance of 1 m from the double slit. Find the work function of the material. and the corresponding threshold wavelength. What sould be the wavelength of the incident light so that the bending radius is one-half of what it was before? Given that mass of the electron=0.5MeVc2,hc=12400eV−A
View SolutionA point source of monochromatic light of 1.0mW is placed at a distance of 5.0m from a metal surface. Light falls perpendicularly on the surface. Assume wave theory of light to hold and also that all the light falling on the circular area with radius =1.0×10−9m(which is few times the diameter of an atom) is absorbed by a single electron on the surface. Calculate the time required by the electron to receive sufficient energy to come out of the metal if the work function of the metal is 2.0eV.
View SolutionIn a Young's double slit experiment, the light sources is at distance l1=20μm and l2=40μm form the main slit. The light of wavelength lambda = 500nm is incident on slits separated at a distance 10μm. A screen is placed at a distance D = 2 away from the slits as shown in figure. Find
(a) the values of θ relative to the central line where maxima appear on the screen?
(b) how many maxima will appear on the screen?
what should be the minimum thickness of a slab of refractive index 1.5 placed on the path of one of the ray so that minima occurs at C ?
 .View Solution
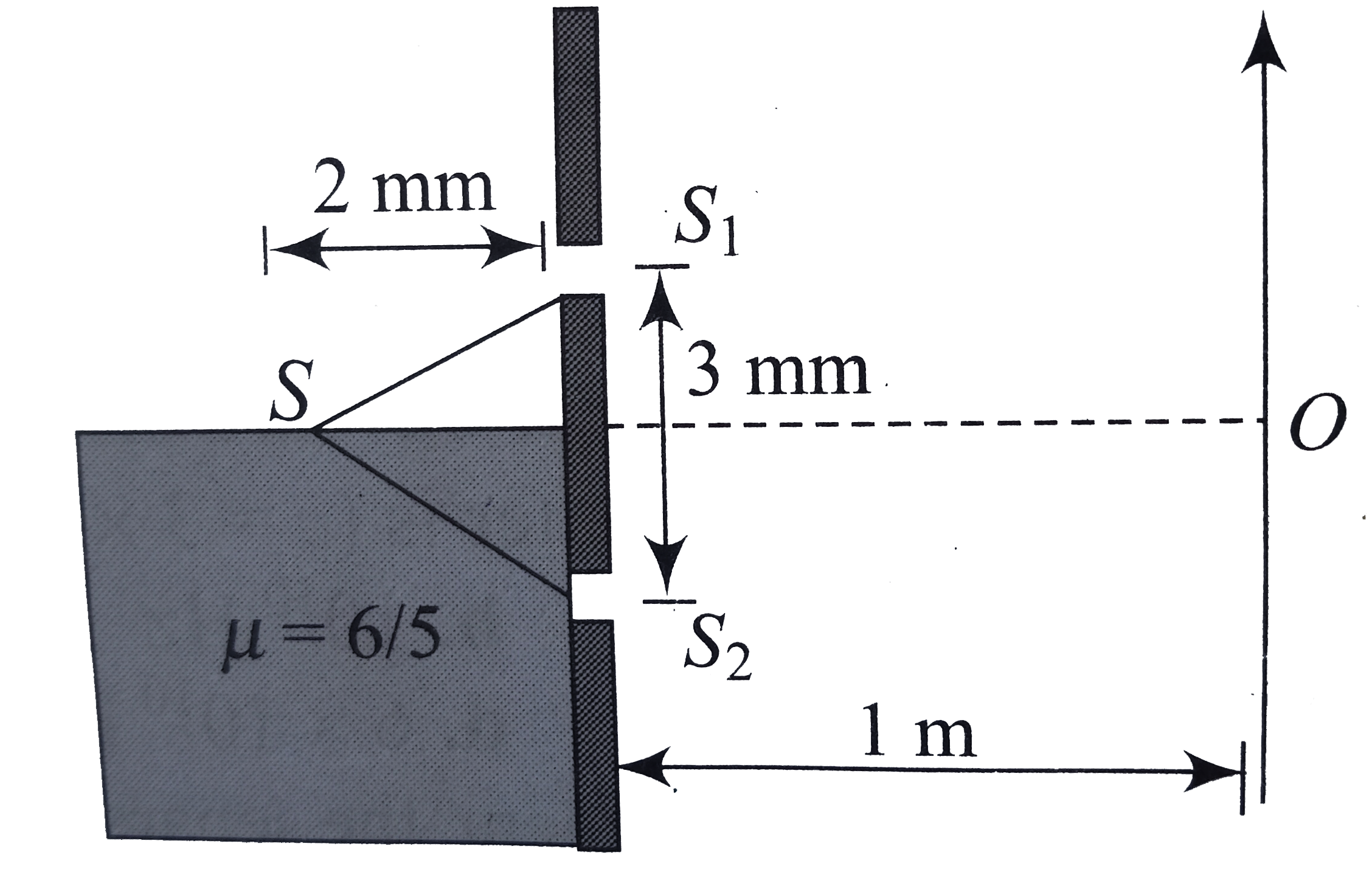
.View SolutionIn Young's double-slit experiment, a point source is placed on a solid slab of refractive index 6/5 at a distance of 2 mm from two slits spaced 3 mm apart as shown and at equal distacne from both the slits. The screen is at a distance of 1 m from the slits. Wavelength of light used is 500 nm.
a. Find the position of the central maximum.
b. Find the order of the fringe formed at O.
c. A film of refractive index 1.8 is to be placed in front of S1 so that central maxima is formed where 200th maxima was formed. Find the thickness of film.
 View Solution
View Solution

