Light of intensity I falls along the axis on a perfectly refleccting right circular cone having semi-vertical angle θ and base radius R. If E is the energy of one photon and c is the speed oh light, then find
Q. The net force of the cone.
(πR2I)(1−cos2θ)c
(πR2I)2c(1−cos2θ)
2(πR2I)c(1−cos2θ)
(πR2I)2c(1+cos2θ)
The correct Answer is:A
To solve the problem, we need to find the net force exerted on a perfectly reflecting right circular cone when light of intensity I falls on it. Here are the steps to derive the solution:
Step 1: Understand the Geometry of the Cone
The cone has a semi-vertical angle θ and a base radius R. The light is falling along the axis of the cone, which means it is directed vertically downwards. The angle of incidence with respect to the normal at the surface of the cone will be 90∘−θ.
Step 2: Calculate the Projected Area
The projected area A of the cone's base that is illuminated by the light is given by:
A=πR2
Step 3: Relate Intensity to Energy
The intensity I of the light is defined as the power per unit area. Therefore, the total power P incident on the cone can be expressed as:
P=I⋅A=I⋅πR2
Step 4: Determine the Energy of a Single Photon
Let E be the energy of a single photon. The number of photons N striking the cone per second can be calculated using the relationship between power and energy:
N=PE=I⋅πR2E
Step 5: Change in Momentum for a Photon
When a photon strikes a perfectly reflecting surface, it undergoes a change in momentum. The change in momentum Δp for a single photon is given by:
Δp=2Ec
where c is the speed of light.
Step 6: Calculate the Force Exerted by Photons
The force F exerted by a single photon can be expressed as the rate of change of momentum:
F=N⋅Δp=N⋅2Ec
Substituting N from Step 4:
F=(I⋅πR2E)⋅2Ec=2πR2Ic
Step 7: Consider the Angle of Reflection
Since the cone reflects the photons, we need to account for the angle θ. The vertical component of the force will be:
Fnet=F⋅sin(θ)
However, since the cone is symmetric, we consider the vertical component of the force:
Fnet=2πR2Ic⋅sin2(θ)
Step 8: Final Expression
Using the identity sin2(θ)=1−cos(2θ)2, we can express the net force as:
Fnet=πR2Ic(1−cos(2θ))
Conclusion
The net force on the cone is given by:
Fnet=πR2Ic(1−cos(2θ))
The cone has a semi-vertical angle θ and a base radius R. The light is falling along the axis of the cone, which means it is directed vertically downwards. The angle of incidence with respect to the normal at the surface of the cone will be 90∘−θ.
The projected area A of the cone's base that is illuminated by the light is given by:
A=πR2
The intensity I of the light is defined as the power per unit area. Therefore, the total power P incident on the cone can be expressed as:
P=I⋅A=I⋅πR2
Let E be the energy of a single photon. The number of photons N striking the cone per second can be calculated using the relationship between power and energy:
N=PE=I⋅πR2E
When a photon strikes a perfectly reflecting surface, it undergoes a change in momentum. The change in momentum Δp for a single photon is given by:
Δp=2Ec
where c is the speed of light.
The force F exerted by a single photon can be expressed as the rate of change of momentum:
F=N⋅Δp=N⋅2Ec
Substituting N from Step 4:
F=(I⋅πR2E)⋅2Ec=2πR2Ic
Since the cone reflects the photons, we need to account for the angle θ. The vertical component of the force will be:
Fnet=F⋅sin(θ)
However, since the cone is symmetric, we consider the vertical component of the force:
Fnet=2πR2Ic⋅sin2(θ)
Using the identity sin2(θ)=1−cos(2θ)2, we can express the net force as:
Fnet=πR2Ic(1−cos(2θ))
The net force on the cone is given by:
Fnet=πR2Ic(1−cos(2θ))
Topper's Solved these Questions
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Integer
9 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Single Correct Answer Type
7 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Multiple Correct
10 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.5
14 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
Similar Questions
Light of intensity I falls along the axis on a perfectly reflecting right circular cone having semi-vertical angle θ and base radius R. If E is the energy of one photon and c is the speed oh light, then find
the number of photons hitting the cone per second
View SolutionThe radius of the base of a right circular cone of semi-vertical angle α is r . Show that its volume is 13πr3 cotα and curved surface area is πr2 coses α.
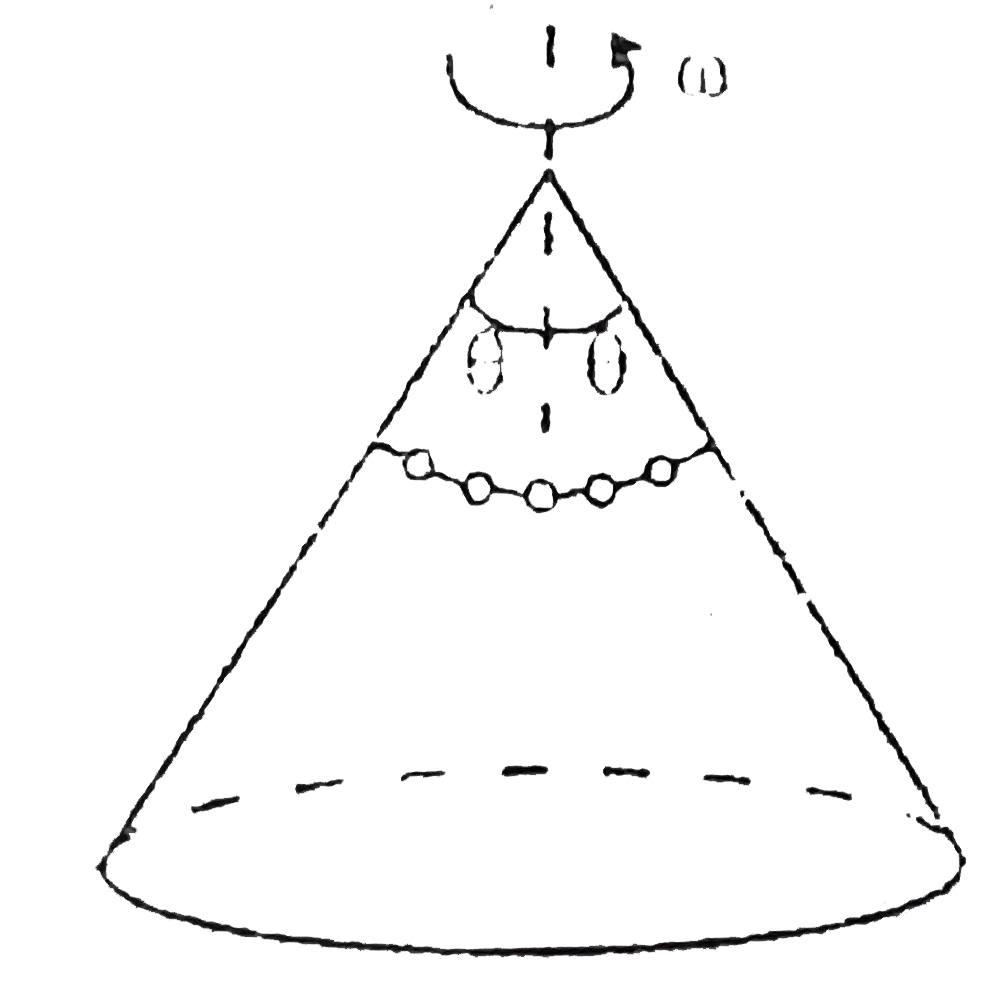
View SolutionA chain of mass 'm' and radius 'r' is placed onto a cone of semi vertical angle θ. Cone rotated with angular velocity ω. Find the tension in the chain if it does not slide on the cone.
View SolutionQ charge is uniformaly distributed over the same surface of a right circular cone of semi -vertical angle theta and height h The cone is uniformly rotated about its axis at angular velocity omega Calculated associated magnetic dipole moment
 .
.
View SolutionA water tank has the shape of an inverted right circular cone with its axis vertical and vertex lowermost. Its semi-vertical angle is tan−1(0.5) . Water is poured into it at a constant rate of 5 cubic metre per hour. Find the rate at which
View SolutionAn electron & a photon have same energy E. Find the ratio of de Broglie wavelength of electron to wavelength of photon. Given mass of electron is m & speed of light is C
View SolutionAn electron & a photon have same energy E. Find the ratio of de Broglie wavelength of electron to wavelength of photon. Given mass of electron is m & speed of light is C
View SolutionA water tank has the shape of an inverted right circular cone with its axis vertical and vertex lowermost. Its semi-vertical angle is tan−1(0.5). Water is poured into it at a constant rate of 5 cubic metre per hour. Find the rate at which the level of the water is rising at the instant when the depth of water in the tank is 4m.
View SolutionThe Betatron was the first important machine for producing high energy electrons. The action of the betatron depends on the same fundamental principle as that of the transformer in which an alternating current applied to a primary coil induces an altermating current usually with higher or lower voltage in the secondary coil. In the betatron secondary coil is replaced by a doughnut shaped vacuum chamber.Electron produced in the doughnut from a hot filament, are given a preliminary acceleration by the application of an electric field having potential difference of 20kV to 70kV, when an alternating magnetic field is applied parallel to the axis of the tube, two effects are produced (1) an electromotive force is produced in the electron orbit by the changing magnetic flux that gives an additional energy to the electrons (2) a radial force is produced by the action of magnetic field whose direction is perpendicular to the electron velocity. Which keeps the electron moving in a circular path. Conditions are arranged such that the increasing magnetic field keeps the electron in a circular orbit of constant radius. The mathematical relation between the betatron parameters to ensure the above condition is called BETATRON condition.
If the orbit radius of the circular path traced by the electron is R, magnetic field is B, speed of the electron is v, mass of the electron is m, charge on the electron is e and ϕ is the flux within the orbit of radius R. Then answer the following questions based on the above comprehension.
What is the tangential force acting on the electron ?
View SolutionTwo identical balls AandB eavh of mass 0.1kg are attached to two identical mass less is springs. The spring-mass system is consetrained to move inside a right smooth pipe bent in the form of a circle as shown in figure . The pipe is fixed in a horigental plane. The center of the balls can move in a circle of radius 0.06m. Each spring has a natural length of 0.06πm and force constant 0.1N/m. Initially, both the balls are displaced bu an angle θ=π/6 dadius withrespect to diameter PQ of the circle and released from rest.
a. Calculate the frequency of oscillation of the ball B.
b. What is the total energy of the system ?
c. Find the speed of the bal A when A and B are at the two ends of the diameter PQ.

View Solution
