Suppose that means were available for stripping 28 electrons from _29Cu in vapour of this metel.
a. Compute the first three energy level for the remaining electron.
b. Find the wavelength of the spectral line of the series for which n1=1,n2=3,4. What is the ionization potential for the last electron?
To solve the problem step by step, we will follow the instructions given in the question.
Part (a): Compute the first three energy levels for the remaining electron.
1. Identify the Atomic Number (Z):
The atomic number of Copper (Cu) is 29. After stripping 28 electrons, we are left with 1 electron, making it a hydrogen-like atom.
2. Use the Formula for Energy Levels:
The energy levels for a hydrogen-like atom can be calculated using the formula:
En=−13.6eV⋅Z2n2
where En is the energy of the level, Z is the atomic number, and n is the principal quantum number.
3. Calculate the Energy Levels:
- For n=1:
E1=−13.6⋅29212=−13.6⋅8411=−11437.6eV
- For n=2:
E2=−13.6⋅29222=−13.6⋅8414=−2859.4eV
- For n=3:
E3=−13.6⋅29232=−13.6⋅8419=−1270.8eV
4. Summary of Energy Levels:
- E1=−11437.6eV
- E2=−2859.4eV
- E3=−1270.8eV
Part (b): Find the wavelength of the spectral lines for n1=1, n2=3 and n2=4.
1. Calculate the Wavelength for n2=3:
- The energy difference ΔE when an electron transitions from n=3 to n=1 is:
ΔE=E3−E1=−1270.8−(−11437.6)=10166.8eV
- The wavelength λ can be calculated using:
λ=1240nm⋅eVΔE
- Substituting the values:
λ1=124010166.8≈0.121nm or 1.21Å
2. Calculate the Wavelength for n2=4:
- The energy difference ΔE when an electron transitions from n=4 to n=1 is:
ΔE=E4−E1=−714.85−(−11437.6)=10722.75eV
- The wavelength λ can be calculated using:
λ2=124010722.75≈0.115nm or 1.15Å
3. Summary of Wavelengths:
- Wavelength for n2=3: λ1≈0.121nm
- Wavelength for n2=4: λ2≈0.115nm
Ionization Potential for the Last Electron:
1. Calculate Ionization Potential:
- The ionization potential is the energy required to remove the last electron from its ground state:
Ionization Potential=E∞−E1
- Since E∞=0:
Ionization Potential=0−(−11437.6)=11437.6eV
Final Answers:
- First three energy levels:
- E1=−11437.6eV
- E2=−2859.4eV
- E3=−1270.8eV
- Wavelengths:
- λ1≈0.121nm
- λ2≈0.115nm
- Ionization Potential: 11437.6eV
The atomic number of Copper (Cu) is 29. After stripping 28 electrons, we are left with 1 electron, making it a hydrogen-like atom.
The energy levels for a hydrogen-like atom can be calculated using the formula:
En=−13.6eV⋅Z2n2
where En is the energy of the level, Z is the atomic number, and n is the principal quantum number.
- For n=1:
E1=−13.6⋅29212=−13.6⋅8411=−11437.6eV
- For n=2:
E2=−13.6⋅29222=−13.6⋅8414=−2859.4eV
- For n=3:
E3=−13.6⋅29232=−13.6⋅8419=−1270.8eV
- E1=−11437.6eV
- E2=−2859.4eV
- E3=−1270.8eV
- The energy difference ΔE when an electron transitions from n=3 to n=1 is:
ΔE=E3−E1=−1270.8−(−11437.6)=10166.8eV
- The wavelength λ can be calculated using:
λ=1240nm⋅eVΔE
- Substituting the values:
λ1=124010166.8≈0.121nm or 1.21Å
- The energy difference ΔE when an electron transitions from n=4 to n=1 is:
ΔE=E4−E1=−714.85−(−11437.6)=10722.75eV
- The wavelength λ can be calculated using:
λ2=124010722.75≈0.115nm or 1.15Å
- Wavelength for n2=3: λ1≈0.121nm
- Wavelength for n2=4: λ2≈0.115nm
- The ionization potential is the energy required to remove the last electron from its ground state:
Ionization Potential=E∞−E1
- Since E∞=0:
Ionization Potential=0−(−11437.6)=11437.6eV
- First three energy levels:
- E1=−11437.6eV
- E2=−2859.4eV
- E3=−1270.8eV
- Wavelengths:
- λ1≈0.121nm
- λ2≈0.115nm
- Ionization Potential: 11437.6eV
Topper's Solved these Questions
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Exercise 4.2
12 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Subject
17 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Solved Examples
23 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Single Correct
10 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
Similar Questions
The energy levels of a hypotherical one electron atom are shown in figure

Find the short wavelength limit of the series terminating at n=2.
View SolutionCalculate the wavelength of the spectral line when an electron jumps from n=7 to n=4 level in an atom of hydrogen.
View SolutionThe wavelength of the spectral line when the electron is the hydrogen atom undergoes a transition from the energy level 4 to energy level 2 is.
View SolutionThe energy levels of a hypotherical one electron atom are shown in figure
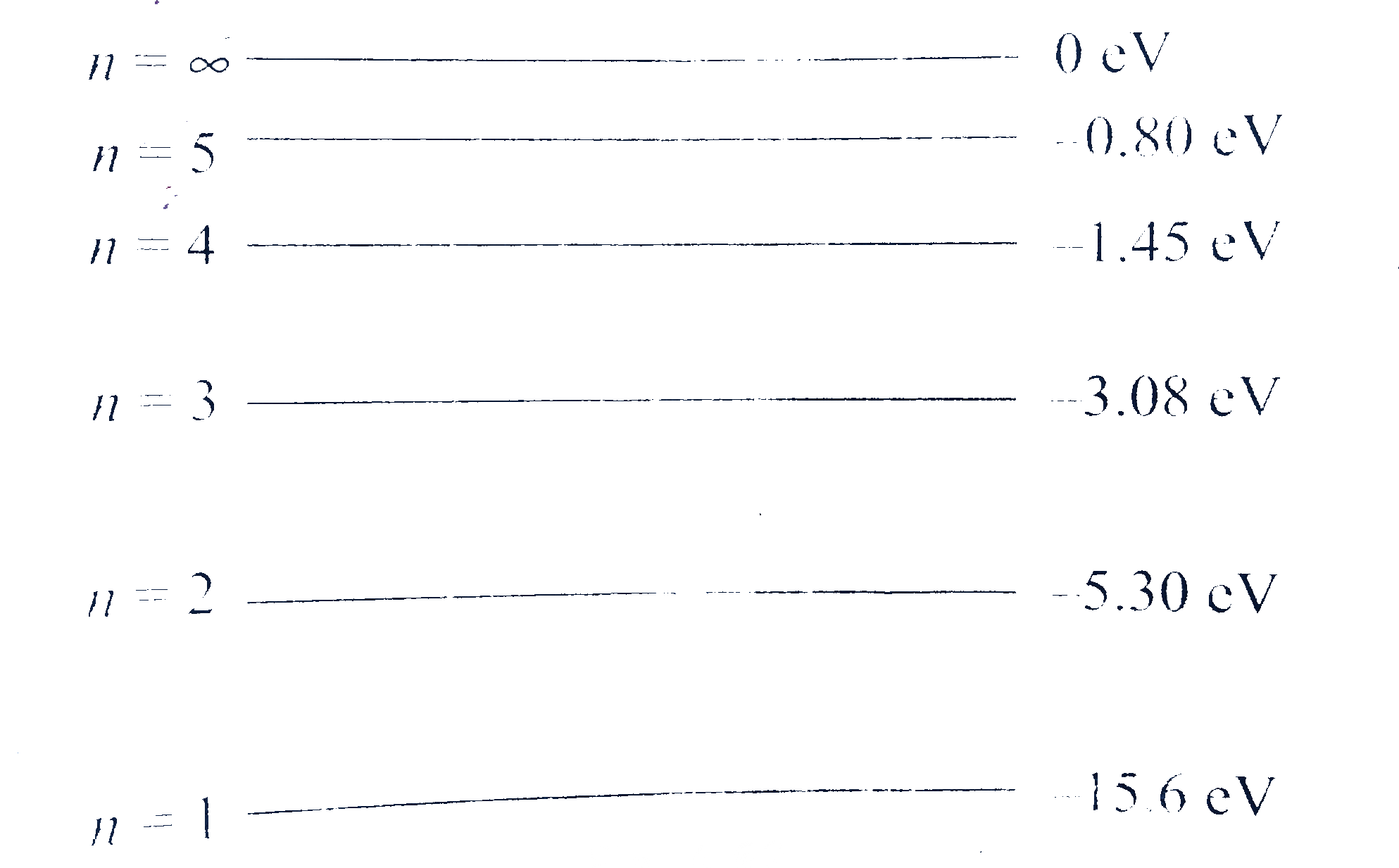
Find the wave number of the photon emitted for the transition n=3→n=1
View SolutionAn electron in H -atoms jumps from some higher level to 3rd energy level.If three spectral lines are possible for the transition, find the initial position of electron.
View SolutionA line in Lyman series of hydrogen atom has a wavelength of 1.03×10−7m . What is the initial energy level of the electron ?
View SolutionFor a certain hypothetical one electron atom, the wavelength (∈Å) for the spectral lines for transitions originating at n=p and terminating at n=1 are given by λ=1500p2p2−1,wherep=2,3,4
(a)Find the wavelength of the least energetic and the most energetic photons in this series.
(b) Construct an energy level diagram for this element showing the energies of the lowest three levels.
(c ) What is the ionization potential fo this elelment?
View SolutionWhen the electron in an excited hydrogen atom jumps from an energy level for which n=5 to level for which n=2 ,the spectral line is obeserved in which series of the hydrogen spectrum?
View SolutionBrackett series of lines are producted when electrons excited t high energy level make transitions to the n=4 level.
a Determine the longest wavelength in this series.
b Determine the wavelength that corresponds to the transition from nf=6→ni=4.
View SolutionElectrons in a certain energy level n=n1 can emit 3 spectral lines. When they are in another energy level, n=n2, they can emit 6 spectral lines. The orbital speed of the electrons in the two orbits are in the ratio
View Solution
