A beam of electron accelerated by a large potential difference V is mode of strike a metal target of produce X-ray . For what value of V , will the resulting X-ray have the lower minimum wavelength?
The correct Answer is:D
To solve the problem of finding the potential difference V that results in the minimum wavelength of X-rays produced when a beam of electrons strikes a metal target, we can follow these steps:
1. Understanding the Relationship Between Energy and Wavelength:
The energy E of a photon is related to its wavelength λ by the equation:
E=hcλ
where h is Planck's constant and c is the speed of light.
2. Relating Energy to Potential Difference:
When electrons are accelerated through a potential difference V, they gain kinetic energy equal to the work done on them by the electric field:
E=eV
where e is the charge of an electron.
3. Combining the Equations:
By equating the two expressions for energy, we have:
eV=hcλ
Rearranging this gives us the wavelength in terms of the potential difference:
λ=hceV
4. Finding the Minimum Wavelength:
From the equation λ=hceV, we can see that the wavelength λ is inversely proportional to the potential difference V. This means that to minimize λ, we need to maximize V.
5. Choosing the Maximum Potential Difference:
Given multiple options for the potential difference V, we need to select the largest value to achieve the minimum wavelength.
6. Identifying the Correct Option:
If the options provided are:
- Option 1: 20 kV
- Option 2: 30 kV
- Option 3: 35 kV
- Option 4: 40 kV
The largest potential difference is 40 kV.
Conclusion:
Thus, the value of V that will result in the minimum wavelength of the X-rays produced is:
40 kV
The energy E of a photon is related to its wavelength λ by the equation:
E=hcλ
where h is Planck's constant and c is the speed of light.
When electrons are accelerated through a potential difference V, they gain kinetic energy equal to the work done on them by the electric field:
E=eV
where e is the charge of an electron.
By equating the two expressions for energy, we have:
eV=hcλ
Rearranging this gives us the wavelength in terms of the potential difference:
λ=hceV
From the equation λ=hceV, we can see that the wavelength λ is inversely proportional to the potential difference V. This means that to minimize λ, we need to maximize V.
Given multiple options for the potential difference V, we need to select the largest value to achieve the minimum wavelength.
If the options provided are:
- Option 1: 20 kV
- Option 2: 30 kV
- Option 3: 35 kV
- Option 4: 40 kV
Thus, the value of V that will result in the minimum wavelength of the X-rays produced is:
40 kV
Topper's Solved these Questions
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Multiple Correct
13 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Linked Comprehension
62 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Subject
17 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Single Correct
10 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
Similar Questions
A beam of electron accelerated by a large potential difference V is mode of strike a metal target of produce X-ray . For which of the following value of V , will the resulting X-ray have the lower minimum wavelength?
View SolutionAn electron is accelerated by a potential difference of 25 V. Find the de Broglie wavelength associated with it.
View SolutionAn electron is accelerated by a potential difference of 50 V. Find the de Broglie wavelength associated with it.
View SolutionAn electron beam is acceleration by a potential difference V to hit a metallic target to produce X-rays. It produces continuous as well as characteristic X-rays. If λmin is the smallest possible wavelength of X-rays in the spectrum, the variation of logλmin with logv is correctly represented in
View Solutionde Broglie wavelength of an electron after being accelerated by a potential difference of V volt from rest is :
View SolutionAn electron is accelerated by a potential difference of 9.375 V . Find the de-Broglie wavelength associated with it is Å
View Solution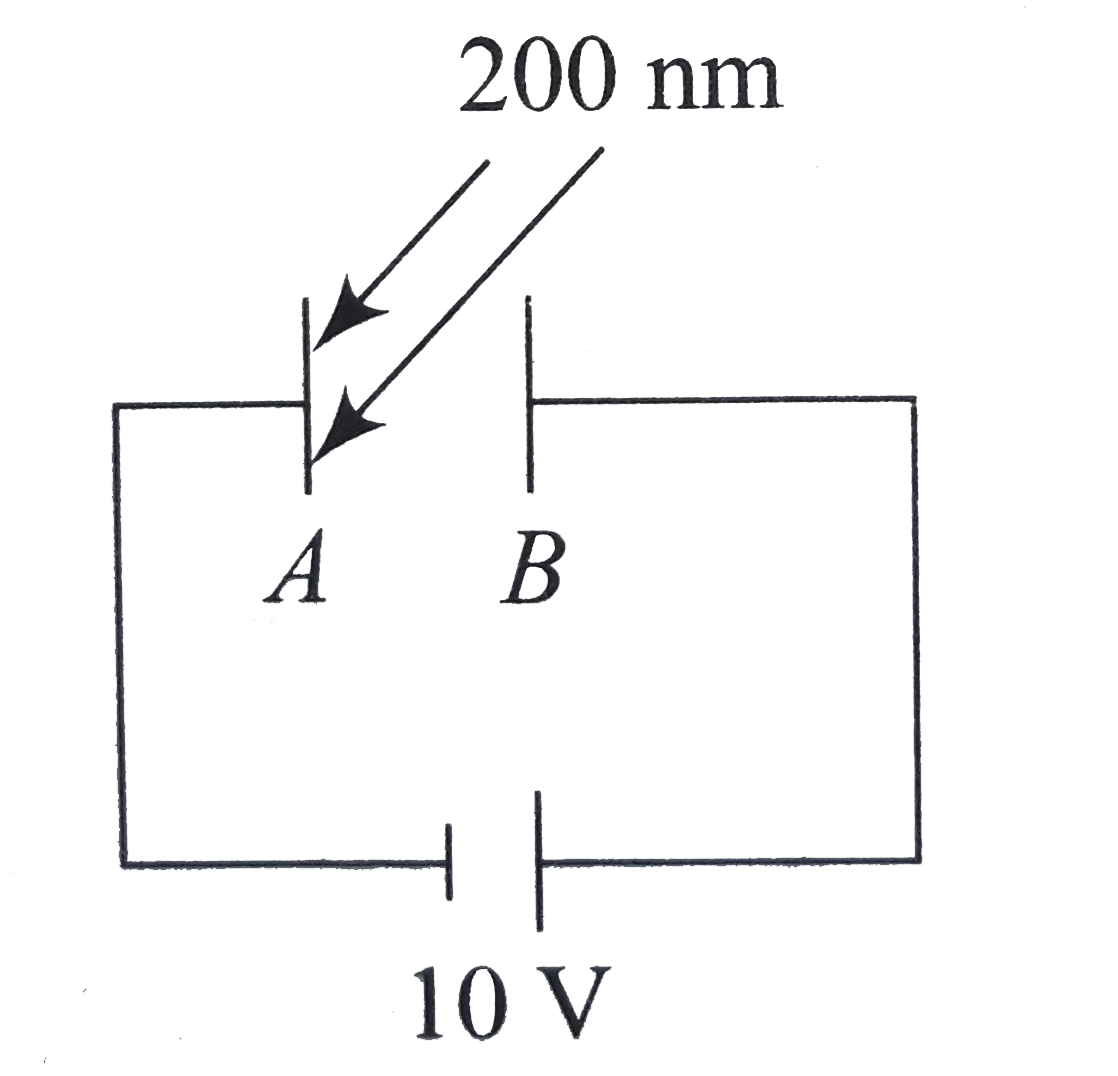
In Fig. electromagnetic radiations of wavelength 200nm are incident on a metallic plate A. the photoelectrons are accelerated by a potential difference of 10 V. These electrons strike another metal plate B from which electromagnetic radiations are emitted. The minimum wavelength of emitted photons is 100nm. If the work function of metal A is found to be (×x10−1)ev, then find the value of x. (Given hc=1240eV nm)
View SolutionAn electron is accelerated through a potential difference of V volit .Find th e de Broglie wavelength associated with electron.
View SolutionThe wavelength associated with an electron accelerated through a potential difference of 100V is nearly
View SolutionThe cut-off wavelength of an X-ray depends on
View Solution