Question

If in previous illustration, The charge particle is projected at angle ${\displaystyle \alpha }$ with x-axis with magnitude of velocity. Find
a. velocity vector in function of time ${\displaystyle \overrightarrow{v}\left(t\right).}$
b. position vector in function of time ${\displaystyle \overrightarrow{r}\left(t\right).}$

Explanation

We can make components of the velocity of the particle along x-axis and y-axis. The component which is along the magnetic field will remain unchanged. But the component perpendicular to the magnetic field will provide circular motion. In a combined way, the path of the particle will be helical.

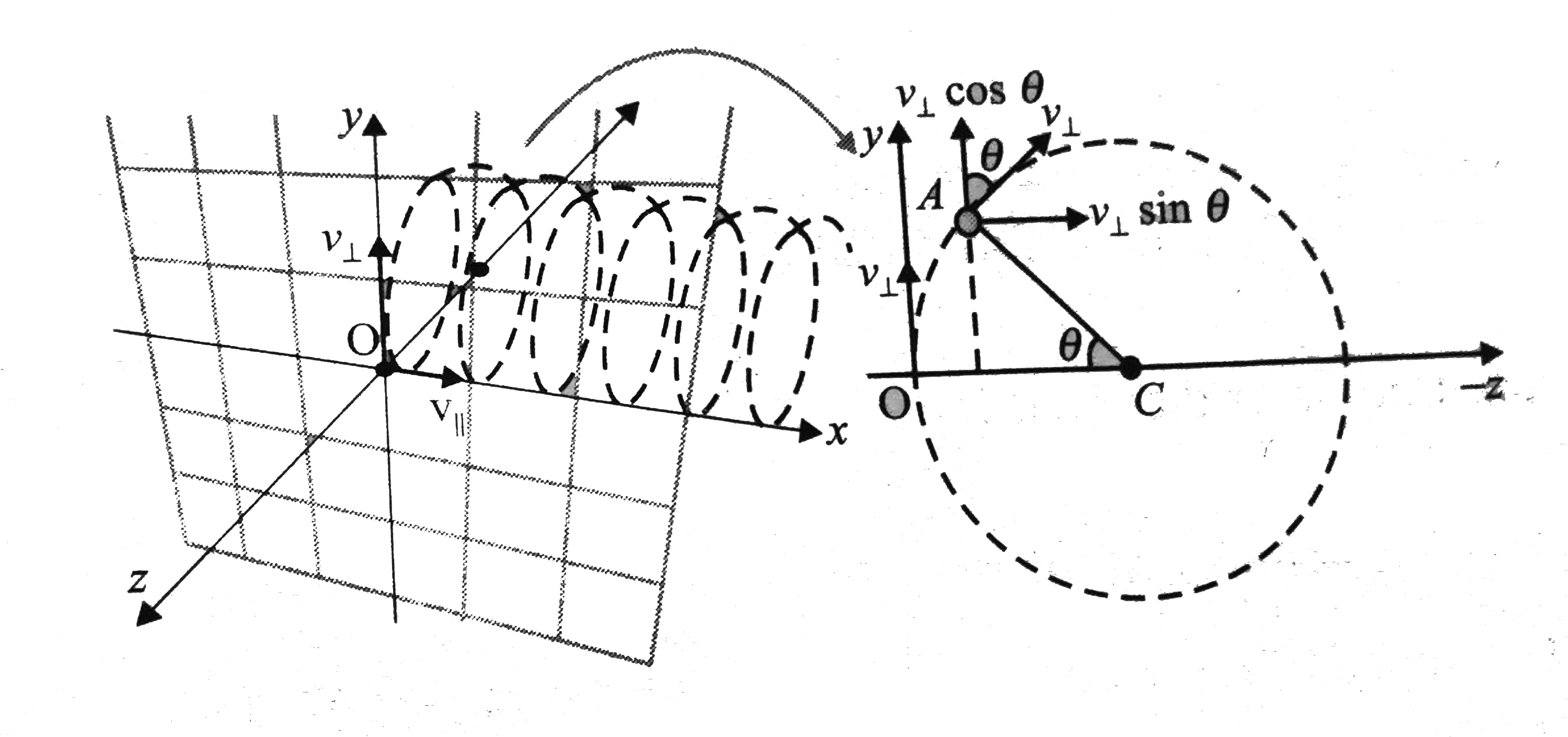
The component of velocity parallel to magnetic field
`v_(||)=v cos alpha`
The component of velocity perpendicular to magnetic field
`v_(bot)=v sin alpha`
The y and z components of velocity and position vector can be calculated in the same way as in previous illustration. The only difference is in place of v we substitute `v_(bot)`. Hence, velocity vector `[vecv_(bot)(t)]` in function of time can be writtens as
`vecv_(bot)(t)=v_(bot)cos. (qB)/m t hatj-v_(bot) sin. (qB)/m t hatk`
Hence net velocity
`vec (v) =v_(||)hat(i)+v_(bot) cos.(qB)/(m)t hat(j)-v_(bot) sin.(qB)/(m)t hat(k)`
And position vector in function of time
`vecr(t)=v_(||)t hati+R sin.(qBt)/m hatj-R(1-cos.(qBt)/m)hatk`.