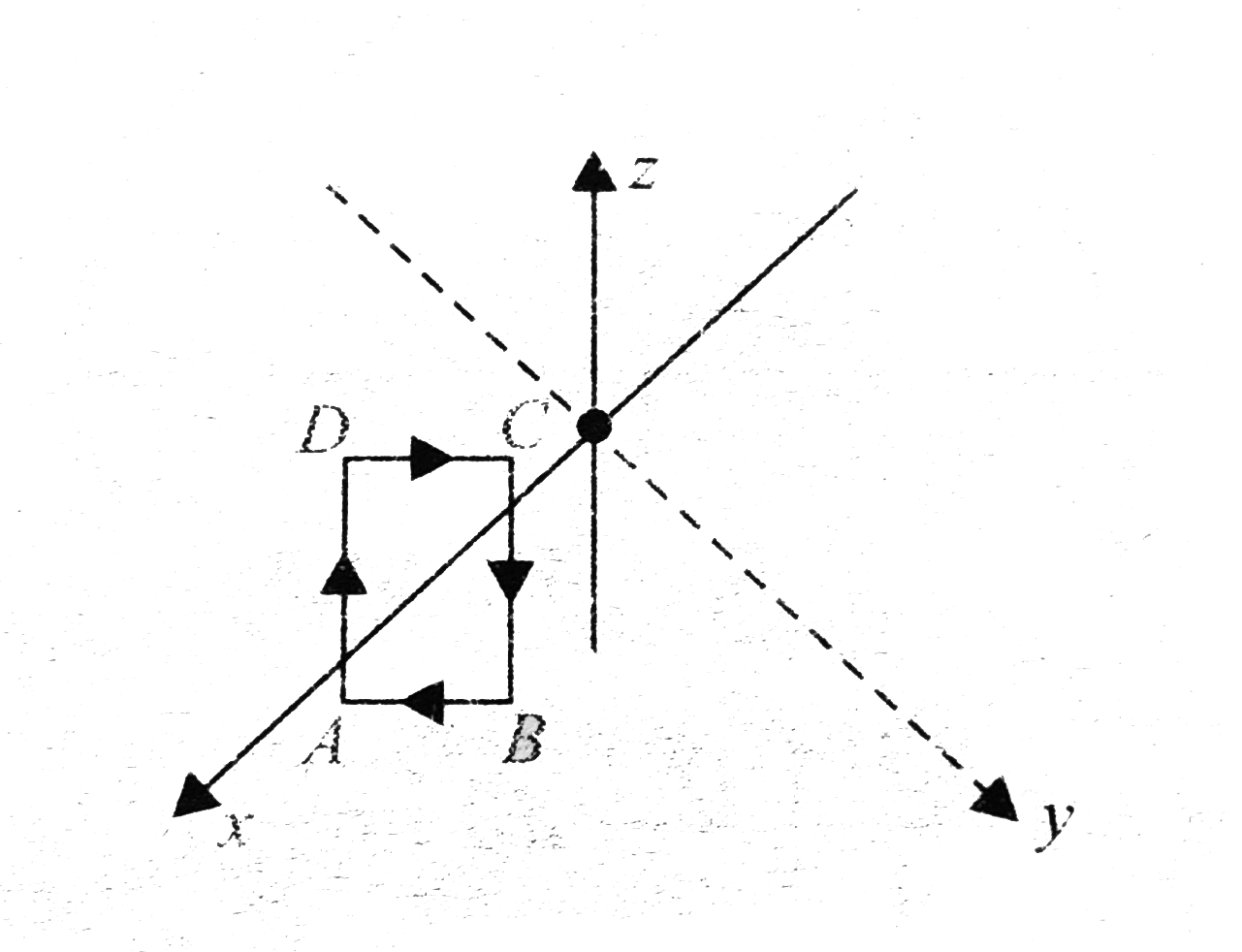A current I flows in a rectangularly shaped wire whose centre lies at and whose vertices are located at the points A respectively. Assume that a,b,d << . Find the magnitude of magnetic dipole moment vector of the rectangular wire frame in . (Given, b=10 m,I=0.01A, d=4m,a=3m).
The correct Answer is:2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Archives Fill In The Blank6videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Archives True /false4videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Linked Comprehension28videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based8videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False3videos
MISCELLANEOUS VOLUME 3
Similar Questions
If the points (a,0),(b,0),(0,c), and (0,d) are concyclic (a,b,c,d>0), then prove that ab=cd.
View SolutionIf the point (x,4) lies on a circle whose centre is at the origin and radius is 5, then x= ±5 (b) ±3 (c) 0 (d) 14
View SolutionIf c,d are the roots of the equation (x−a)(x−b)−k=0 , prove that a, b are roots of the equation (x−c)(x−d)+k=0.
View SolutionIf a≠0andlogx(a2+1)<0 then x lies in the interval
(A) (0,∞)
(B) (0,1)
(C) (0,a)
(D) none of theseView SolutionLet a and b are the roots of the equation x2−10xc−11d=0 and those of x2−10ax−11b=0,. are c and d then find the value of a+b+c+d
View SolutionIfa,b,c,d∈R such that a<b<c<d, then roots of the equation (x−a)(x−c)+2(x−b)(x−d)=0
View SolutionThe function xx decreases in the interval (a) (0,e) (b) (0,1) (c) (0,1e) (d) none of these
View SolutionIf 1 is the twice repeated root of the equation ax3+bx2+bx+d=0,then (a) a=b=d (b) a+b=0 (c) b+d=0 (d) a=d
View SolutionEvaluate the following limit: (lim)x→0ax+bcx+d, d≠0
View SolutionA circle with center (a,b) passes through the origin. The equation of the tangent to the circle at the origin is (a)ax−by=0 (b) ax+by=0 bx−ay=0 (d) bx+ay=0
View Solution