A coil of radius R carries current i1. Another concentric coil of radius r(r<<R) carries current i2. Planes of two coils are mutually perpendicular and both the coil are free to rotate about common diametre. Find maximum kinetic energy of smaller coil when both the coils are released, masses of coils are M and m, respectively.
Magnetic induction at centre due to current in
larger coil is
B=μ0i12R
Magnetic dipole moment of smaller coil
M=πr2i2
Initially M and B are at 90∘
So, U1=−MBcos90∘=0
when the coils become coplanar
U2=−MBcos0∘=−MB
Decrease in potential energy =U1−U2=MB=μ0i1i2πr22R
This decrease in potential energy convert into kinetic energy.
Here the kinetic energies are maximum when the coils become
coplanar. The two coils rotate due to their mutual interaction
only and if one coil rotates clockwise, then the other coil rotates
anticlockwise.
Let ω1andω2 be the angular velocities of larger and smaller coils
when they become coplanar. According to law of conservation of angular momentum,
I1ω1=I2ω2
and according to law of conservation of energy
12I1ω21+12I2ω22=U
From above two equations, we get
12I1(I2ω2I1)2+12I2ω22=U⇒12I1ω22(I1I2+1))=U
⇒12I1ω22=UI1I1+I2
So maximum kinetic energy of smaller coil is given by
⇒12I1ω22=(μ0i1i2πr22R)((1/2)MR2(1/2)MR2+(1/2)mr2)
μ0i1i2πr2MR2(MR2+mr2)
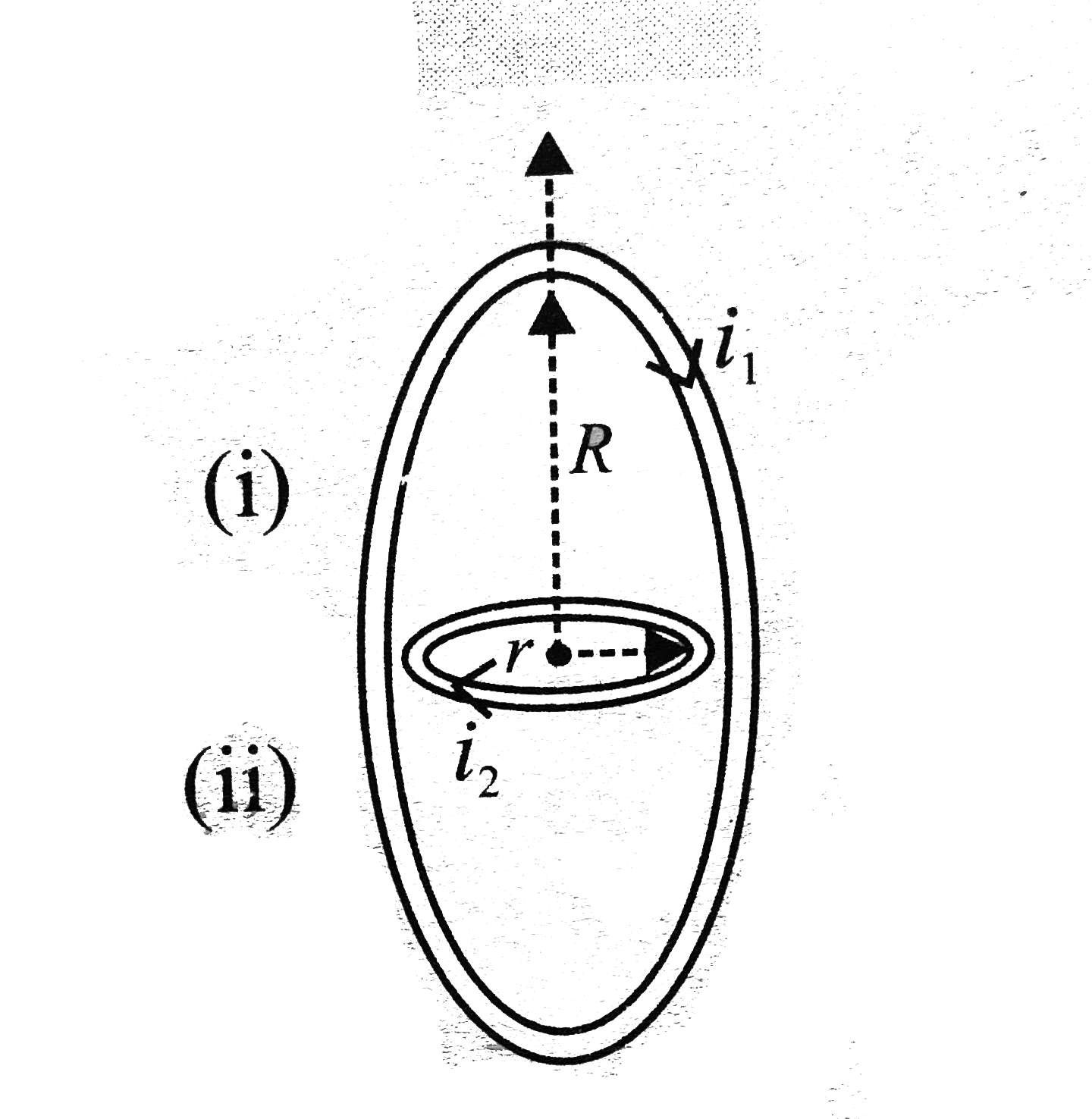
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.135videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.210videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type12videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.612videos
RAY OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type14videos
WAVE OPTICS
Similar Questions
A coil of radius R carries a current i1. Another concentric coil of radius r(r<<R) carries a current i2. Planes of two coils are mutually perpendicular and both the coils are free to rotate about common diameter. Find maximum kinetic energy attained by the two coils, when both are released from rest. The masses of two coils are M and m respectively.
Strategy : The magnetic field due to coil of radius R is μ0i12R. This field exerts a torque on shorter coil. An equal and opposite torque is exerted by the shorter coil on larger coil. There is no external torque acting on the system. The angular momentum remains conserved. Also the total mechanical energy remains conserved. At any instant, let ω1andω2 represent the angular velocityView SolutionA circular coil of n turns and radius r carries a current I. The magnetic field at the centre is
View Solution
Knowledge Check
- Question 1 - Select One
A 200 turn closely wound circular coil of radius 15 cm carries a current of 4 A. The magnetic moment of this coil is
A36.5Am2B56.5Am2C66.5Am2D108Am2 - Question 2 - Select One
A circular coil of radius 10 cm having 100 turns carries a current of 3.2 A. The magnetic field at the center of the coil is
A2.01×10−3TB5.64×10−3TC2.64×10−3TD5.64×10−3T
Find the mutual inductance of two concentric coils of radii a1 and a2(a1<<a2) if the planes of the coils are perpendicular.
View SolutionA small coil of radius r is placed at the centre of a large coil of radius R, where R>>r. The two coils are coplanar. The mutual inductance between the coils is proportional to
View SolutionA coil of radius r is placed at the centre of the large coil of radius R where R⟩r and coils are in same plane.The coefficient of mutual inductance between the coil is
View SolutionA circular coil of radius 2R is carrying current 'i' . The ratio of magnetic fields at the centre of the coil and at a point at a distance 6R from the centre of the coil on the axis of the coil is
View SolutionA circular coil of radius 1⋅5cmcarriesacurrentof1⋅5A. If the coil has 25 turns , find the magnetic field at the centre.
View SolutionA 100 turn closely wound circular coil of radius 10cm carries a current of 3⋅2A.What is the field at the centre of the coil?
View Solution
