Two identical cycle wheels (geometrically have different number of spokes connected from center to rim. One if having 20 spokes and the other having only 10 (the rim and the spokes are resistance less). One resistance of value R is connected between centre and rim. The current in R will be
(a) double in the first wheel than in the second wheel
(b) four times in the first wheel than in the second wheel
( C) will be double in the second wheel than that of the first wheel
(d) will be equal in both these wheels
The correct Answer is:D
To solve the problem, we need to analyze the situation involving two identical cycle wheels with different numbers of spokes, and how the induced electromotive force (emf) affects the current through a resistance R connected between the center and the rim.
1. Understanding the Setup:
- We have two identical cycle wheels, one with 20 spokes and the other with 10 spokes.
- Both wheels are rotated in a uniform magnetic field with the same angular speed ω.
- A resistance R is connected between the center and the rim of each wheel.
2. Induced EMF Calculation:
- The induced emf E in a rotating wheel can be calculated using the formula:
E=12Bωr
where B is the magnetic field strength, ω is the angular speed, and r is the radius of the wheel.
3. Distribution of EMF Across Spokes:
- Each spoke acts like a conductor that contributes to the total induced emf.
- Since the spokes are resistance-less, the induced emf across each spoke will be the same.
- For both wheels, the total induced emf across the rim will be the same since they are geometrically identical and rotating in the same conditions.
4. Equivalent EMF in Parallel Configuration:
- The spokes in each wheel can be considered as being in parallel.
- For parallel configurations of identical cells (or spokes), the equivalent emf remains the same as that of a single spoke.
- Therefore, the total emf across the rim for both wheels is E.
5. Current Calculation:
- The current I flowing through the resistance R connected between the center and the rim can be calculated using Ohm's law:
I=ER
- Since the induced emf E is the same for both wheels, the current I will also be the same.
6. Conclusion:
- The current in the resistance R connected to both wheels will be equal.
- Therefore, the answer to the question is that the current in R will be the same for both the wheels.
Final Answer:
The current in resistance R will be equal in both cases.
- We have two identical cycle wheels, one with 20 spokes and the other with 10 spokes.
- Both wheels are rotated in a uniform magnetic field with the same angular speed ω.
- A resistance R is connected between the center and the rim of each wheel.
- The induced emf E in a rotating wheel can be calculated using the formula:
E=12Bωr
where B is the magnetic field strength, ω is the angular speed, and r is the radius of the wheel.
- Each spoke acts like a conductor that contributes to the total induced emf.
- Since the spokes are resistance-less, the induced emf across each spoke will be the same.
- For both wheels, the total induced emf across the rim will be the same since they are geometrically identical and rotating in the same conditions.
- The spokes in each wheel can be considered as being in parallel.
- For parallel configurations of identical cells (or spokes), the equivalent emf remains the same as that of a single spoke.
- Therefore, the total emf across the rim for both wheels is E.
- The current I flowing through the resistance R connected between the center and the rim can be calculated using Ohm's law:
I=ER
- Since the induced emf E is the same for both wheels, the current I will also be the same.
- The current in the resistance R connected to both wheels will be equal.
- Therefore, the answer to the question is that the current in R will be the same for both the wheels.
The current in resistance R will be equal in both cases.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Multiple Correct23videos
ELECTROMAGNETIC INDUCTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Asserton - Reasoning8videos
ELECTROMAGNETIC INDUCTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Subjective13videos
ELECTROMAGNETIC INDUCTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q2videos
ELECTRICAL MEASURING INSTRUMENTS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
Similar Questions
A coil having an inductance of 1/π henry is connected in series with a resistance of 300Ω. If 20 volt from a 200 cycle source are impressed across the combination, the value of the phase angle between the voltage and the current is :
View SolutionTwo identical cells each of emf ε, having negligible internal reistance r, are connercted in parallel with each other across an external resistance R. What is the current through this resistance.
View Solution
Knowledge Check
- Question 1 - Select One
A cell having an emf E and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
A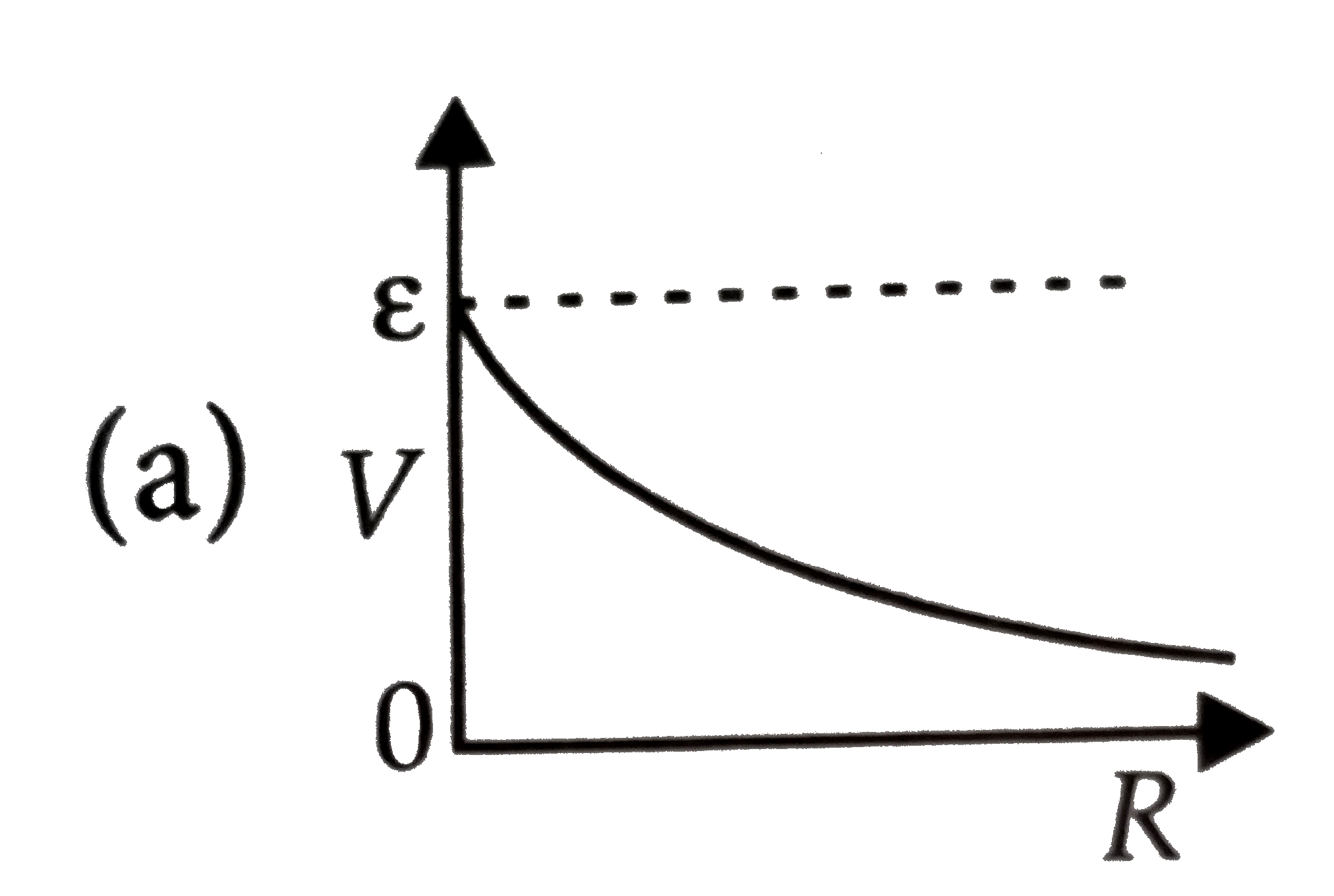 B
B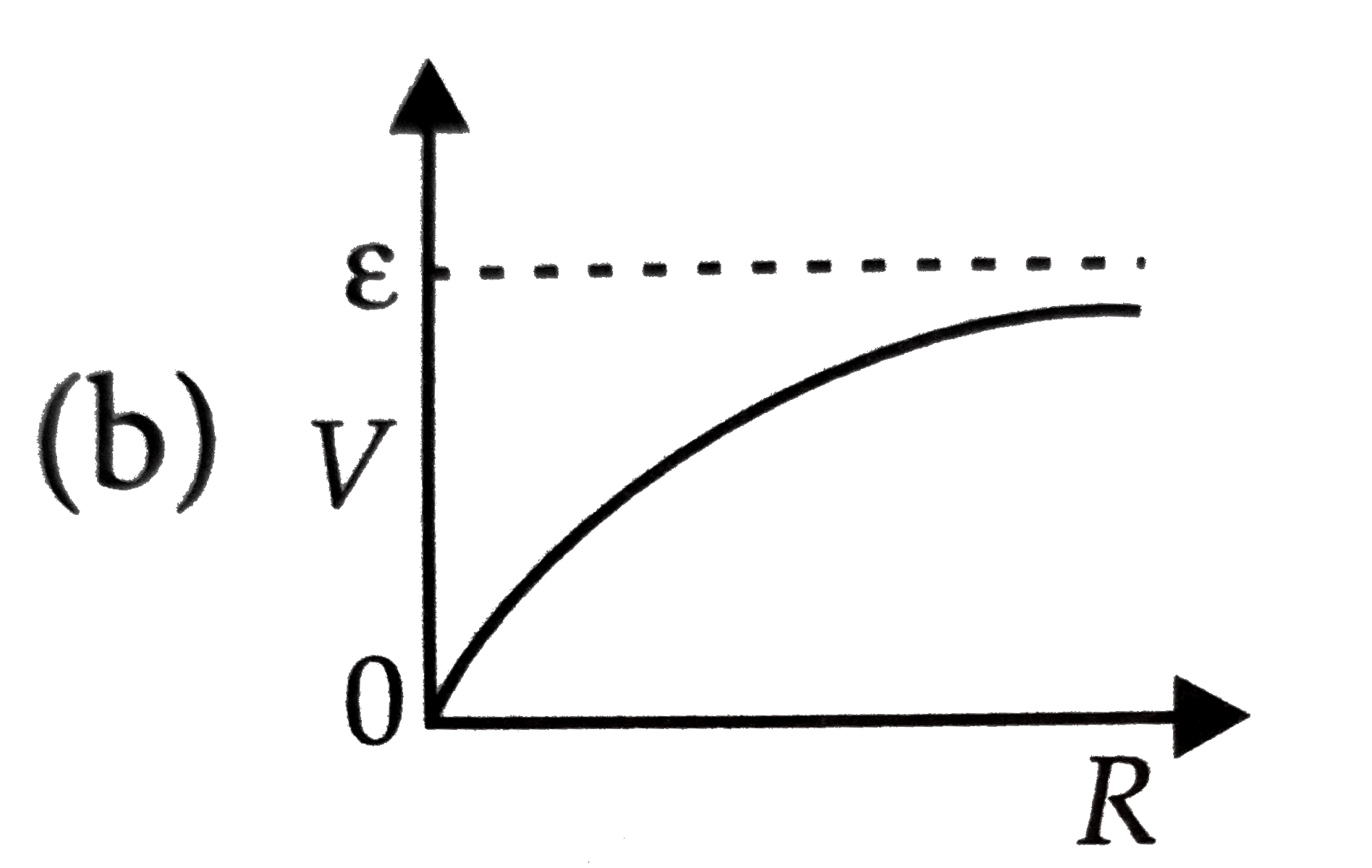 C
C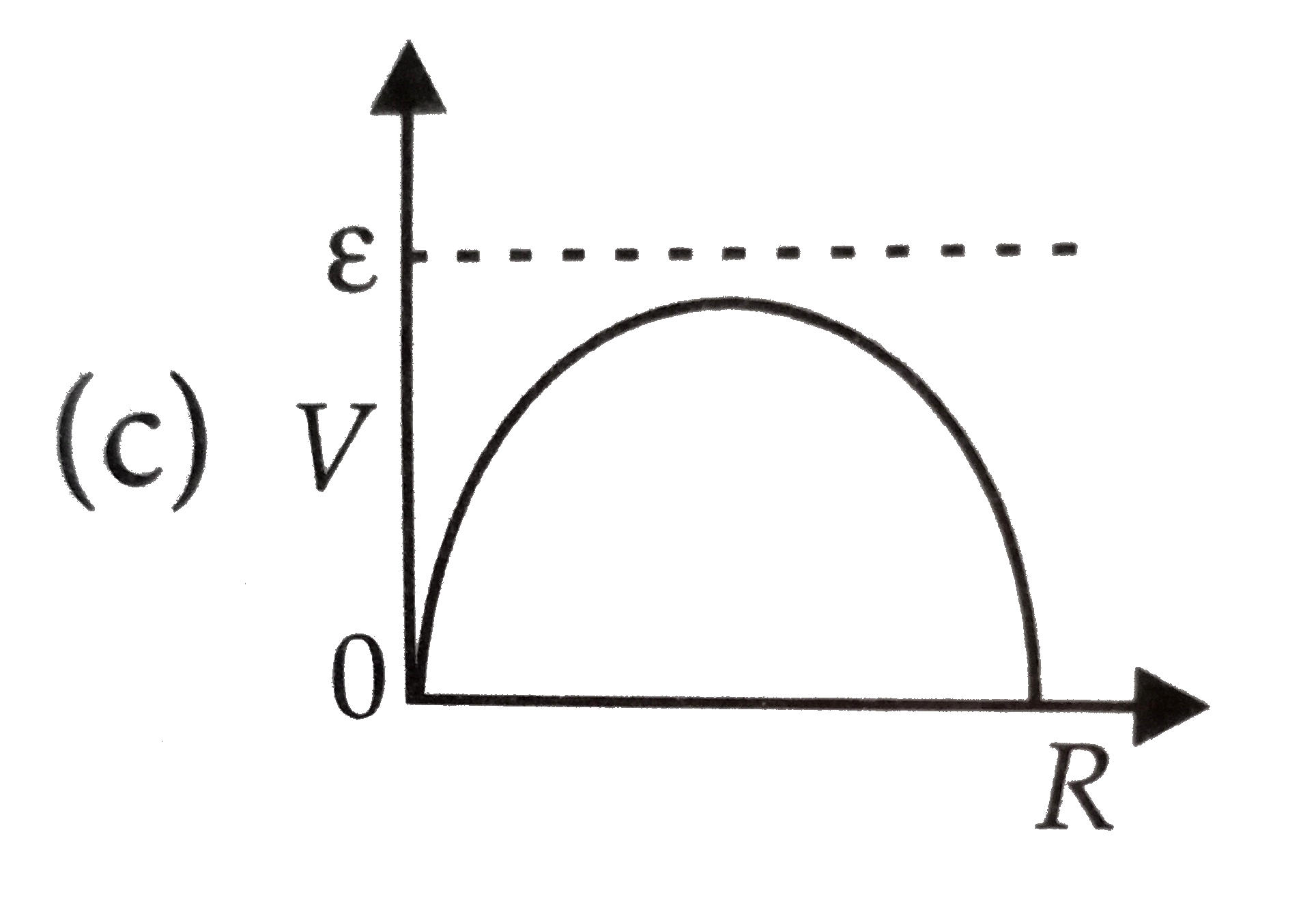 D
D
Figure shows a circuit model for the transmission of an electrical signal, such as cable TV, to a large number of subscribers. Each subscriber connects a load resistance RL between the transmission line and the ground. Assume the ground to be at zero potential and to have negligible resistance. The resistance of the transmission line between the connection points of different subscribers is modeled as the constant resistance RT. The equivalent resistance across the signal source is
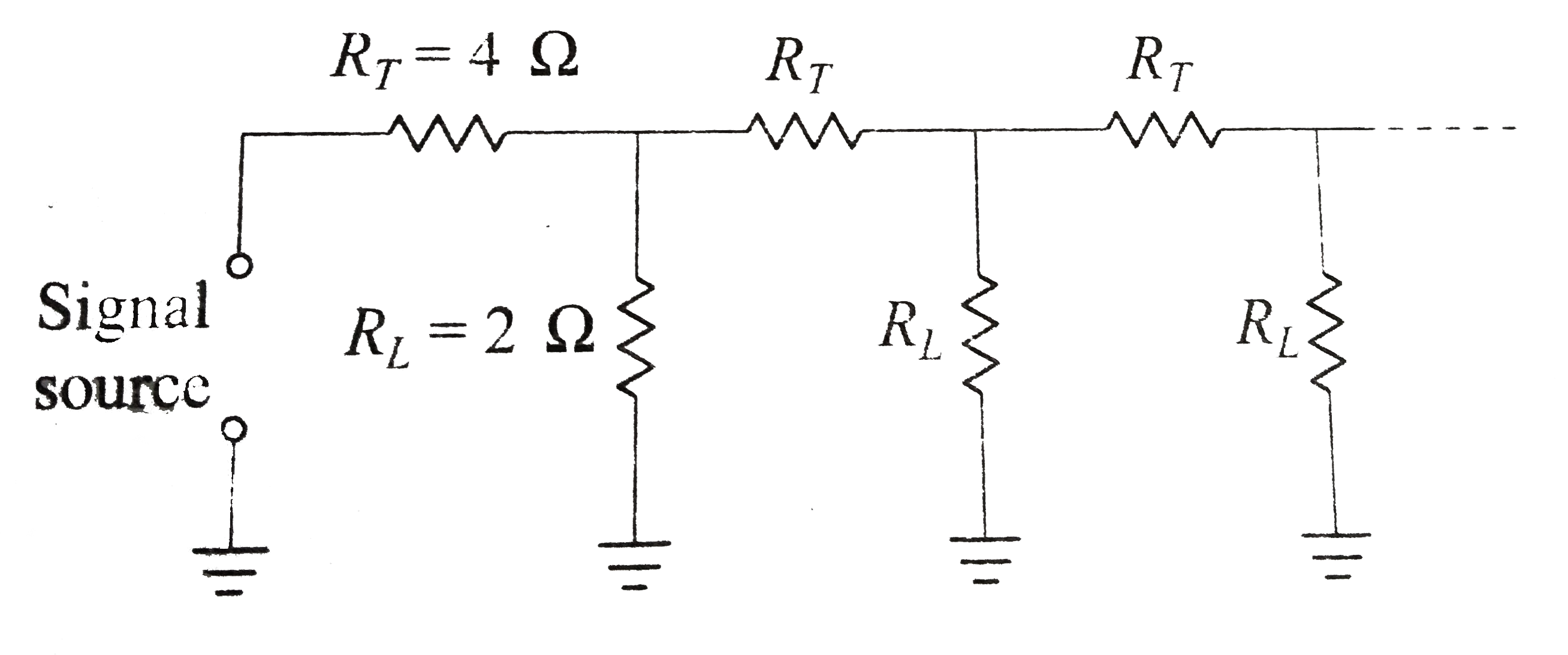 View Solution
View SolutionFour identical resistances each having value R are arranged as shown in Figure. Find the equivalent resistance between A and B.
 View Solution
View SolutionUnder what condition will the current in a wire be the same when connected in series and in parallel on n identical cells each having internal resistance r and external resistance R?
View Solutionn equal cell having emf E and internal resistance r, are connected in circuit of a resistance R. Same current flows in circuit either they connected in series or parallel, if:
View SolutionA rod of length l and resistance r rotates about one end as shown in figure.Its othr end touches a conducting ring a of negligible resistance.A resistance R is connected between centre and periphery.Draw the electrical equivalence and find the current in the resistance R.There is a uniform magnetic field B directed as shown.
 View Solution
View SolutionIn the given diagram, there are two semicircular parts one having radius 'a' and another having radius '3a' as shown. If resistance of ACB part is R and resistance of ADB part is 3R. Select the correct option(s):
 View Solution
View SolutionThe spokes of a wheel are made of metal and their lengths are of one metre. On rotating the wheel about its own axis in a uniform magnetic field of 5×10−5 tesla normal to the plane of the wheel, a potential difference of 3.14mV is generated between the rim and the axis. The rotational velocity of the wheel is-
View Solution

