A metal bar AB can slide on two parallel thick metallic rails separated by a distance l. A resistance R and an inductance L are connected to the rails as shown in the figure. A long straight wire carrying a constant current is placed in the plane of the rails and perpendicular to them as shown. The bar AB is held at rest at a distance from the long wire. At t=0, it is made to slide on the rails away from wire. Answer the following questions.
(a) Find a relation among , where i is the current in the circuit and is the flux of the megnetic field due to the long wire through the circuit.
(b) It is observed that at time t=T, the metal bar AB si at a distance of from the long wire and the resistance R carries a current . Obtain an expression for the net charge that has flown through riesistance R form t=0 to t=T.
(c) THe bar is suddenly stopped at time T. THe current through resistance R is found to be at time 2T. Find the value of in terms of hte other given quantities.
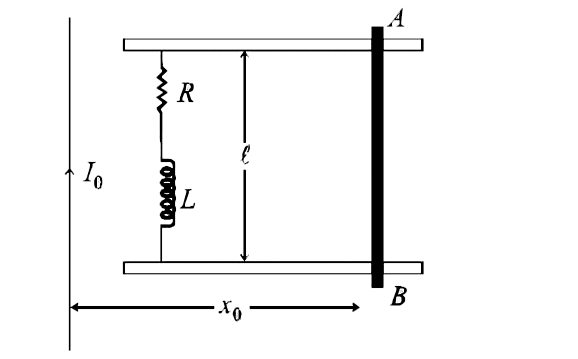
a. When bar slider away, the magneic force acts on free electrons along negative Y-axis, so electrons move from end to end , making end at positive potential relative to end . So current in the circuit will flow from to as shows.
Let be the induced emf According to kirchhoff's second law,
But (numerically)
(i)
This i sthe required relation.
b. Equation (i) can be expressed as
Integrating, we get
Charge flows from to will be
(ii)
Change in flux during the displacement of bar from to in time is
(iii)
From Eq.(ii), charge flows
(iv)
c. The equation of decay of current in an circuit is given by
(v)
Given
Substituting these values in Eq.(v), we get
or

Topper's Solved these Questions
- INDUCTANCEBook:CENGAGE PHYSICS ENGLISHChapter:INDUCTANCEExercise:Exercise 4.1
Explore 24 Videos
- INDUCTANCEBook:CENGAGE PHYSICS ENGLISHChapter:INDUCTANCEExercise:Exercises (subjective)
Explore 7 Videos
- INDUCTANCEBook:CENGAGE PHYSICS ENGLISHChapter:INDUCTANCEExercise:Concept Based
Explore 8 Videos
- HEATING EFFECT OF CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:HEATING EFFECT OF CURRENTExercise:Thermal Power in Resistance Connected in Circuit
Explore 27 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBook:CENGAGE PHYSICS ENGLISHChapter:MAGNETIC FIELD AND MAGNETIC FORCESExercise:Multiple Correct Answer type
Explore 2 Videos
Similar Questions
In the figure shown a current I1 is established in the long straight wire AB. Another wire CD carrying currrent I2 is placed in the plane of the paper. The line joining the ends of this wire is perpendicular to the wire AB. The resultant force on the wire CD is :
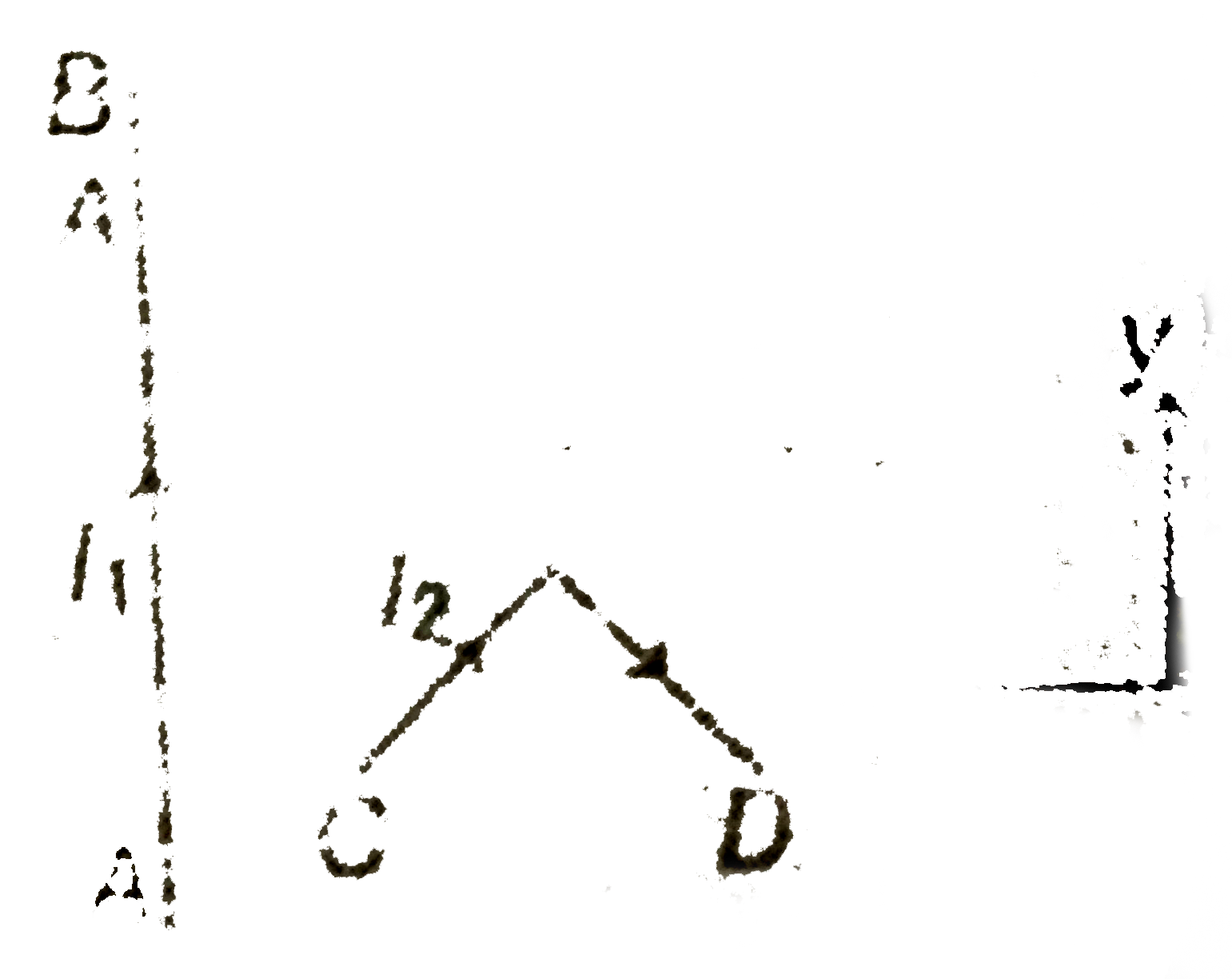
View SolutionA metallic rod of mass m and resistance R is sliding over the 2 conducting frictionless rails as shown in Fig. An infinitely long wire carries a current I0. The distance of the rails from the wire are b and a respectively.
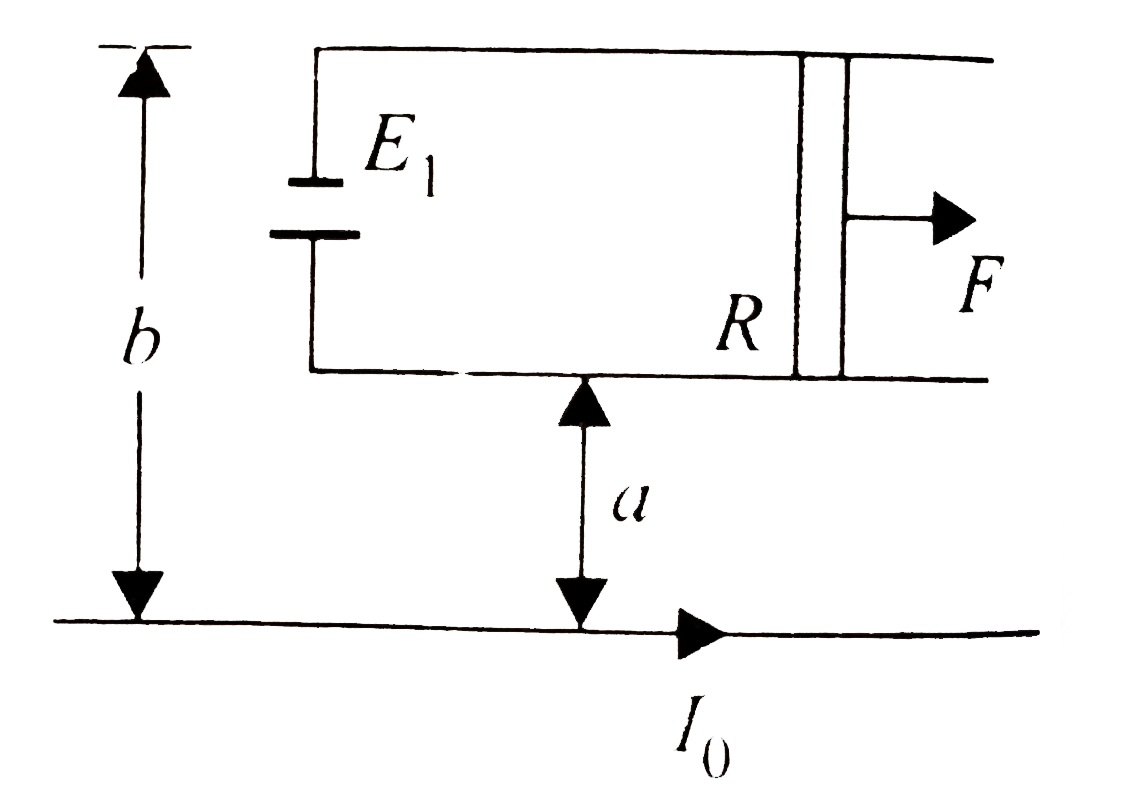
Find the value of F if the rod slides with constant velocity
View SolutionA rod of length l is kept parallel to a long wire carrying constant current i . It is moving away from the wire with a velocity v. Find the emf induced in the wire when its distance from the long wire is x.
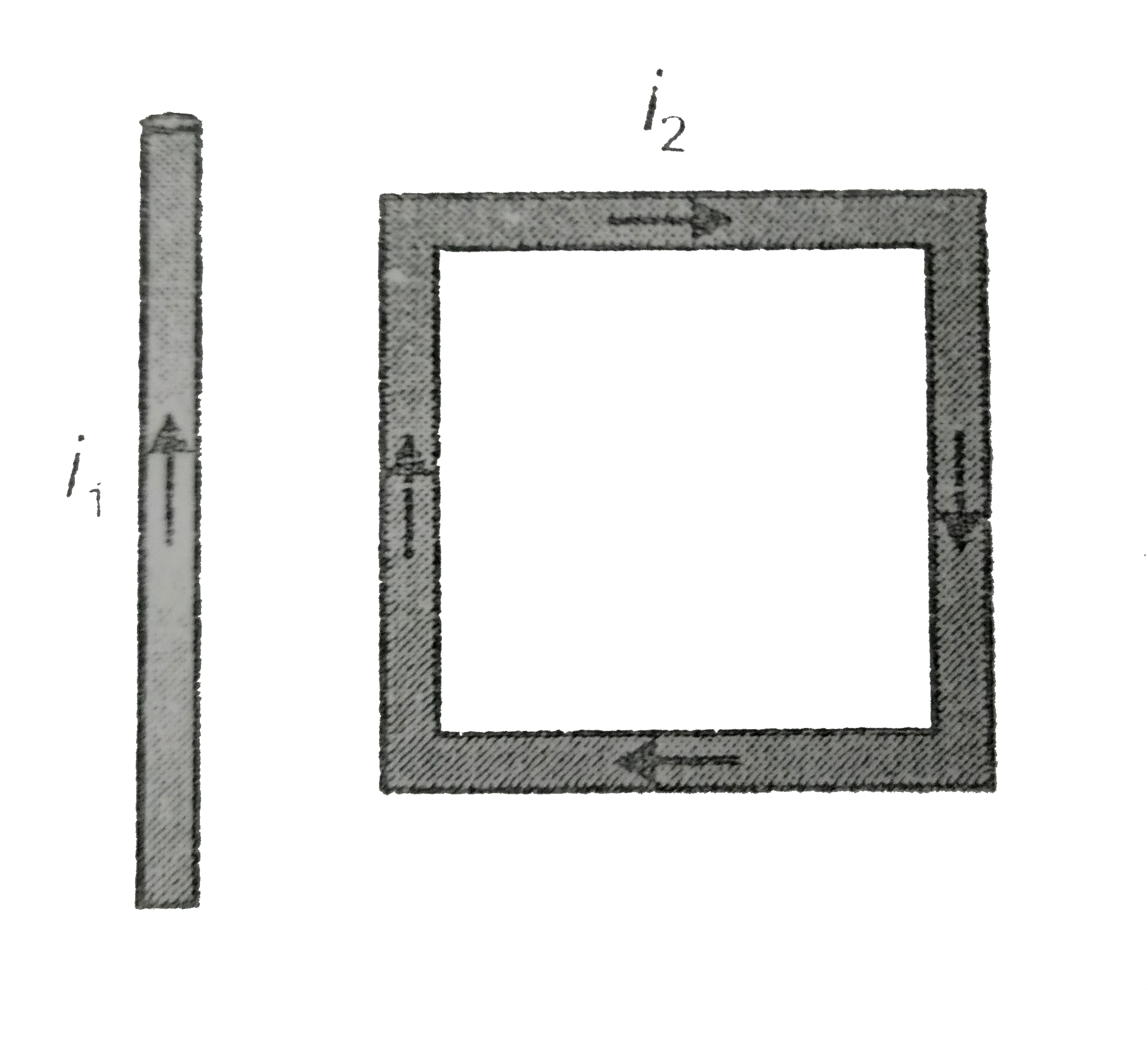
View SolutionA rectangular loop carrying a current i2 situated near a long straight wire carrying a steady current i1. The wire is parallel to one of the sides of the loop and is in the plane of the loop as shown in the figure. Then the current loop will
View SolutionA metallic rod of mass m and resistance R is sliding over the 2 conducting frictionless rails as shown in Fig. An infinitely long wire carries a current I0. The distance of the rails from the wire are b and a respectively.
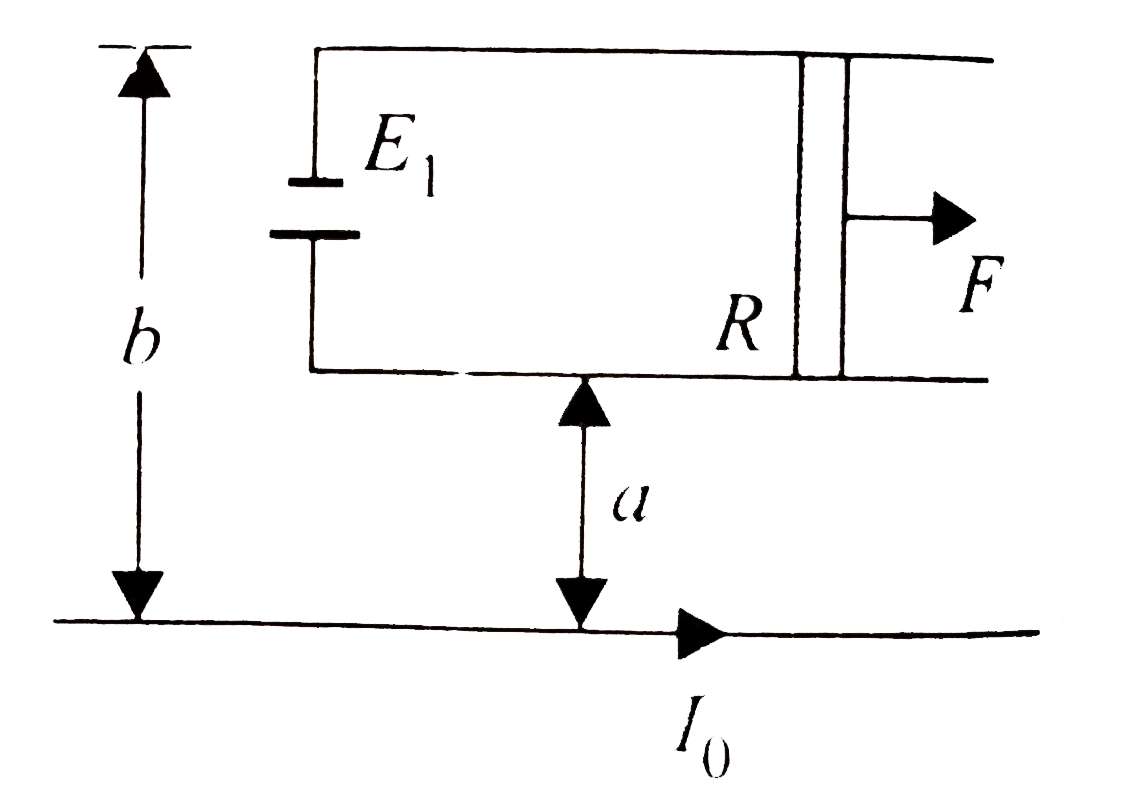
Find the value of current in the circuit if the rod slides with constant velocity v0
View SolutionA conductor AB of length l carrying current i is placed perpendicular to a long straight conductor carrying a current I as shown. Force on AB will be

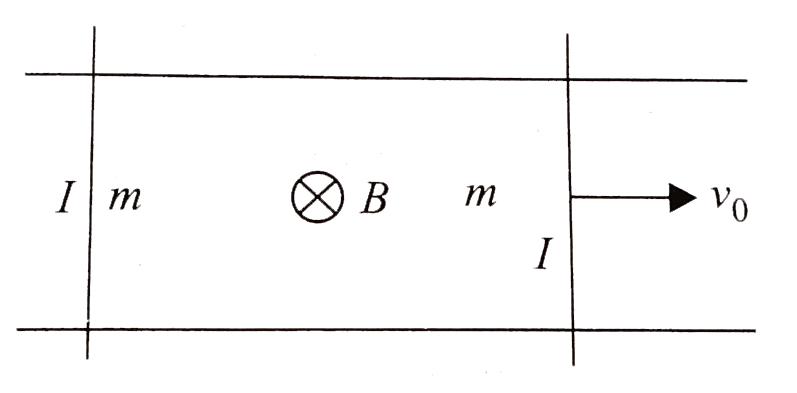
View SolutionConsider parallel conducting rails separated by a distance l. There exists a uniform magnetic field B perpendicular to the plane of the rails as shown in Fig. Two conducting wires each of length l are placed so as to slide on parallel conducting rails. One of the wires is given a velocity v0 parallel to the rails. Till steady state is achieved, loss in kinetic energy of the system is
View SolutionTwo parallel infinite wires separated by distance d carry currents as shown in figure,
_2019_CBT5_E01_052_Q01.png)
The distance from a third infinite wire be kept parallel to wire carrying current I1, the wire such that it stays in equilibrium is
View SolutionA conductor AB of length L carrying a current I', is placed perpendicular to a long straight conductor XY carrying a current I as shown in Fig. The forces on AB has magnitude

View SolutionA conductor AB of length L carrying a current I', is placed perpendicular to a long straight conductor XY carrying a current I as shown in Fig. The forces on AB has magnitude

View Solution
