In the given circuit, initially switch S1 is closed, and S2 and S3 are open. After charging of capacitor, at t=0, S1 is opened and S2 and S3 are closed. If the relation between inductance, capacitance and resistance is L=4CR2, tehn find the time (in s) after which current passing through capacitor and inductor will be same (given R=In2mΩ,L=2mH)

The correct Answer is:(1)
After charging, charge on capacitor =Cε
Now, at t=0 two circuits are formed
1. Discharging of capacitor
q=Cεe−t/τC=Cεe−t/RC
i1=−dqdt=ε2Re−t/RC
2. Growth of current in L−R circuit.
i2=ε2R[1−e−t/τL]
Now, i1=i2
(ε).2Re−t/τC=ε2R[1−e−t/τL] ..(i)
Given l=4CR2
L2R=2RC=1In2⇒τC=τL=1In2
Solve to get t=1s
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Archives (fills In The Blanks)
3 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Archives (single Correct )
8 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (linked Compreshension)
36 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
Similar Questions
In given circuit initially switch Sw1 is closed and Sw2 is open, Now Sw1 is opened and Sw2 is closed, what is the heat liberated in resistance R?

View SolutionIn the circuit shown if Fig. the switch S is closed at time t = 0. The current through the capacitor and inductor will be equal at time t equal (given R=√L/C
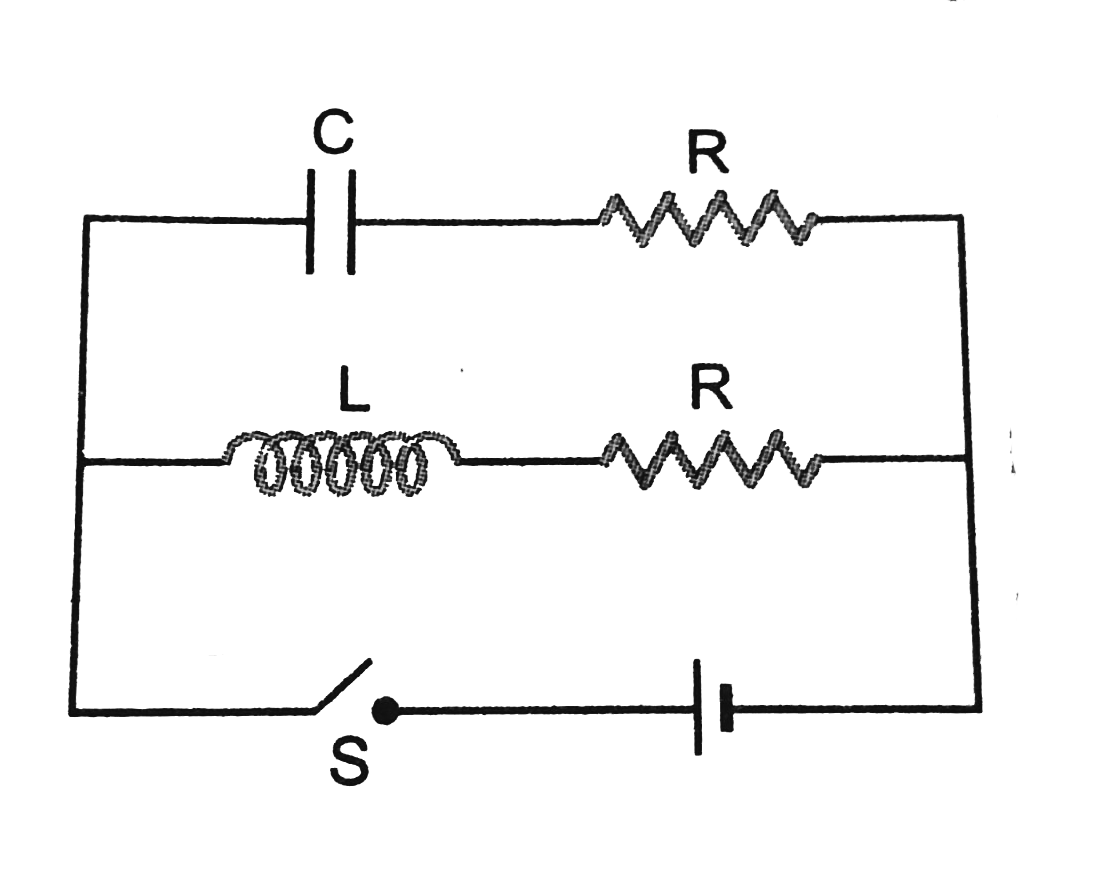
View SolutionIn the circuit shown in the figure, if switches S1 and S2 have been closed for a long time, then charge on the capacitor.
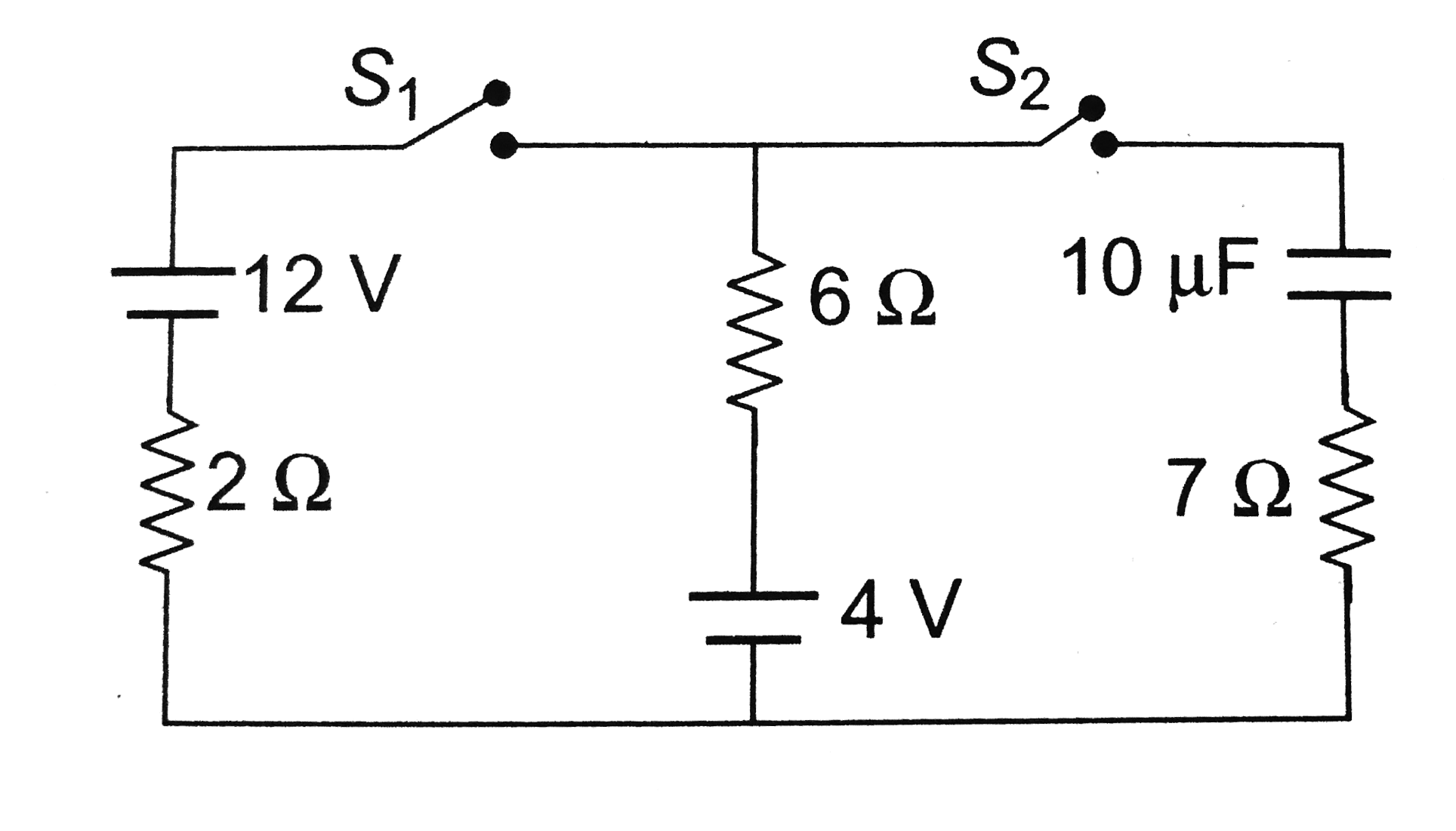
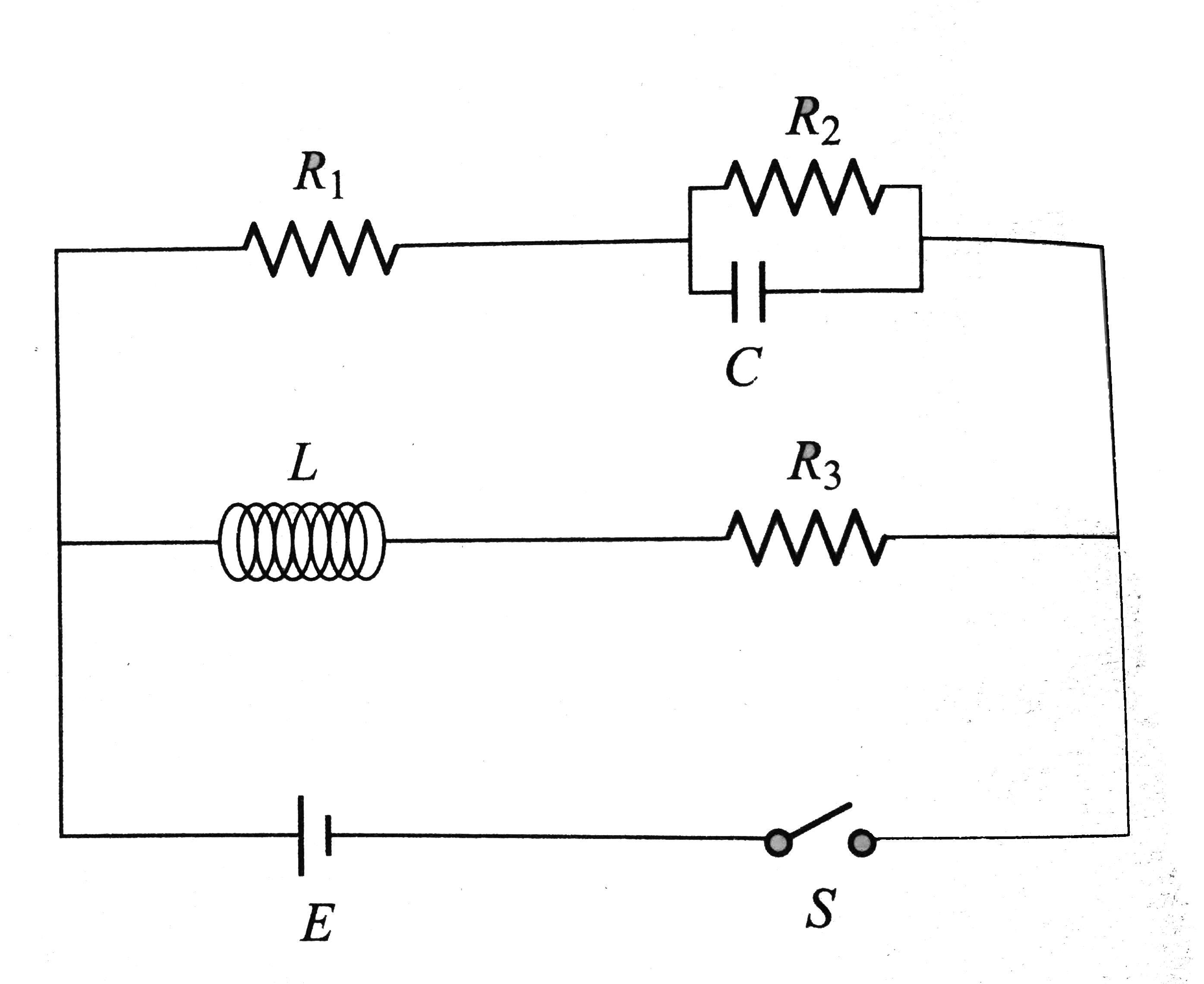
View SolutionSwitch S is cloesd in the circuit at time t=0. Find the current through the capacitor and the inductor at any time t
View SolutionIn the circuit shows (Fig.) switches S1 and S3 have been closed for 1s and S2 remained open. Just after 1s, switch S2 is closed and S1 and S3 are opened. Find after that instant (t=0):
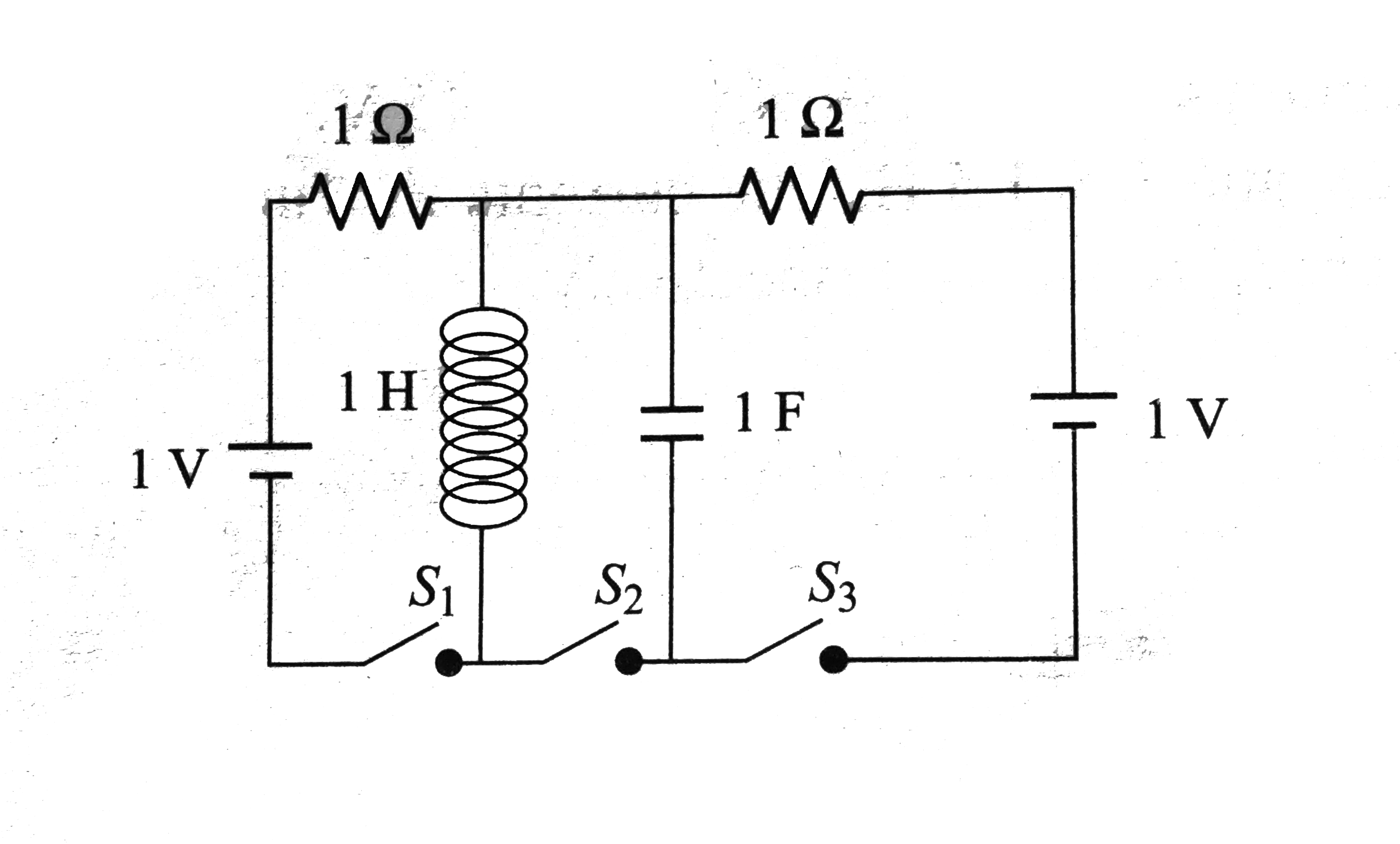
the maximum charge on the capacitor
View SolutionIn the circult shown
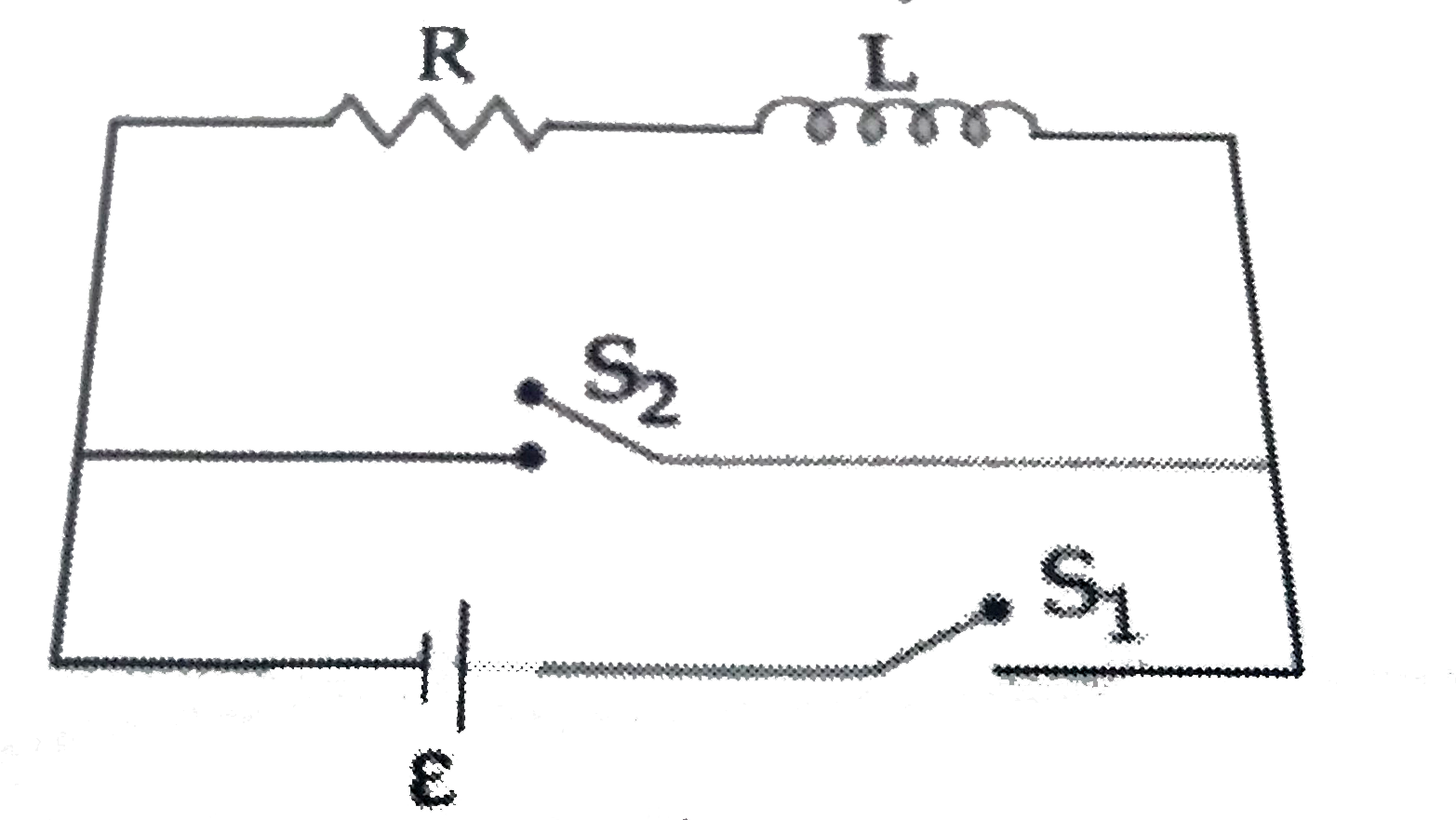 the switch S1 is closed at time t=0 and the swith S2 is kept open. At some later time (t0) ,the swith S1 is opened and S2 is closed .The behaviour of the current I as a function of time 't' is given by :
the switch S1 is closed at time t=0 and the swith S2 is kept open. At some later time (t0) ,the swith S1 is opened and S2 is closed .The behaviour of the current I as a function of time 't' is given by :
View SolutionIn given circuit all capacitor were uncharged initially. First switch S1 is closed for long time. When circuit reaches to steady state S1 is opened and S2 closed.

The current through R2 jus after closing the switch S2 is
View SolutionIn the given circuit switch S2 is Kept closed and S1 is kept open for a very long time such that the system is in steady- state . Now S1 is also slosed keeping S2 closed.
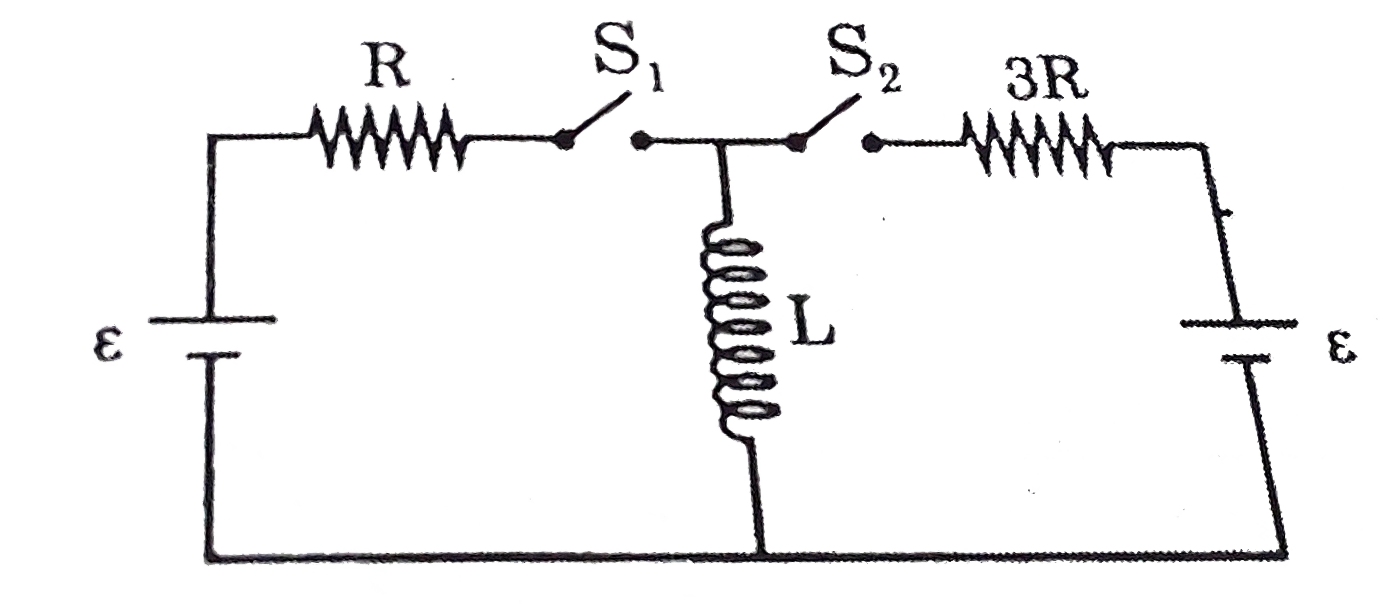
Current passing through inductor L time after S1 is closed , is :
View SolutionConsider the network shown in initially, the switch S1 is closed and S2 is open.
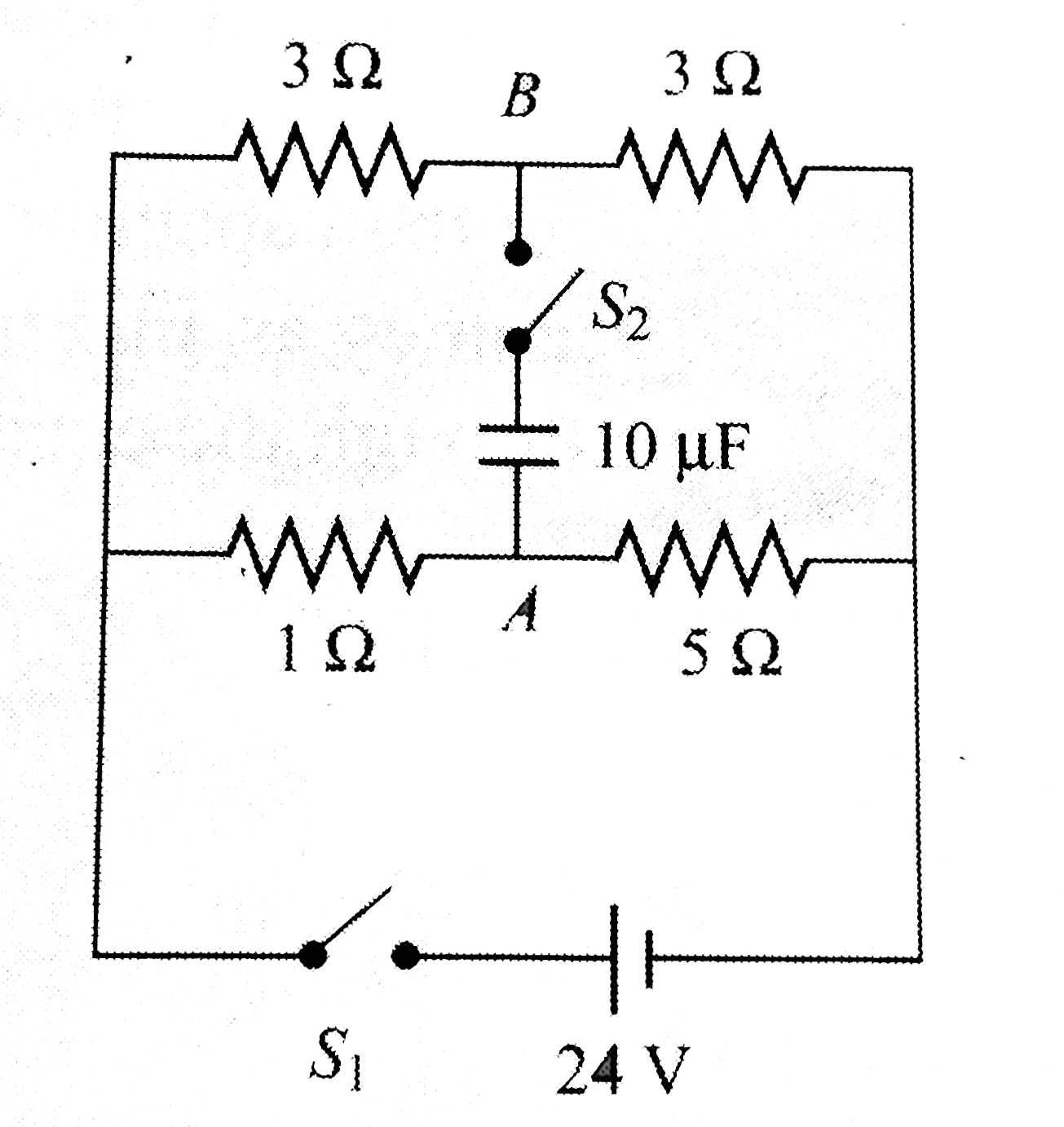
a. Calculate VA−VB.
b. When S2 is also closed, what is VA−VB
i. just after closing , ii. After long time.
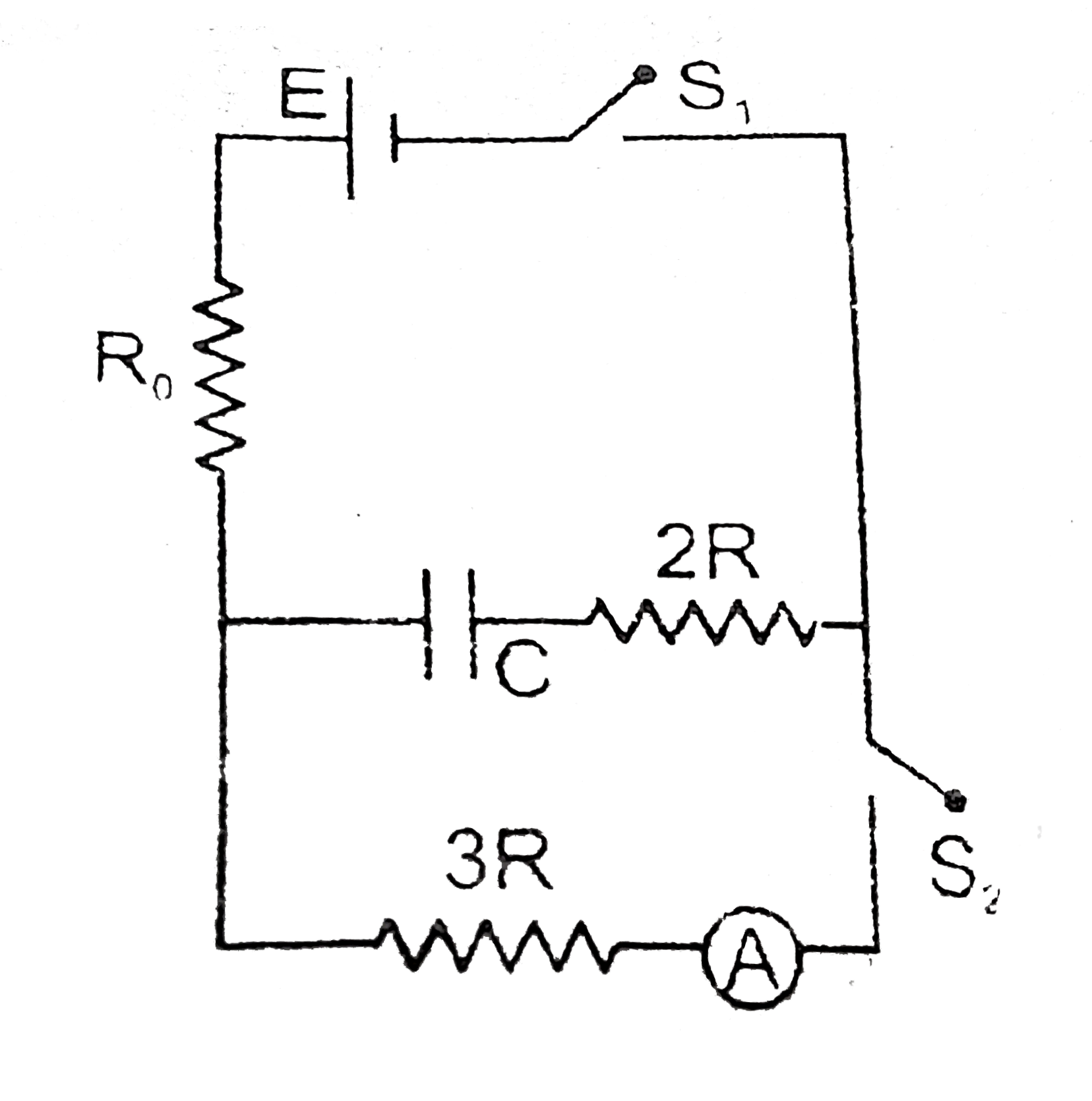
View SolutionThe capacitor 'C' is initially unchanged. Switch S1 is closed for a long time while S2 remains open. Now at t=0S2 is closed while S1 is opened. All the batteries are ideal and connecting wires are resistanceless
View Solution
