A point charges Q is moving in a circular orbit of radius R in the x-y plane with an angular velocity ω. This can be considered as equivalent to a loop carrying a steady current Qω2π. S uniform magnetic field along the positive z-axis is now switched on, which increases at a constant rate from 0 to B in one second. Assume that the radius of the orbit remains constant. The application of the magnetic field induces an EMF in the orbit. The induced EMF is defined as the work done by an induced electric field in moving a unit positive charge around a closed loop. It is known that, for an orbiting charge, the magnetic dipole moment is proportional to the angular momentum with a proportionality constant λ. The charge in the magnetic dipole moment associated with the orbit, at the end of the time interval of the magnetic field charge, is
λBQR2
−λBQR22
λBQR22
−λBQR2
The correct Answer is:B
To solve the problem, we need to determine the change in the magnetic dipole moment associated with a point charge Q moving in a circular orbit of radius R when a uniform magnetic field is switched on and increases at a constant rate.
1. Identify the Current Equivalent:
The point charge Q moving in a circular orbit can be treated as a current loop. The current I can be expressed as:
I=QT=Qω2π
where T is the period of one complete revolution, which is T=2πω.
2. Magnetic Dipole Moment:
The magnetic dipole moment m for a current loop is given by:
m=I⋅A
where A is the area of the loop. For a circular loop of radius R:
A=πR2
Therefore, substituting the expression for I:
m=(Qω2π)⋅πR2=QωR22
3. Change in Magnetic Field:
The magnetic field B is switched on and increases from 0 to B in 1 second. The rate of change of the magnetic field dBdt is:
dBdt=B1 s=B
4. Induced EMF:
According to Faraday's law of electromagnetic induction, the induced EMF E in the loop is given by:
E=−dΦdt
where Φ is the magnetic flux. The change in magnetic flux Φ through the loop is:
Φ=B⋅A=B⋅πR2
Therefore, the induced EMF becomes:
E=−ddt(B⋅πR2)=−πR2⋅dBdt=−πR2B
5. Change in Angular Momentum:
The angular momentum L of the charge in the orbit is given by:
L=mR2ω
The change in angular momentum due to the induced EMF can be expressed as:
ΔL=λΔm
where λ is a proportionality constant.
6. Change in Magnetic Dipole Moment:
The change in the magnetic dipole moment Δm can be expressed as:
Δm=λ⋅QBR22
Thus, the final expression for the change in the magnetic dipole moment is:
Δm=−λBQR22
The negative sign indicates that the induced magnetic dipole moment opposes the change in the magnetic field, in accordance with Lenz's law.
Final Answer:
The change in the magnetic dipole moment associated with the orbit at the end of the time interval of the magnetic field change is:
Δm=−λBQR22
The point charge Q moving in a circular orbit can be treated as a current loop. The current I can be expressed as:
I=QT=Qω2π
where T is the period of one complete revolution, which is T=2πω.
The magnetic dipole moment m for a current loop is given by:
m=I⋅A
where A is the area of the loop. For a circular loop of radius R:
A=πR2
Therefore, substituting the expression for I:
m=(Qω2π)⋅πR2=QωR22
The magnetic field B is switched on and increases from 0 to B in 1 second. The rate of change of the magnetic field dBdt is:
dBdt=B1 s=B
According to Faraday's law of electromagnetic induction, the induced EMF E in the loop is given by:
E=−dΦdt
where Φ is the magnetic flux. The change in magnetic flux Φ through the loop is:
Φ=B⋅A=B⋅πR2
Therefore, the induced EMF becomes:
E=−ddt(B⋅πR2)=−πR2⋅dBdt=−πR2B
The angular momentum L of the charge in the orbit is given by:
L=mR2ω
The change in angular momentum due to the induced EMF can be expressed as:
ΔL=λΔm
where λ is a proportionality constant.
The change in the magnetic dipole moment Δm can be expressed as:
Δm=λ⋅QBR22
Thus, the final expression for the change in the magnetic dipole moment is:
Δm=−λBQR22
The negative sign indicates that the induced magnetic dipole moment opposes the change in the magnetic field, in accordance with Lenz's law.
The change in the magnetic dipole moment associated with the orbit at the end of the time interval of the magnetic field change is:
Δm=−λBQR22
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Archives (integer)2videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Subective Type2videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Archives (multiple Correct)3videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
Similar Questions
A point charges Q is moving in a circular orbit of radius R in the x-y plane with an angular velocity ω. This can be considered as equivalent to a loop carrying a steady current Qω2π. S uniform magnetic field along the positive z-axis is now switched on, which increases at a constant rate from 0 to B in one second. Assume that the radius of hte orbit remains constant. The application of hte magnetic field induces an emf in the orbit. The induced emf is defined as the work done by an induced electric field in moving a unit positive charge around a closed loop. It si known that, for an orbiting charge, the magnetic dipole moment is proportional to the angular momentum with a porportionality constant λ.
The charge in the magnetic dipole moment associated with the orbit. at the end of the time interval of hte magnetic field charge, isView SolutionA point charges Q is moving in a circular orbit of radius R in the x-y plane with an angular velocity ω. This can be considered as equivalent to a loop carrying a steady current Qω2π. S uniform magnetic field along the positive z-axis is now switched on, which increases at a constant rate from 0 to B in one second. Assume that the radius of hte orbit remains constant. The application of hte magnetic field induces an emf in the orbit. The induced emf is defined as the work done by an induced electric field in moving a unit positive charge around a closed loop. It si known that, for an orbiting charge, the magnetic dipole moment is proportional to the angular momentum with a porportionality constant λ.
The magnitude of the induced electric field in the orbit at any instant of time during the time interval of the mangnetic field change isView SolutionA point charges Q is moving in a circular orbit of radius R in the x-y plane with an angular velocity ω. This can be considered as equivalent to a loop carrying a steady current Qω2π. S uniform magnetic field along the positive z-axis is now switched on, which increases at a constant rate from 0 to B in one second. Assume that the radius of hte orbit remains constant. The application of hte magnetic field induces an emf in the orbit. The induced emf is defined as the work done by an induced electric field in moving a unit positive charge around a closed loop. It si known that, for an orbiting charge, the magnetic dipole moment is proportional to the angular momentum with a porportionality constant λ.
The magnitude of the induced electric field in the orbit at any instant of time during the time interval of the mangnetic field change isView SolutionA particle of charge q and mass m moves in a circular orbit of radius r with angular speed ω. The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
View SolutionA particle of charge q and mass m moves in a circular orbit of radius r with angular speed ω. The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
View SolutionAn electron moving in a circular orbit of radius R with frequency f. The magnetic field at the centre of the orbit is
View SolutionA semicircular loop of radius R is rotated with an angular velocity ω perpendicular to the plane of a magnetic field B as shown in the figure. Emf Induced in the loop is
 View Solution
View SolutionA circular loop carrying a current I is placed in the xy-plane as shown in figure. A uniform magnetic fied B is oriented along the positive z-axis. The loop tends to
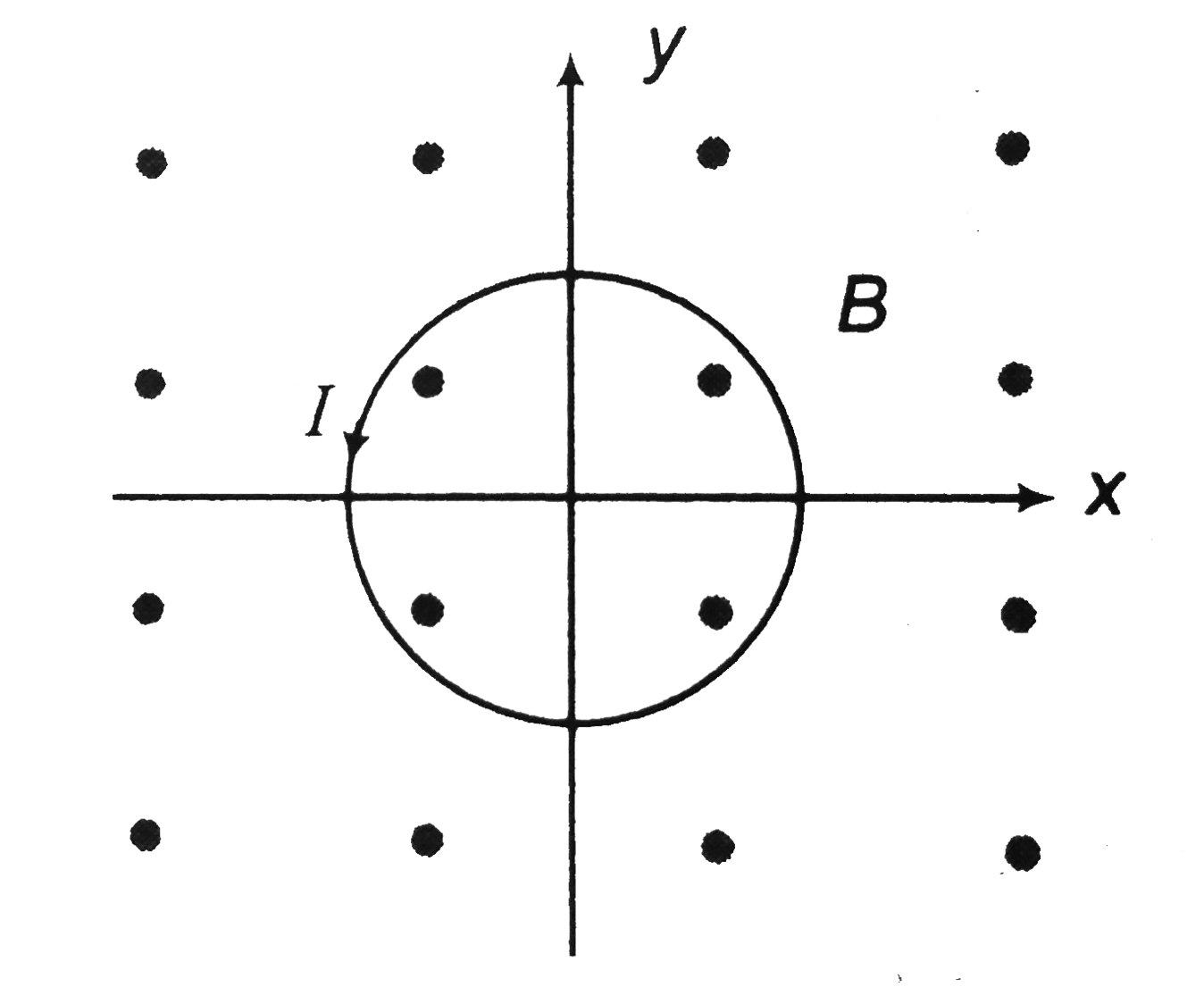 View Solution
View SolutionA charge q is spread uniformly over an insulated loop of radius r. If it is rotated with an angular velocity ω with respect to normal axis then the magnetic moment of the loop is :
View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.
 View Solution
View Solution

