The half cycle of an alternating singnal is shown in fig. It increases uniformly form zero at 0∘→Fmat(α)∘ and decrease uniformly from (Fm)at180∘

The effective value of the singnal is
Fm√(1−4α3π)
Fm√(1+4α3π)
Fm√(1−3α4π)
Fm√(1+3α4π)
The correct Answer is:A
For finding the average value m, we would find the total area of the trapezium and divide it by (π).
Area=2×ΔOAE+rectang≤ABDE
=2×(1/2)×Fm0α+(π−2α)Fm0=(π−α)Fm
Average value =(π−α)Fm/(π)
rms value: From similar triangles , we get
ytˆa=Fmα or (y2)=F2mα2tˆa2
This gives the equation of the single over the two triangles OAE and DBC. The single reamins constant over the angle α to (π−α), i.e., over an angluar distance of (π−α)−α=(π−2α).
Sum of the square
2f2mα2F2m(π−4α3)
The mean value of the squares
=1πF2m(π−4α3)=F2m(1−4α3π)
rms value =Fm√(1−4α3π).
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Integer
4 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Archives Subjective
1 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Assertion-reasoning
7 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.3
15 Videos
Similar Questions
The half cycle of an alternating singnal is shown in fig. It increases uniformly form zero at 0∘→Fmat(α)∘ and decrease uniformly from (Fm)at180∘

The average value of the singnal is
View SolutionThe time required for a 50 Hz sinusoidal alternating current to changed its value from zero to the r.m.s. value
View Solution
Knowledge Check
A coil having an inductance of 0.5 H carries a current which is uniformly varying from zero to 10 ampere in 2 second. The e.m.f. (in volts) generated in the coil is
A10B5C2.5D1.25
If the current in the toroidal solenoid increases uniformly from zero to 6.0 A in 3.0μs Self-inductance of the toroidal solenoid is 40μ H The magnitude of self-induced emf is
View SolutionA particle of mass m moving with a velocity u makes an elastic one-dimensional collision with a stationary particle of mass m establishing a contact with it for extermely small time. T. Their force of contact increases from zero to F0 linearly in time T/4, remains constant for a further time T/2 and decreases linearly from F0 to zero in further time T/4 as shown. The magnitude possessed by F0 is.
 .
.
View SolutionA particle of mass m moving with a velocity u makes an elastic one-dimensional collision with a stationary particle of mass m establishing a contact with it for extermely small time. T. Their force of contact increases from zero to F0 linearly in time T/4, remains constant for a further time T/2 and decreases linearly from F0 to zero in further time T/4 as shown. The magnitude possessed by F0 is.
 .
.
View SolutionA particle of mass m moving with velocity u makes an elastic one-dimentional collision with a stationary particle of mass m. They come in contact for a very small time t0. Their force of interaction increases from zero to F0 linearly in time 0.5t0, and decreases linearly to zero in further time 0.5t0 as shown in figure. The magnitude of F0 is
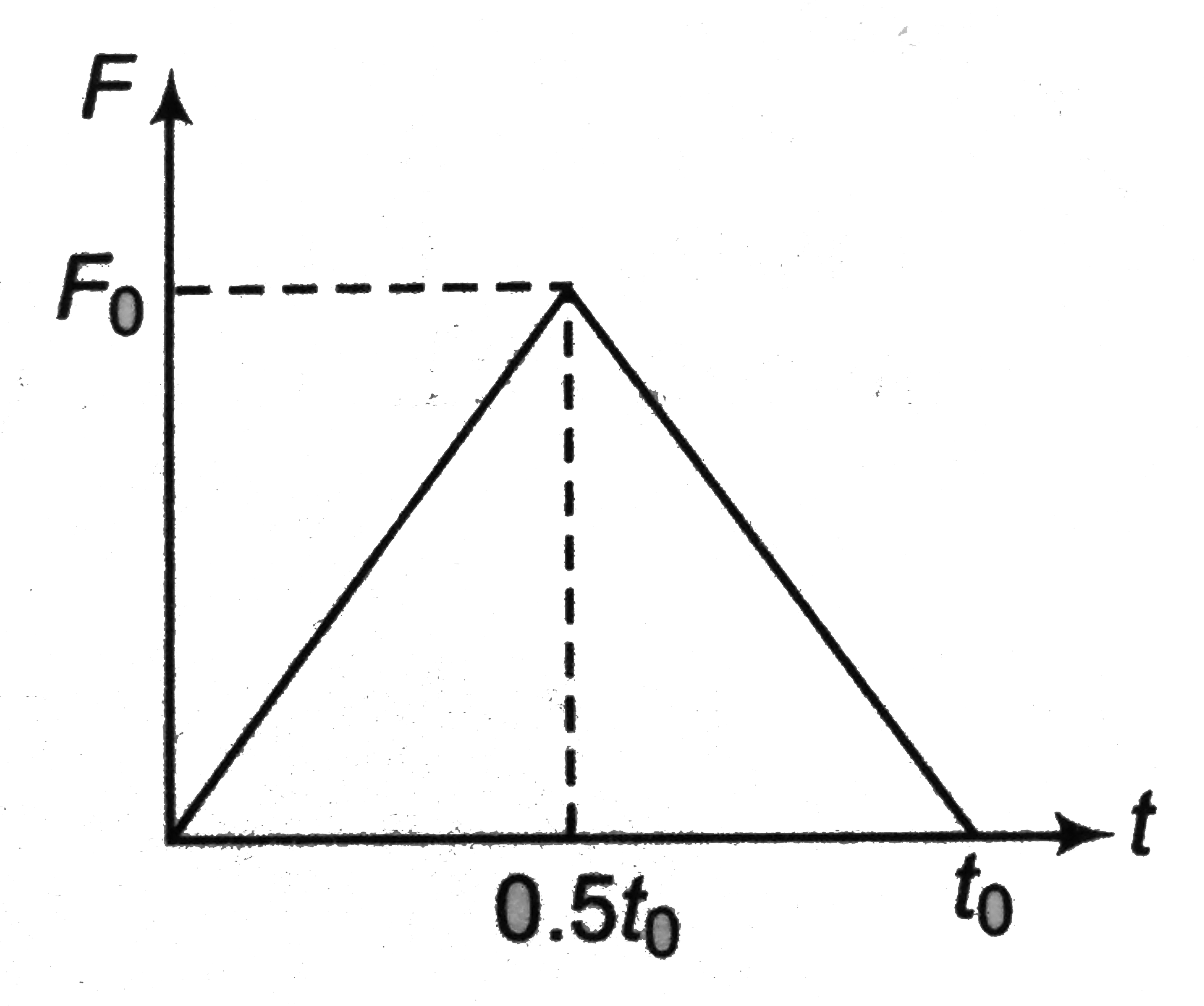
View SolutionA particle of mass m moving with velocity u makes an elastic one-dimensional collision with a stationary particle of mass m. They come in contact for a very small time t0. Their force of interaction increases from zero to F0 linearly in time 0.5t0, and decreases linearly to zero in further time 0.5t0 as shown in figure. The magnitude of F0 is

View SolutionIf the velocity v of a particle moving along a straight line decreases linearly with its displacement from 20m/s to a value approaching zero at s=30m, determine the acceleration of the particle when s=15m.
View SolutionIf the velocity v of a particle moving along a straight line decreases linearly with its position coordinates s from 50m/s to a value approaching zero at = 100 m, the time it takes to reach the 100 m position will be:
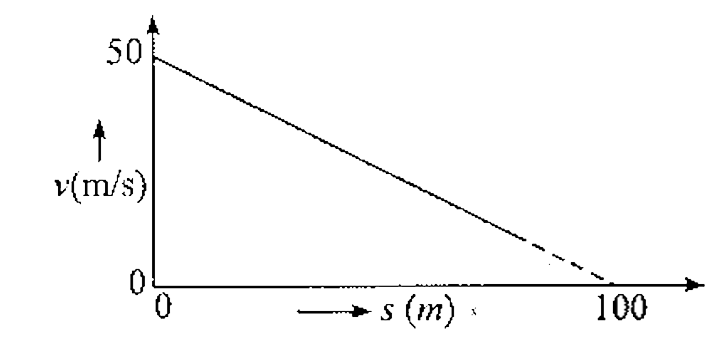
View Solution
