Your clock radio awakens you with a steady and irritating sound of frequency 600 Hz. On morning, it malfunction and cannot be turned off. In frustration, you drop the clock radio out of your fourth-story dorm wndow 15.0m from the ground. Assume the speed of sound is 343 m/s. As you listen to the falling clock radio, what frequency do you hear just before you hear it striking the ground?
To solve the problem step by step, we will follow these calculations:
Step 1: Identify the given values
- Frequency of the clock radio (source frequency, f) = 600 Hz
- Height from which the clock radio is dropped (distance, s) = 15.0 m
- Acceleration due to gravity (g) = 10 m/s² (approximately)
- Speed of sound in air (v) = 343 m/s
Step 2: Calculate the velocity of the falling clock radio just before it hits the ground
We will use the kinematic equation:
v2=u2+2as
Where:
- v = final velocity of the clock radio
- u = initial velocity (0 m/s, since it is dropped)
- a = acceleration (10 m/s²)
- s = distance (15 m)
Substituting the values:
v2=0+2×10×15
v2=300
v=√300≈17.32m/s
Step 3: Use the Doppler Effect formula to find the observed frequency
Since the clock radio is falling (moving away from the observer), we use the formula for the Doppler Effect:
f′=vv+vs⋅f
Where:
- f′ = observed frequency
- vs = velocity of the source (clock radio) = 17.32 m/s
- f = source frequency = 600 Hz
Substituting the values:
f′=343343+17.32⋅600
Calculating the denominator:
343+17.32=360.32
Now substituting back into the equation:
f′=343360.32⋅600
Calculating the fraction:
f′≈0.952⋅600≈571.2Hz
Step 4: Final Answer
The frequency you hear just before the clock radio strikes the ground is approximately 571 Hz.
---
- Frequency of the clock radio (source frequency, f) = 600 Hz
- Height from which the clock radio is dropped (distance, s) = 15.0 m
- Acceleration due to gravity (g) = 10 m/s² (approximately)
- Speed of sound in air (v) = 343 m/s
We will use the kinematic equation:
v2=u2+2as
Where:
- v = final velocity of the clock radio
- u = initial velocity (0 m/s, since it is dropped)
- a = acceleration (10 m/s²)
- s = distance (15 m)
v2=0+2×10×15
v2=300
v=√300≈17.32m/s
Since the clock radio is falling (moving away from the observer), we use the formula for the Doppler Effect:
f′=vv+vs⋅f
Where:
- f′ = observed frequency
- vs = velocity of the source (clock radio) = 17.32 m/s
- f = source frequency = 600 Hz
f′=343343+17.32⋅600
Calculating the denominator:
343+17.32=360.32
Now substituting back into the equation:
f′=343360.32⋅600
Calculating the fraction:
f′≈0.952⋅600≈571.2Hz
The frequency you hear just before the clock radio strikes the ground is approximately 571 Hz.
Topper's Solved these Questions
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Examples
56 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Exercise 6.1
56 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type
5 Videos
Similar Questions
The sound level at a distance of 3.00 m from a source is 120 dB. At what distance will the sound level be (a) 100 dB and (b) 10.0 dB?
View SolutionDo displacement particle velocity and pressure variation in a longitudinal wave vary with the same phase?
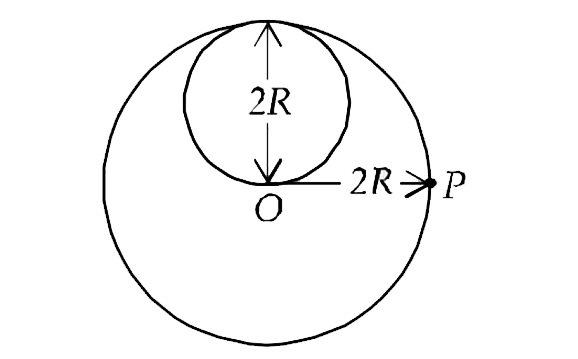
View SolutionA lamina is made by removing a small disc of diameter 2R from a bigger disc of uniform mass density and radius 2R, as shown in the figure. The moment of inertia of this lamina about axes passing though O and P is IOandIP respectively. Both these axes are perpendicular to the plane of the lamina. The ratio IPIO is
View SolutionA string of length L, fixed at its both ends is vibrating in its 1st overtone mode. Consider two elements of the string of the same small length at positions l1=0.2Landl2=0.45L from one end.
If K1andK2 are their respective maximum kinetic energies,then
View SolutionIf you are walking on the moon, can you hear the sound of stones cracking behind you ? Can you hear the sound of your own footsteps ?
View SolutionA siren emitting a sound of frequency 1000HZ moves away from you towards a cliff at a speed of 10m/s .
(a) What is the frequency of the sound you hear coming directly from the sirven ?
(b) What is the frequency of sounds you hear reflected off the cliffb ?
(c) What beat frequency would you hear ? Take the speed of sound in air as 330m/s .
View SolutionYour clock radio awakens you with a steady and irritating sound of frequency 600 Hz. On morning, it malfunction and cannot be turned off. In frustration, you drop the clock radio out of your fourth-story dorm wndow 15.0m from the ground. Assume the speed of sound is 343 m/s. As you listen to the falling clock radio, what frequency do you hear just before you hear it striking the ground?
View SolutionA siren emitting a sound of frequency 2000 Hz moves away from you towards a cliff at a speed of 8 m/s. (a) What is the frequency of the sound you hear coming directly from the siren. (b) What is the frequency of sound you hear reflected off the cliff. Speed of sound in air is 330(m)/(s) .
View Solutionआपके रेडियों एरियल पर सभी स्टेशनों से प्रसारित तरंगें आती हैं परन्तु आपको एक बार में एक ही स्टेशन का कार्यक्रम सुनाई देता है , क्यों ?
View SolutionDo you hear any sound?
View SolutionIf you are walking on the moon, can you hear the sound of stones cracking behind you ? Can you hear the sound of your own footsteps ?
View SolutionA siren emitting a sound of frequency 1000 Hz moves away from you towards a cliff at a speed of 10 m/s. (a) What is the frequency of the sound you hear coming directly from the siren ? (b) What is the frequency of the sound you hear reflected off the cliff (c) What beat frequency would you hear ? Take the speed of sound in air as, 330 m/s.
View SolutionSuppose you and your friend are on the moon. Will you be able to hear any sound
View SolutionA siren emitting a sound of frequency 1000 H_(Z) moves away from you towards a cliff at a speed of 10 m//s . (a) What is the frequency of the sound you hear coming directly from the sirven ? (b) What is the frequency of sounds you hear reflected off the cliffb ? (c) What beat frequency would you hear ? Take the speed of sound in air as 330 m//s .
View SolutionA siren emitting a sound of frequency 2000 Hz moves away from you towards a cliff at a speed of 8 m/s. (a) What is the frequency of the sound you hear coming directly from the siren. (b) What is the frequency of sound you hear reflected off the cliff. Speed of sound in air is 330(m)/(s) .
View Solution
