A submarin Travels through water at a speed of 8.00ms, emitting a sonar wave at a frequency of 1400 Hz. The speed of sound in the water is 1533 m/s. What frequency is detected by an observer riding on submarine of velocity 9.00msas the submarines approach each other?
To solve the problem of finding the frequency detected by an observer riding on a submarine as both submarines approach each other, we can use the Doppler effect formula for sound waves. Here’s a step-by-step solution:
Step 1: Identify the given values
- Speed of the first submarine (source, vs) = 8.00 m/s (moving towards the observer)
- Speed of the second submarine (observer, vo) = 9.00 m/s (also moving towards the source)
- Frequency of the sonar wave emitted by the source (f) = 1400 Hz
- Speed of sound in water (v) = 1533 m/s
Step 2: Determine the direction of velocities
Since both submarines are approaching each other, the velocities will be added in the Doppler effect formula:
- The velocity of the observer (vo) is positive because it is moving towards the source.
- The velocity of the source (vs) is also subtracted from the speed of sound because it is moving towards the observer.
Step 3: Use the Doppler effect formula
The Doppler effect formula for frequency detected by a moving observer when the source is also moving is given by:
f′=f×v+vov−vs
Where:
- f′ = frequency detected by the observer
- f = frequency emitted by the source
- v = speed of sound in the medium
- vo = speed of the observer
- vs = speed of the source
Step 4: Substitute the values into the formula
Substituting the known values into the formula:
f′=1400Hz×1533m/s+9m/s1533m/s−8m/s
Step 5: Calculate the numerator and denominator
Calculate the numerator:
v+vo=1533+9=1542m/s
Calculate the denominator:
v−vs=1533−8=1525m/s
Step 6: Plug the values back into the equation
Now, substituting these values back into the equation:
f′=1400Hz×15421525
Step 7: Perform the calculation
Calculating the fraction:
15421525≈1.0111
Now multiply by the frequency:
f′≈1400×1.0111≈1415.54Hz
Step 8: Round to appropriate significant figures
Rounding to three significant figures, we get:
f′≈1416Hz
Final Answer
The frequency detected by the observer is approximately 1416 Hz.
---
- Speed of the first submarine (source, vs) = 8.00 m/s (moving towards the observer)
- Speed of the second submarine (observer, vo) = 9.00 m/s (also moving towards the source)
- Frequency of the sonar wave emitted by the source (f) = 1400 Hz
- Speed of sound in water (v) = 1533 m/s
Since both submarines are approaching each other, the velocities will be added in the Doppler effect formula:
- The velocity of the observer (vo) is positive because it is moving towards the source.
- The velocity of the source (vs) is also subtracted from the speed of sound because it is moving towards the observer.
The Doppler effect formula for frequency detected by a moving observer when the source is also moving is given by:
- f′ = frequency detected by the observer
- f = frequency emitted by the source
- v = speed of sound in the medium
- vo = speed of the observer
- vs = speed of the source
Substituting the known values into the formula:
Calculate the numerator:
Now, substituting these values back into the equation:
Calculating the fraction:
Rounding to three significant figures, we get:
The frequency detected by the observer is approximately 1416 Hz.
Topper's Solved these Questions
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Examples
56 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Exercise 6.1
56 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type
5 Videos
Similar Questions
The sound level at a distance of 3.00 m from a source is 120 dB. At what distance will the sound level be (a) 100 dB and (b) 10.0 dB?
View SolutionDo displacement particle velocity and pressure variation in a longitudinal wave vary with the same phase?
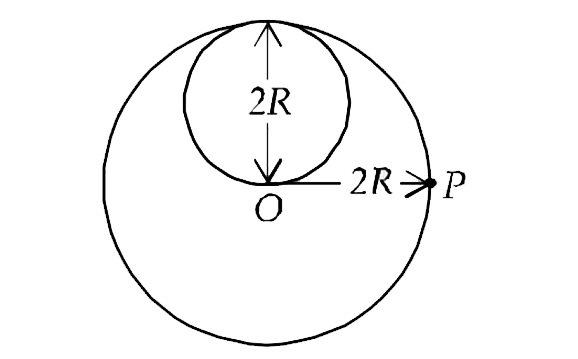
View SolutionA lamina is made by removing a small disc of diameter 2R from a bigger disc of uniform mass density and radius 2R, as shown in the figure. The moment of inertia of this lamina about axes passing though O and P is IOandIP respectively. Both these axes are perpendicular to the plane of the lamina. The ratio IPIO is
View SolutionA string of length L, fixed at its both ends is vibrating in its 1st overtone mode. Consider two elements of the string of the same small length at positions l1=0.2Landl2=0.45L from one end.
If K1andK2 are their respective maximum kinetic energies,then
View SolutionTwo submarines are approaching each other in a calm sea. The first submarine travels at a speed of 36kmh−1 and the other at 54kmh−1 relative to the water. The first submarine sends a sound signal (sound waves in water are also called sonar) at a frequency of 2000 Hz. (a) At what frequency is this signal received by the second submarine ? (b) The signal is reflected from the second submarine. At what frequency is this signal received by the first submarine. Take the speed of the sound wave in water to be 1500ms−1 .
View SolutionA submarin Travels through water at a speed of 8.00(m)/(s) , emitting a sonar wave at a frequency of 1400 Hz. The speed of sound in the water is 1533 m/s. What frequency is detected by an observer riding on sub as the submarines approach each other?
View SolutionA sonar system fixed in a submarine operates at a frequency 40.0 kHz, An enemy subarine moves towords the sonar with a speed of 360 km/h. What is the frequency of sound refielcted by the submarine? (Take the speed of sound in water to be 1450 m/s)
View SolutionA SONAR system fixed in a submarine operates at a frequency 50 kHz. It is moving towards a rocky hill present inside water with a speed of 432 km h^(-1) . What is the apparent frequency of sound observed at the submarine after reflection by the rocky hill ? (Take velocity of sound in water to be 1450 m s^(-1) )
View Solutionजल के नीचे वस्तुओं को ढूंढने व उनके स्थान का पता लगाने के लिए सोनार ( SONAR ) में पराश्रव्य तरंगों का प्रयोग होता है । कोई पनडुब्बी सोनार से सुसज्जित है । इसके द्वारा जनित अन्वेषी तरंग और शत्रु की पनडुब्बी से परिवर्तित इसकी प्रतिध्वनि की प्राप्ति के बीच काल विलंब 77.0 s है । शत्रु की पनडुब्बी कितनी दूर है ? (जल में ध्वनि की चाल =1450ms−1) ।
View Solutionकिसी पनडुब्बी से आबद्ध कोई 'सोनार' निकाय 40.0 kHz आवृत्ति पर प्रचालन करता है । कोई शत्रु - पनडुब्बी (340km/h) चाल से इस सोनार की ओर गति करती है । पनडुब्बी से परावर्तित ध्वनि की आवृत्ति क्या है ? जल में ध्वनि की चाल (1450m/s) लिजिए ।
View Solutionजल के नीचे वस्तुओ को ढूढ़ने व उनके स्थान का पता लगाने के लिए सोनार (SONAR) में पराश्रव्य तरंगो का प्रयोग होता है । कोई पनडुब्बी सोनार से सुसज्जित है । इसके द्वारा जनित अन्वेषी तरंग और शत्रु की पनडुब्बी से प्रवर्तित इसकी प्रतिध्वनि की प्राप्ति के बीच काल विलम्ब 77.0 s है । शत्रु की पनडुब्बी कितनी दूर है ? (जल में ध्वनि की चाल = 1450 m s−1) |
View Solutionदो पनडुब्बियाँ एक समुंद्र के अंदर शांत जल में एक-दूसरे की ओर चल रही हैं । पानी के सापेक्ष पहली पनडुब्बी की चाल 36 km/h तथा दूसरी की चाल 54 km/h है । पहली पनडुब्बी 2000 Hz आवृति वाला एक ध्वनि सिग्नल भेजती है । (a) दूसरी पनडुब्बी इस सिग्नल को किस आवृति के साथ प्राप्त करेगी ? (b) दूसरी पनडुब्बी से परावर्तित होकर आ रहे सिग्नल को पहली पनडुब्बी की किस आवृति के साथ प्राप्त करेगी ? पानी में ध्वनि का वेग 1500 m/s है ।
View SolutionA SONAR system fixed in a submarine operates at a frequency40.0 kHz. An enemy submarine moves towards the SONAR with a speed of 360km h^(-1) .What is the frequency of sound reflected by the submarine? Take the speed of sound in water to be 1450ms^(-1)
View Solutionकिसी पनडुब्बी से आबद्ध कोई सोनार निकाय 40.0 किलोहर्ट्ज आवृत्ति पर प्रचालन करता है। कोई शत्रु-पनडुब्बी 360 किमी/घण्टा चाल से इस सोनार की ओर गति करती है। पनडुब्बी से परावर्तित ध्वनि की आवृत्ति क्या है? जल में ध्वनि की चाल 1450 मीटर/सेकण्ड लीजिए।
View Solutionएक पनडुब्बी सोनार संकेत उत्सर्जित करती है जो समुद्र के जल के अंदर एक चट्टान से टकराकर 1.02 s के बाद पनडुब्बी पर वापस लौटती है। यदि समुद्री जल में ध्वनि की चाल 1530 m/s हो, तो पनडुब्बी से चट्टान की दुरी निकालिए ।
View SolutionA sonar system fixed in a submarine operates at a frequency 40.0 kHz. An enemy submarine moves towards the sonar with a speed of 360kmh−1. What is the frequency of sound reflected by the submarine ? Take the speed of sound in water to be 1450ms−1
View Solution
