Find the molecular weight for a gas in which the velocity of sound is 1260ms at 0∘C and whose γ is 1.4.
C=√γPρ
1260=√1.4Pρ
Pρ of the gas at 0∘C=11.34×105
P=ρMRT is the perfect gas equation in terms of density
Pρ=RTM
M=8.3×27311.34×105=2×10−3kg=2g
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Exercise 6.272videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Subjective56videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Examples56videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type5videos
SUPERPOSITION AND STANDING WAVES
Similar Questions
Find the temperature at which the velocity of sound in air will be 112 times of the velocity at 27∘C.
View SolutionFind the temperature at which the velocity of sound in air is double the velocity of sound in air at 0∘C.
[Hint : Use CC0=√TT0]View SolutionIf cs is the velocity of sound in air and c is rms velocity , then
View SolutionCalculate the molecular weight of a gas X which diffuses four times as fast as another gas Y, which in turn diffuses twice as fast as another Z. Molecular weight of the gas Z is 128.
View SolutionCalculate the molecular weight of a gas which diffuses four times as fast as another gas Y, which in turn diffuses twice as fast as another gas Z [All under identical conditions]. Molecules weight of Z is 128.
View Solution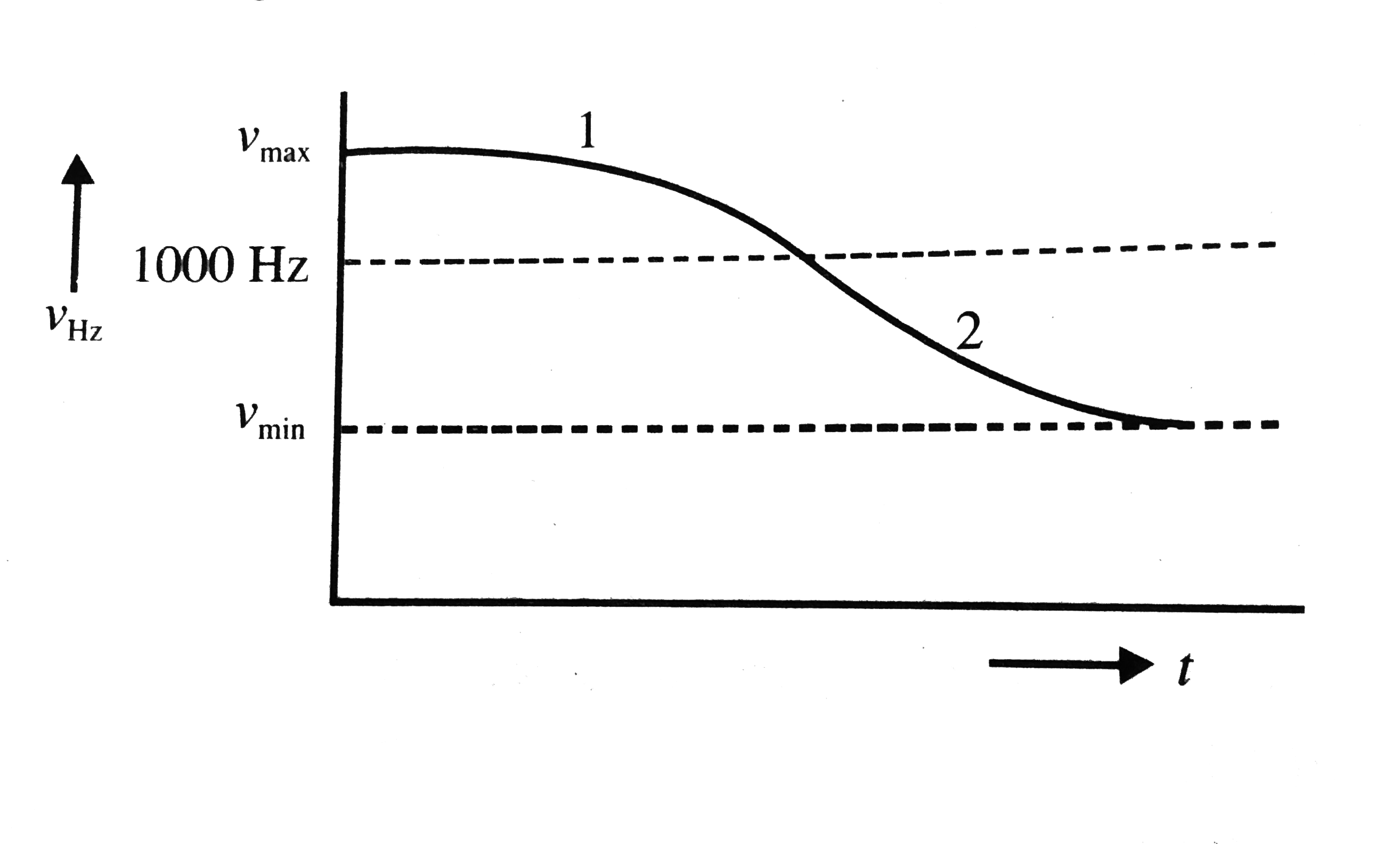
A stationary observer receives a sound from a sound of freqeuency v0 moving with a constant velocity vS=30ms The apparent frequency varies with time as shown in figure. Velocity of sound v=300ms. Then which of the following is incorrect?View Solution-
A stationary observer receives a sound from a sound of freqeuency v0 moving with a constant velocity vS=30ms The apparent frequency varies with time as shown in figure. Velocity of sound v=300ms. Then which of the following is incorrect?View Solution Calculate the increase in velocity of sound for 1∘C rise of temperature if the velocity of sound at 0∘C is 332m/s.
View SolutionFind the velocity of sound in O2 at NTP. Given that the velocity of sound in the H2 at NTP is 1880ms−1 the density of oxygen is 16 times the density of hydrogen γ=1.4 for both the gases.
View SolutionThe molecules of a given mass of gas have an rms velocity of 200ms−1 at 27∘C and pressure 1 atm. When the temperature is 127∘C and pressure is 2 atm, the rms velocity in ms−1 will be ?
View Solution