Two tuning forks A and B having a frequency of 500 Hz each are placed with B to the right of A. An observer in between the forks in moving towards B with a speed of 25 m/s. The speed of sound is 345 m/s and the wind speed is 5 m/s from A to B. Calculate the difference in the two frequencies heard by observer.
To solve the problem of finding the difference in frequencies heard by the observer moving towards tuning fork B, we will use the Doppler effect formula. Here’s the step-by-step solution:
Step 1: Identify the given values
- Frequency of tuning forks (A and B), f0=500Hz
- Speed of sound, v=345m/s
- Speed of wind, vw=5m/s (from A to B)
- Speed of observer, vo=25m/s
Step 2: Calculate the apparent frequency of tuning fork A
The observer is moving towards tuning fork B and away from tuning fork A. The effective speed of sound when considering the wind is:
- For tuning fork A: v+vw=345+5=350m/s
Using the Doppler effect formula for a source at rest and an observer moving away:
f′A=f0(v+vwv+vo)
Substituting the values:
f′A=500(350345+25)=500(350370)
Calculating:
f′A=500×0.945=472.5Hz
Step 3: Calculate the apparent frequency of tuning fork B
For tuning fork B, the observer is moving towards it, and the wind is blowing in the same direction as the sound:
- For tuning fork B: v−vw=345−5=340m/s
Using the Doppler effect formula:
f′B=f0(v−vwv−vo)
Substituting the values:
f′B=500(340345−25)=500(340320)
Calculating:
f′B=500×1.0625=531.25Hz
Step 4: Calculate the difference in frequencies
Now, we find the difference in frequencies heard by the observer:
Δf=f′B−f′A=531.25−472.5=58.75Hz
Final Answer
The difference in the two frequencies heard by the observer is 58.75 Hz.
---
- Frequency of tuning forks (A and B), f0=500Hz
- Speed of sound, v=345m/s
- Speed of wind, vw=5m/s (from A to B)
- Speed of observer, vo=25m/s
The observer is moving towards tuning fork B and away from tuning fork A. The effective speed of sound when considering the wind is:
- For tuning fork A: v+vw=345+5=350m/s
f′A=f0(v+vwv+vo)
Substituting the values:
f′A=500(350345+25)=500(350370)
Calculating:
f′A=500×0.945=472.5Hz
For tuning fork B, the observer is moving towards it, and the wind is blowing in the same direction as the sound:
- For tuning fork B: v−vw=345−5=340m/s
f′B=f0(v−vwv−vo)
Substituting the values:
f′B=500(340345−25)=500(340320)
Calculating:
f′B=500×1.0625=531.25Hz
Now, we find the difference in frequencies heard by the observer:
Δf=f′B−f′A=531.25−472.5=58.75Hz
The difference in the two frequencies heard by the observer is 58.75 Hz.
Topper's Solved these Questions
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICS ENGLISHChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Subjective
Explore 56 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICS ENGLISHChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Single Correct
Explore 252 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICS ENGLISHChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Exercise 6.1
Explore 56 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Interger
Explore 2 Videos
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICS ENGLISHChapter:SUPERPOSITION AND STANDING WAVESExercise:Comprehension Type
Explore 5 Videos
Similar Questions
Two train whistles A and B each have a frequency of 220 Hz. A is stationary and B is moving toward the right (away from A) at a speed of 35m/s . A listener between the two trains is moving towards the right with a speed of 15m/s . No wind is blowing.
What is frequency from A as heard by the listener
View SolutionA source of sound of frequency 500 Hz is moving towards an observer with velocity 30 m/s . The speed of sound is 330 m/s . the frequency heard by the observer will be
View SolutionTwo tuning forks with natural frequencies of 340Hz each move relative to a stationary observer. One fork moves away form the observer, while the other moves towards him at the same speed. The observer hears beats of frequency 3Hz. Find the speed of the tuning fork.
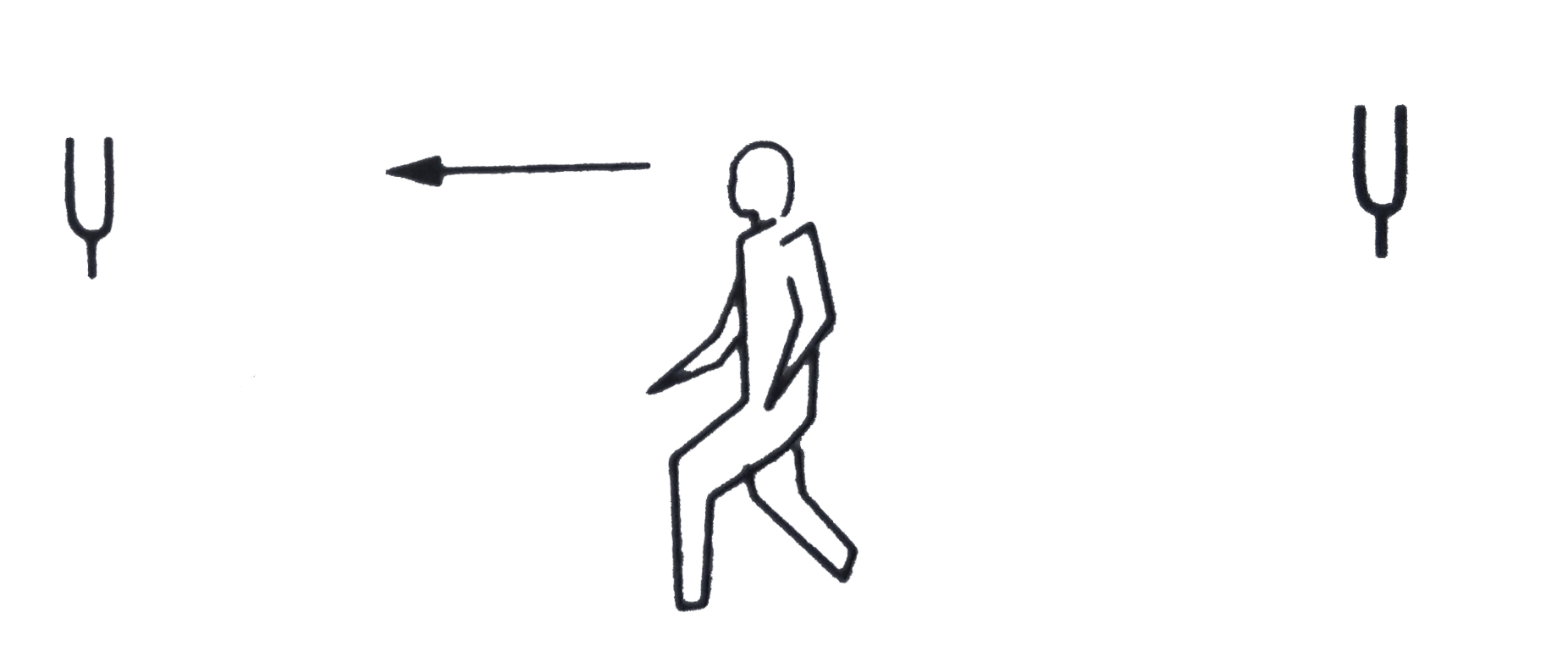
View SolutionTwo identical tuning forks vibrating at the same frequency 256 Hz are kept fixed at some distance apart. A listener runs between the forks at a speed of 3.0ms−1 so that he approaches one tuning-fork and recedes from the other. find the beat frequency observed by the listener. Speed of sound in air =332ms−1.
 .
.
View SolutionTwo tuning forks A and B lying on opposite sides of observer 'O' and of natural frequency 80Hz move with velocity 10m/s relative to stationary observer O. Fork A moves away from the observer while the fork B moves towards him. A wind with a speed 10m/s is blowing in the direction of motion of fork A. Find the beat frequency measured by the observer in Hz. [Take speed of sound in air as 340m/s].
View SolutionA tuning fork of frequency 256hZ is moving towards a well with a velocity of 5m/s . If the speed of sound is 330m/s , then the number of beats heard per second by a stationary observer lying between tuning fork and the well is
View Solution
As shown if Fig. a vibrating tuning fork of frequency 512 Hz is moving towards the wall with a speed 2ms. Take speed of sound as v=340ms and answer the following questions.
Q. If the listener is at rest and located such that the tuning fork is moving between the listener and the wall, number of beats heard by the listerner per second will be nearly
View Solution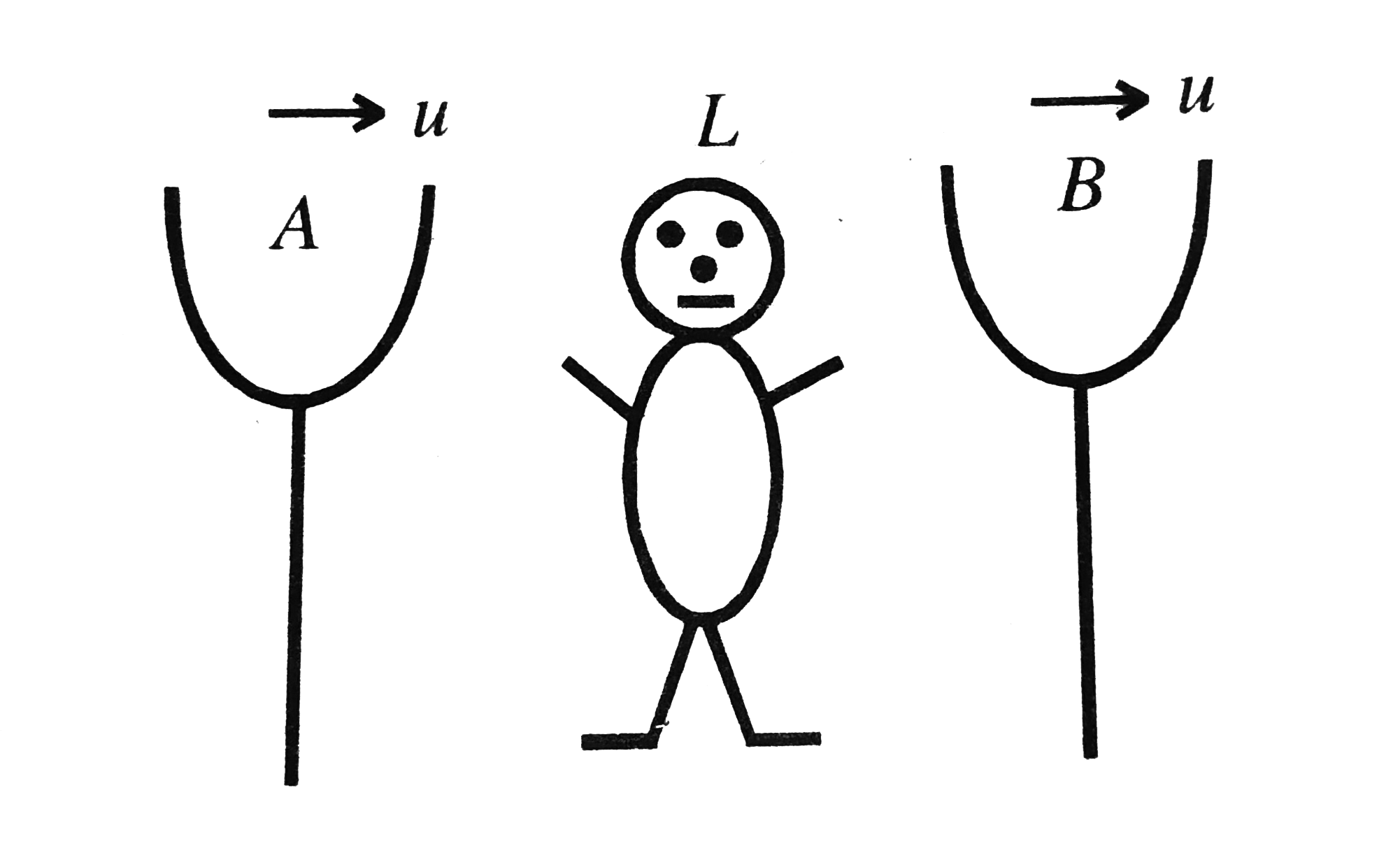 Two tuning forks A and B are vibrating at the same frequency 256 Hz. A listener is standing midway between the forks. If both tuning forks move to the right with a velocity of 5ms, find the number of beats heard per second by the listerner (speed of sound in air is 330ms).
Two tuning forks A and B are vibrating at the same frequency 256 Hz. A listener is standing midway between the forks. If both tuning forks move to the right with a velocity of 5ms, find the number of beats heard per second by the listerner (speed of sound in air is 330ms).
View Solution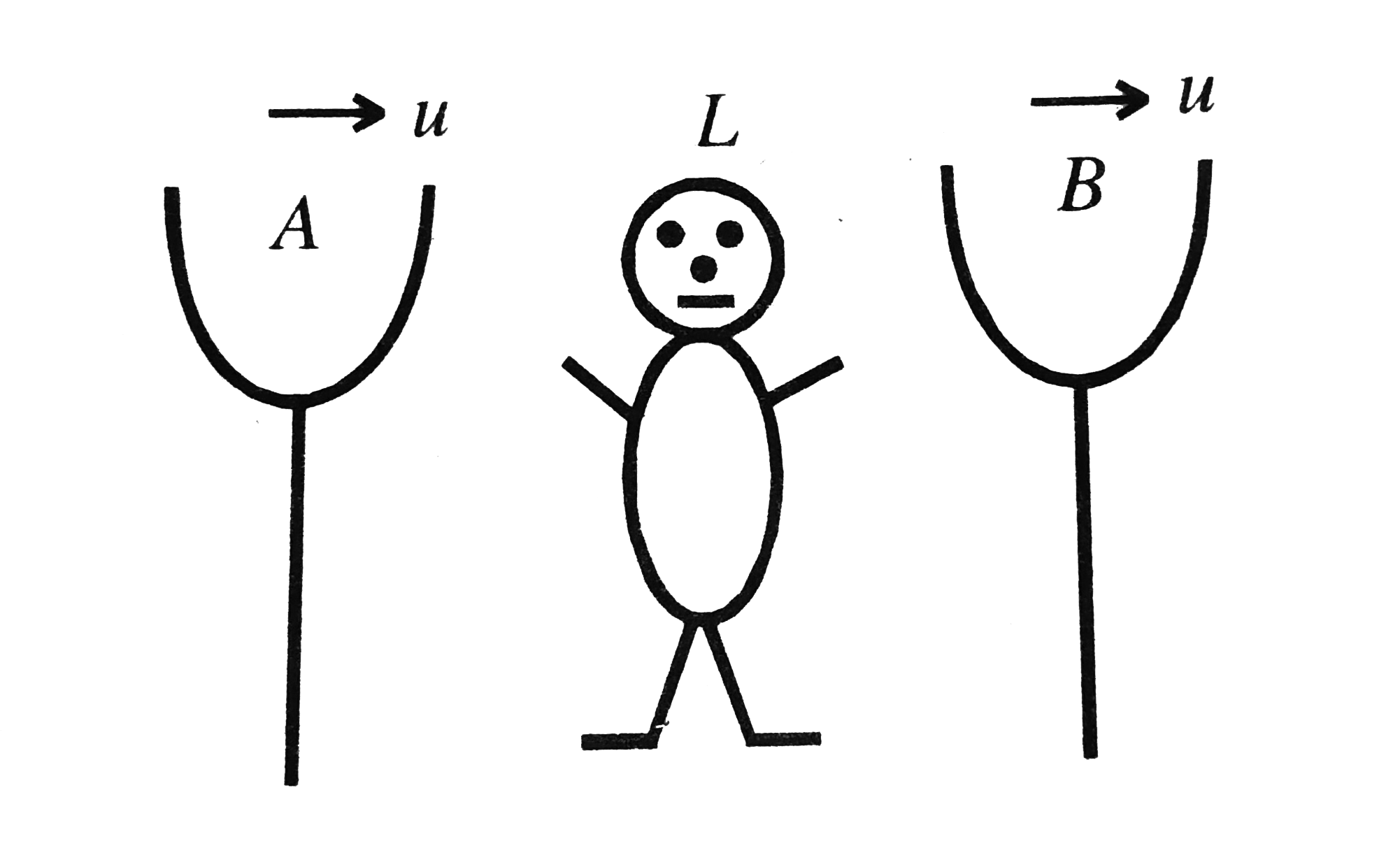 Two tuning forks A and B are vibrating at the same frequency 256 Hz. A listener is standing midway between the forks. If both tuning forks move to the right with a velocity of 5ms, find the number of beats heard per second by the listerner (speed of sound in air is 330ms).
Two tuning forks A and B are vibrating at the same frequency 256 Hz. A listener is standing midway between the forks. If both tuning forks move to the right with a velocity of 5ms, find the number of beats heard per second by the listerner (speed of sound in air is 330ms).
View Solution
As shown if Fig. a vibrating tuning fork of frequency 512 Hz is moving towards the wall with a speed 2ms. Take speed of sound as v=340ms and answer the following questions.
Q. Suppose that a listener is located at rest between the tuning fork and the wall. Number of beats heard by the listener per second will be
View Solution