When a small ice crystal is placed in overcooled water it begins to freeze instantaneously.
i. What amount of ice is formed from 1 kg of water over cooled to −8∘C ? L of water =336×103J/kg and s of water=4200J/kg/K.
ii. What should be the temperature of the overcooled water in order that all of it be converted into ice at 0∘C ?
To solve the problem step by step, we will address both parts of the question.
Part i: Amount of Ice Formed from 1 kg of Water Overcooled to -8°C
1. Identify the given data:
- Mass of water (m) = 1 kg
- Specific heat of water (C) = 4200 J/(kg·K)
- Latent heat of fusion of ice (L) = 336 × 10^3 J/kg
- Initial temperature of water (T_initial) = -8°C
- Final temperature of water (T_final) = 0°C
2. Calculate the heat lost by the overcooled water:
The heat lost (Q_lost) by the water when it warms up from -8°C to 0°C can be calculated using the formula:
Qlost=m⋅C⋅ΔT
where ΔT=Tfinal−Tinitial=0−(−8)=8 K.
Substituting the values:
Qlost=1kg⋅4200J/(kg⋅K)⋅8K=33600J
3. Calculate the mass of ice formed:
The heat gained by the ice (Q_gained) when it freezes can be expressed as:
Qgained=mice⋅L
Setting the heat lost equal to the heat gained:
Qlost=Qgained
33600J=mice⋅(336×103J/kg)
Rearranging to find mice:
mice=33600J336×103J/kg=0.1kg
Part ii: Temperature of Overcooled Water for Complete Freezing
1. Identify the conditions for complete freezing:
We want to find the temperature (T) of the overcooled water such that all of it (1 kg) is converted into ice at 0°C.
2. Set up the heat lost by the overcooled water:
The heat lost by the water can be expressed as:
Qlost=m⋅C⋅(T−0)
where m=1kg and C=4200J/(kg⋅K).
3. Set up the heat gained by the ice:
The heat gained by the ice when it freezes is:
Qgained=mice⋅L=1kg⋅(336×103J/kg)
4. Equate heat lost and heat gained:
Setting the two equations equal:
4200⋅(T−0)=336×103
5. Solve for T:
4200T=336×103
T=336×1034200=−80°C
Final Answers:
- i. The amount of ice formed is 0.1 kg.
- ii. The temperature of the overcooled water should be -80°C for all of it to be converted into ice at 0°C.
- Mass of water (m) = 1 kg
- Specific heat of water (C) = 4200 J/(kg·K)
- Latent heat of fusion of ice (L) = 336 × 10^3 J/kg
- Initial temperature of water (T_initial) = -8°C
- Final temperature of water (T_final) = 0°C
The heat lost (Q_lost) by the water when it warms up from -8°C to 0°C can be calculated using the formula:
Qlost=m⋅C⋅ΔT
where ΔT=Tfinal−Tinitial=0−(−8)=8 K.
Qlost=1kg⋅4200J/(kg⋅K)⋅8K=33600J
The heat gained by the ice (Q_gained) when it freezes can be expressed as:
Qgained=mice⋅L
Setting the heat lost equal to the heat gained:
Qlost=Qgained
33600J=mice⋅(336×103J/kg)
mice=33600J336×103J/kg=0.1kg
We want to find the temperature (T) of the overcooled water such that all of it (1 kg) is converted into ice at 0°C.
The heat lost by the water can be expressed as:
Qlost=m⋅C⋅(T−0)
where m=1kg and C=4200J/(kg⋅K).
The heat gained by the ice when it freezes is:
Qgained=mice⋅L=1kg⋅(336×103J/kg)
Setting the two equations equal:
4200⋅(T−0)=336×103
4200T=336×103
T=336×1034200=−80°C
- i. The amount of ice formed is 0.1 kg.
- ii. The temperature of the overcooled water should be -80°C for all of it to be converted into ice at 0°C.
Topper's Solved these Questions
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Exercise 1.2
22 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Exercise 1.3
18 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Video
Similar Questions
Find the result of mixing 0.5 kg ice at 0∘C with 2 kg water at 30∘C. Given that latent heat of ice is L=3.36×105J/kg and specific heat of water is 4200J/kg/K.
View SolutionA calorimeter of heat capacity 100J/K is at room temperature of 30∘C. 100g of water at 40∘C of specific heat 4200J/kg−K is poured into the calorimeter. What is the temperature of water is calorimeter?
View SolutionAn ice cube of mass 0.1 kg at 0∘C is placed in an isolated container which is at 227∘C. The specific heat s of the container varies with temperature T according to the empirical relation s=A+BT, where A=100cal/kgKandB=2×(10−2)cal/kg. If the final temperature of the container is 27∘C, determine the mass of the container.
(Latent heat of fusion for water = 8×(104)cal/kg, specific heat of water =103cal/kg−K).
View Solution4 kg of ice at −15∘C are added to 5 kg of water at 15∘C . The temperature of the mixture equals
View SolutionWhen a solution w g of urea in 1Kg of water is cooled to −0.372∘C,200gof ice is separated .If Kffor water is 1.86KKgmol−1,w is
View Solution1 kg of ice at 0∘C is mixed with 1.5 kg of water at 45∘C [latent heat of fusion = 80 cal//gl. Then
View SolutionCalculate the amount of heat given out while 400 g of water at 30∘C is
cooled and converted into ice at −2∘C.
Specific heat capacity of water = 4200 J/kg K
Specific heat capacity of ice = 2100 J/ kg K
Specific latent heat of fusion of ice = 33600 J/kg
View Solution
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
Initial mass of the ice in the container equal to
View Solution
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
Initial mass of the ice in the container equal to
View Solution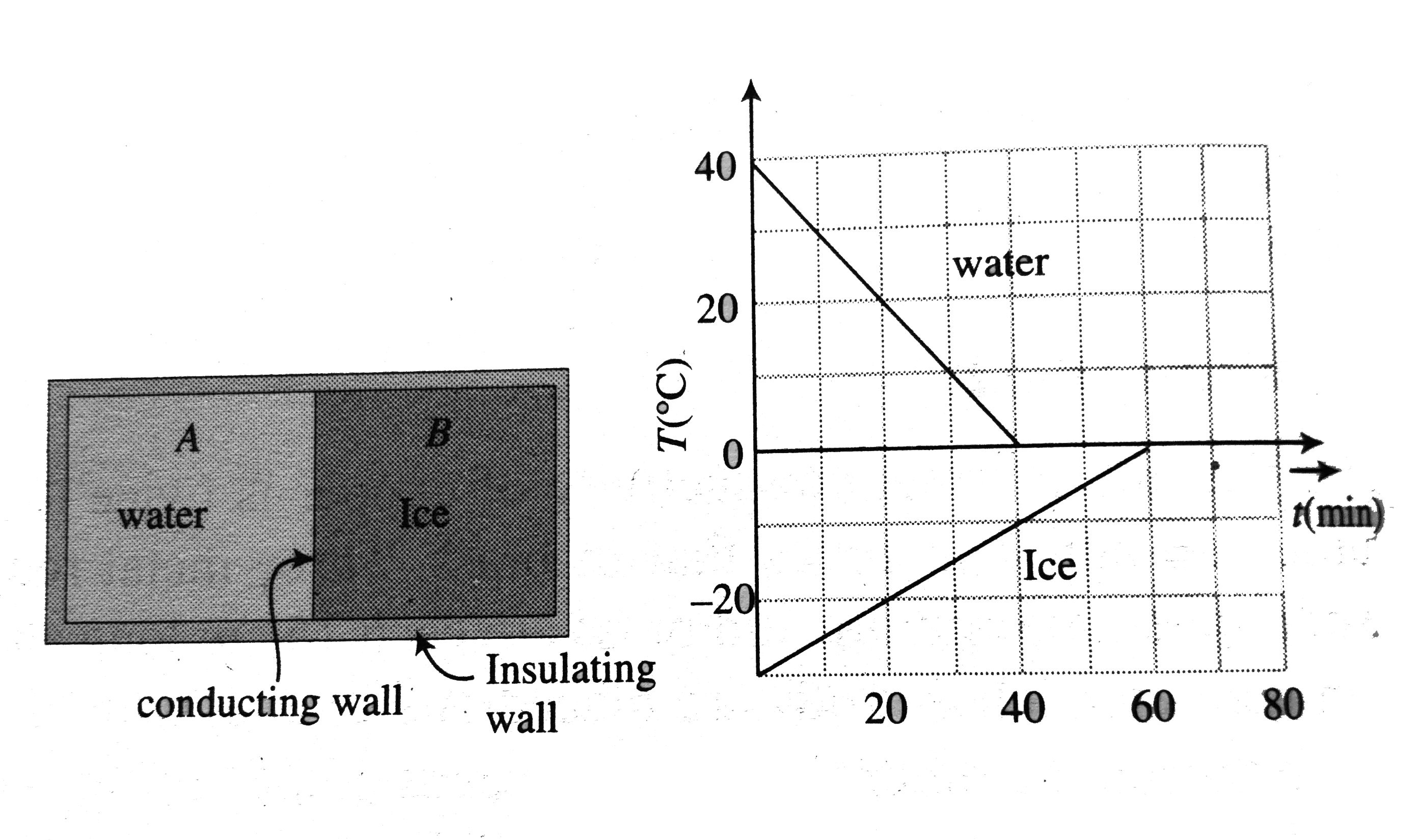
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
The value of rate P is?
View Solution
