An ideal gas (2.0 moles) is carried round a cycle as shown. If the process is isothermal and . Determine
a. work done,
b. change in internal energy,
c. heat supplied to the system during processes , and .
To solve the problem step by step, we need to analyze the processes involved in the cycle of the ideal gas and apply the relevant thermodynamic equations.
Given Data:
- Number of moles (n) = 2.0 moles
- Heat capacity at constant volume (C_V) = 3 cal/mol·K
- Process B to C is isothermal.
Step 1: Work Done (W)
1. Process A to B (Isobaric):
- The work done in an isobaric process is given by:
WAB=PΔV=P(VB−VA)
- Given values: P=4atm, VA=8.2L, VB=16.4L.
- Calculate WAB:
WAB=4atm×(16.4L−8.2L)=4×8.2=32.8L atm
- Convert to Joules (1 L atm = 101.325 J):
WAB=32.8×101.325J=3325.5J
2. Process B to C (Isothermal):
- The work done in an isothermal process is given by:
WBC=nRTln(VCVB)
- Here, R=0.0821L atm/(mol K) and we need to find T using the ideal gas law. Assume T is constant during the process.
- Calculate WBC:
WBC=2.0×4×16.4×101.325×ln(8.216.4)≈−4592.5J
3. Process C to A (Isochoric):
- The work done in an isochoric process is zero:
WCA=0
4. Total Work Done (W):
W=WAB+WBC+WCA=3325.5−4592.5+0=−1267J
Step 2: Change in Internal Energy (ΔU)
1. Process A to B:
- The change in internal energy is given by:
ΔUAB=nCVΔT
- Since CV=3cal/mol K and converting to Joules:
CV=3×4.184=12.552J/mol K
- Calculate ΔUAB:
ΔUAB=2.0×12.552×(TB−TA)
2. Process B to C (Isothermal):
- For isothermal processes, the change in internal energy is zero:
ΔUBC=0
3. Process C to A:
- The change in internal energy is again based on the temperature difference:
ΔUCA=nCV(TA−TC)
4. Total Change in Internal Energy (ΔU):
- The total change in internal energy over a complete cycle is zero:
ΔUtotal=ΔUAB+ΔUBC+ΔUCA=0
Step 3: Heat Supplied to the System (Q)
1. Using First Law of Thermodynamics:
ΔU=Q−W
Rearranging gives:
Q=ΔU+W
2. Calculate Q for each process:
- For process A to B:
QAB=ΔUAB+WAB
- For process B to C:
QBC=ΔUBC+WBC=0−4592.5
- For process C to A:
QCA=ΔUCA+WCA
Final Answers:
- a. Work Done, W=−1267J
- b. Change in Internal Energy, ΔU=0
- c. Heat Supplied, QAB,QBC,QCA can be calculated using the above equations.
- Number of moles (n) = 2.0 moles
- Heat capacity at constant volume (C_V) = 3 cal/mol·K
- Process B to C is isothermal.
- The work done in an isobaric process is given by:
WAB=PΔV=P(VB−VA)
- Given values: P=4atm, VA=8.2L, VB=16.4L.
- Calculate WAB:
WAB=4atm×(16.4L−8.2L)=4×8.2=32.8L atm
- Convert to Joules (1 L atm = 101.325 J):
WAB=32.8×101.325J=3325.5J
- The work done in an isothermal process is given by:
WBC=nRTln(VCVB)
- Here, R=0.0821L atm/(mol K) and we need to find T using the ideal gas law. Assume T is constant during the process.
- Calculate WBC:
WBC=2.0×4×16.4×101.325×ln(8.216.4)≈−4592.5J
- The work done in an isochoric process is zero:
WCA=0
W=WAB+WBC+WCA=3325.5−4592.5+0=−1267J
- The change in internal energy is given by:
ΔUAB=nCVΔT
- Since CV=3cal/mol K and converting to Joules:
CV=3×4.184=12.552J/mol K
- Calculate ΔUAB:
ΔUAB=2.0×12.552×(TB−TA)
- For isothermal processes, the change in internal energy is zero:
ΔUBC=0
- The change in internal energy is again based on the temperature difference:
ΔUCA=nCV(TA−TC)
- The total change in internal energy over a complete cycle is zero:
ΔUtotal=ΔUAB+ΔUBC+ΔUCA=0
ΔU=Q−W
Rearranging gives:
Q=ΔU+W
- For process A to B:
QAB=ΔUAB+WAB
- For process B to C:
QBC=ΔUBC+WBC=0−4592.5
- For process C to A:
QCA=ΔUCA+WCA
- a. Work Done, W=−1267J
- b. Change in Internal Energy, ΔU=0
- c. Heat Supplied, QAB,QBC,QCA can be calculated using the above equations.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Exercise 2.120videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Exercise 2.228videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type14videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
An ideal gas is taken through cycle A→B→C−A, as shown in Fig. IF the net heat supplied to the gas in the cycle is 5 J, the work done by the gas in the process C→A is
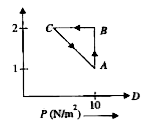 A−5JB−10JC−15JD−20J
A−5JB−10JC−15JD−20J
P-V curve of a diatomic gas is shown in the Fig. Find the total heat given to the gas in the process A→B→C
 View Solution
View SolutionThe enthalpy change for the process
C(graphite)→C(g)is calledView SolutionIf work done by the system is 300 joule when 100 cal. Heat is supplied to it. The change in internal energy during the process is :-
View SolutionChange in internal energy if 20 J heat is supplied to a system has done 50 J work during a thermodynamic process, will be
(a) +30 J
(b) -30 J
(c) +70 J
(d) -70 JView SolutionAn ideal gas is taken through the cycle A→B→C→A, as shown in figure. If the net heat supplied to the gas in the cycle is 5 J the work done by the gas in the process A→B is
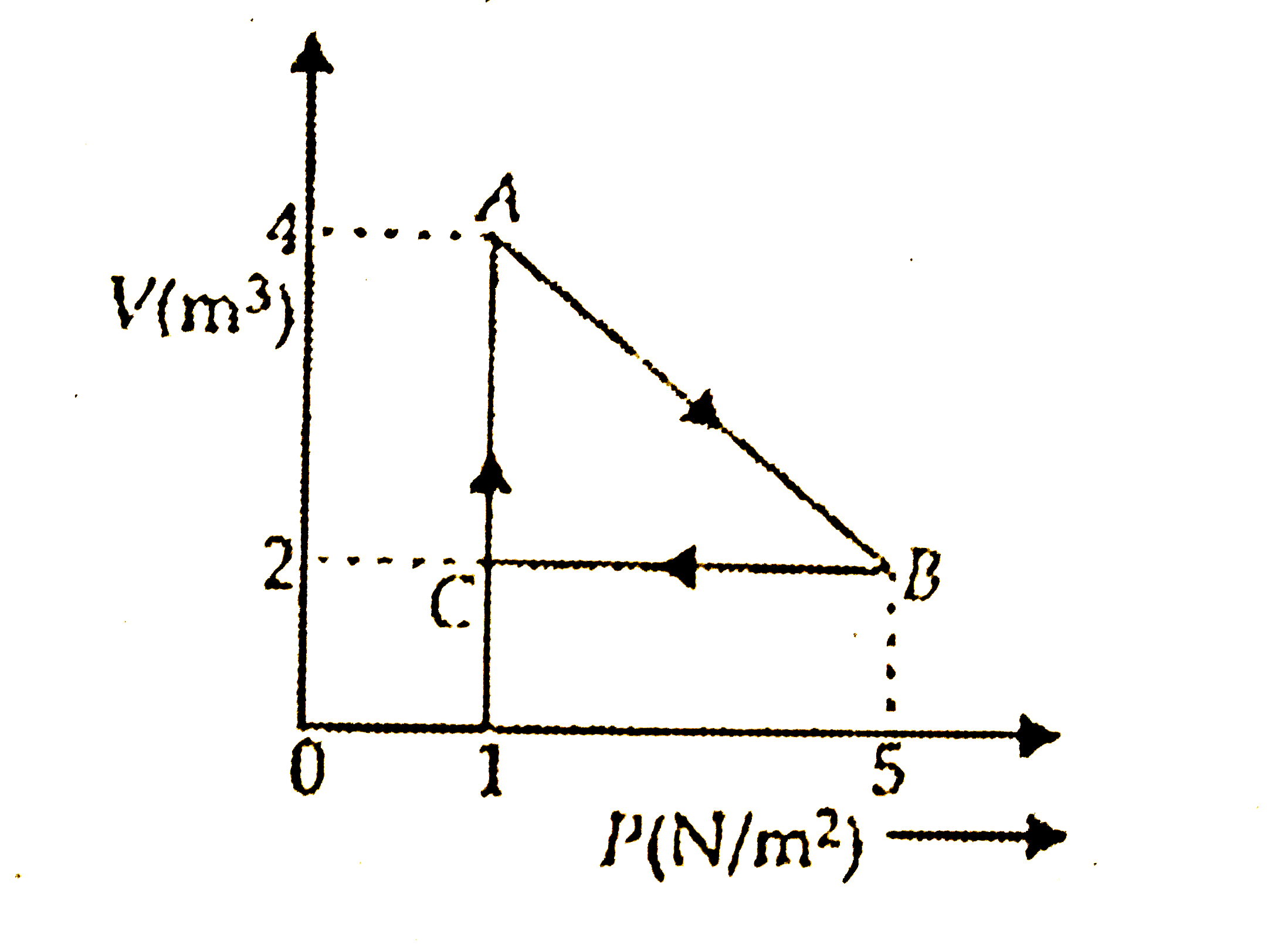 View Solution
View SolutionAn ideal gas (γ=1.67) is taken through the process abc shown in figure . The temperature at the point a is 300k. Calculate (a) the temperature at b and c, (b) the work done in the process, ( c) the amount of heat supplied in the path ab and in the path bc and (d) the change in the internal energy of the gas in the process.
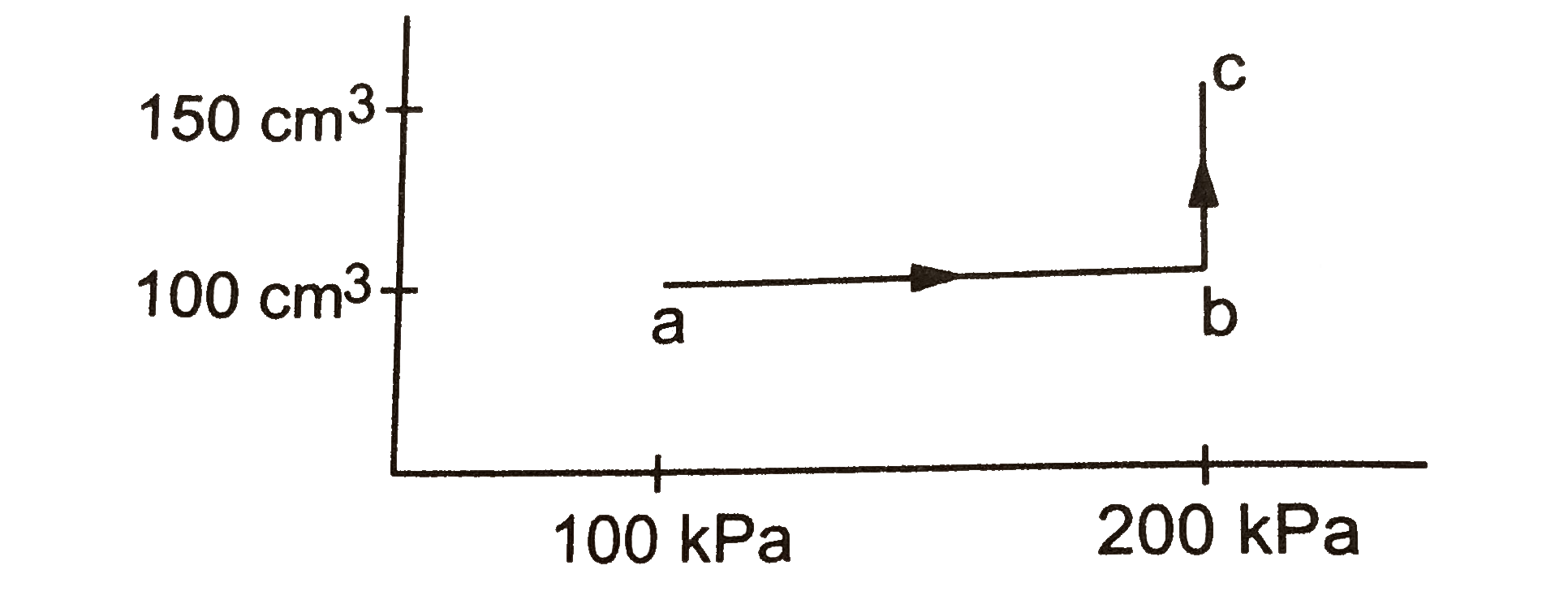 View Solution
View SolutionOne mole of a monatomic gas is taken from a point A to another point B along the path ACB. The initial temperature at A is T0. Calculate the heat abosrbed by the gas in the process A→C→B.
 View Solution
View Solution

