A metal rod AB of length 10x has its one end A in ice at 0∘C, and the other end B in water at 100∘C. If a point P one the rod is maintained at 400∘C, then it is found that equal amounts of water and ice evaporate and melt per unit time. The latent heat of evaporation of water is 540cal/g and latent heat of melting of ice is 80cal/g. If the point P is at a distance of λx from the ice end A, find the value λ. [Neglect any heat loss to the surrounding.]
The correct Answer is:9
To solve the problem, we need to analyze the heat flow through the metal rod and set up equations based on the heat transfer principles. Let's break it down step by step.
Step 1: Understanding the Setup
We have a metal rod AB of length 10x. One end A is at 0∘C (ice) and the other end B is at 100∘C (water). A point P on the rod is maintained at 400∘C. The distance from A to P is λx, and the distance from P to B is 10x−λx.
Step 2: Heat Transfer to Ice
The heat flow from point P to the ice (end A) can be expressed as:
Q1=dm1dt⋅Lf
where Lf is the latent heat of fusion of ice (80 cal/g), and dm1dt is the mass of ice melted per unit time.
Using Fourier's law of heat conduction, we have:
Q1=kA⋅400−0λx=400kAλx
Step 3: Heat Transfer to Water
Similarly, the heat flow from point P to the water (end B) can be expressed as:
Q2=dm2dt⋅Lv
where Lv is the latent heat of vaporization of water (540 cal/g), and dm2dt is the mass of water evaporated per unit time.
Using Fourier's law again, we have:
Q2=kA⋅400−100(10x−λx)=kA⋅300(10−λ)x
Step 4: Setting Up the Equation
Since it is given that equal amounts of water and ice evaporate and melt per unit time, we can set Q1=Q2:
dm1dt⋅Lf=dm2dt⋅Lv
Substituting the expressions for Q1 and Q2:
400kAλx⋅80=300kA(10−λ)x⋅540
Step 5: Simplifying the Equation
We can cancel kA and x from both sides:
400⋅80λ=300⋅54010−λ
Step 6: Cross-Multiplying
Cross-multiplying gives:
400⋅80⋅(10−λ)=300⋅540⋅λ
This simplifies to:
32000(10−λ)=162000λ
Step 7: Expanding and Rearranging
Expanding the left side:
320000−32000λ=162000λ
Rearranging gives:
320000=162000λ+32000λ
320000=194000λ
Step 8: Solving for λ
Now, we can solve for λ:
λ=320000194000≈1.649
Final Answer
Thus, the value of λ is approximately 1.649.
We have a metal rod AB of length 10x. One end A is at 0∘C (ice) and the other end B is at 100∘C (water). A point P on the rod is maintained at 400∘C. The distance from A to P is λx, and the distance from P to B is 10x−λx.
The heat flow from point P to the ice (end A) can be expressed as:
Q1=dm1dt⋅Lf
where Lf is the latent heat of fusion of ice (80 cal/g), and dm1dt is the mass of ice melted per unit time.
Q1=kA⋅400−0λx=400kAλx
Similarly, the heat flow from point P to the water (end B) can be expressed as:
Q2=dm2dt⋅Lv
where Lv is the latent heat of vaporization of water (540 cal/g), and dm2dt is the mass of water evaporated per unit time.
Q2=kA⋅400−100(10x−λx)=kA⋅300(10−λ)x
Since it is given that equal amounts of water and ice evaporate and melt per unit time, we can set Q1=Q2:
dm1dt⋅Lf=dm2dt⋅Lv
Substituting the expressions for Q1 and Q2:
400kAλx⋅80=300kA(10−λ)x⋅540
We can cancel kA and x from both sides:
400⋅80λ=300⋅54010−λ
Cross-multiplying gives:
400⋅80⋅(10−λ)=300⋅540⋅λ
This simplifies to:
32000(10−λ)=162000λ
Expanding the left side:
320000−32000λ=162000λ
Rearranging gives:
320000=162000λ+32000λ
320000=194000λ
Now, we can solve for λ:
λ=320000194000≈1.649
Thus, the value of λ is approximately 1.649.
Topper's Solved these Questions
Similar Questions
A metal rod AB of length 10x has it one end in ice at 0∘C and the other end B in water at 100∘C If a point P on the rod is maintained at 400∘C then it is found that equal amounts of water and ice evaporate and melt per unit time. The latent heat of melting of ice is 80cal/g If the point P is at a distance of λx from the ice end A find the value of λ [neglect any heat loss to the surrounding] .
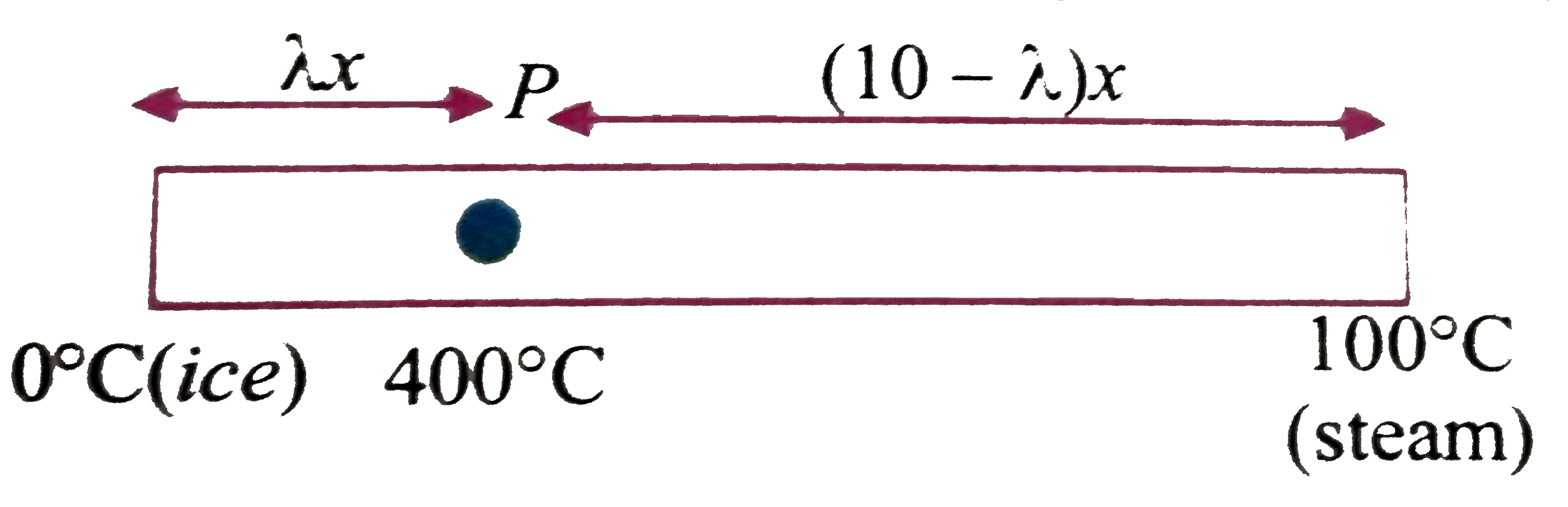 .
.
View SolutionThe latent heat of vaporisation of water is 9700Cal/mole and if the b.p.is 100∘C, ebullioscopic constant of water is
View SolutionOne end of a brass rod of length 2.0 m and cross section 1cm2 is kept in steam at 100∘C and the other end in ice at 0∘C. The lateral surface of the rod is covered by heat insulator. Determine the amount of ice melting per minute. Thermal conductivity of brass is 110W/m−K and specific latent heat of fusion of ice is 80cal/g.
View Solution10 g of ice at 0 C is slowly melted to water at 0 C. The latent heat of melting is 80 cal /g. the change in entropy is ?(cal/k)
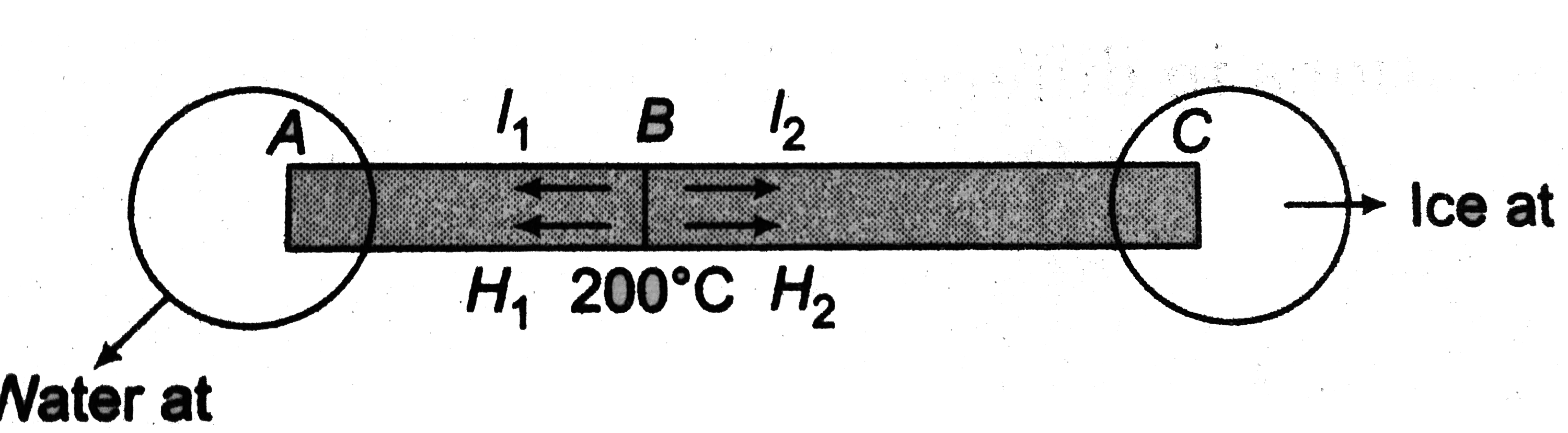
View SolutionB point of the rod shown in figure is maintained at 200∘C. At left end A, there is water at 100∘C and at right end C there is ice at 0∘C. Heat currents H1andH2 will flow on both sides. Due to H1, water will convert into steam and due to H2 ice will be melted. If latent heat of vaporization is 540cal/g and latent heat of fusion is 80cal/g then neglecting the radiation losses find l1l2 so that rate of melting of ice is two times the rate of conversion of water into stream.
 .
.
View SolutionHow should 1 kg of water at 5∘C be divided into two parts so that if one part turned into ice at 0∘C, it would release enough heat to vapourize the other part? Latent heat of steam=540cal/g and latent heat of ice =80cal/g.
View SolutionThe amount of heat required to raise the temperature of 75 kg of ice at 0oC to water at 10oC is (latent heat of fusion of ice is 80 cal/g, specific heat of water is 1 cal/goC)
View Solution1 g of steam at 100∘C and an equal mass of ice at 0∘C are mixed. The temperature of the mixture in steady state will be (latent heat of steam=540cal/g, latent heat of ice =80cal/g,specific heat of water =1cal/g∘C)
View SolutionOne end of a steel rod (K=46Js−1m−1C−1) of length 1.0m is kept in ice at 0∘C and the other end is kept in boiling water at 100∘C . The area of cross section of the rod is 0.04cm2 . Assuming no heat loss to the atmosphere, find the mass of the ice melting per second. Latent heat of fusion of ice =3.36×105Jkg−1 .
View Solution2kg ice at −20∘C is mixed with 5kg water at 20∘C. Then final amount of water in the mixture will be: [specific heat of ice =0.5cal/gm∘C, Specific heat of water =1cal/gm∘C, Latent heat of fusion of ice =80cal/gm]
View Solution
