Given the equetion for a wave on a string
where y and x are in meters and t is in seconds.
(a). At t=0, what are the values of the displacement at x=0,0.1 m,0.2 m, and 0.3m ?
(b). At x=0.1 m what are the values of the displacement at t=0,0.1 s, and 0.2 s?
(c ) what is the equetion for the velocity of oscillation of the particles of the string?
(d). what is the maximum velocity of oscillation?
(e). what is the velocity of propagation of the wave?
(a).
for
similarly for
and for
(b). At
At
(c ). Velocity of particle,
(d). Maximum velocity or the velocity amplitude is
(e). comparing with the wave equation , we have
,and
Therefore,
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Example9videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise 5.19videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct9videos
TRANSMISSION OF HEAT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
The wave described by y =0.25sin(10πx−2πt) where x and y are in meters and t in seconds , is a wave travelling along the
View SolutionA transverse wave travelling on a taut string is represented by:
Y=0.01sin2π(10t−x)
Y and x are in meters and t in seconds. Then,View SolutionThe equation of a progressive wave is
y=0.02sin2π[t0.01−x0.30]
here x and y are in metres and t is in seconds. The velocity of propagation of the wave isView SolutionA travelling wave is given by
y=0.8(3x2+24xt+48t2+4)
where x and y are in metres and t is in seconds. Find the velocity in m/s.View SolutionThe displacement of a string is given by y(x,t)=0.06sin(2πx/3)cos(120πt) where x and y are in m and t in s. The lengthe of the string is 1.5m and its mass is 3.0×10−2kg.
View SolutionThe equation of a travelling wave on a string is y = (0.10 mm )sin[31.4m−1x+(314s−1)t]
View SolutionThe equations for two sinusoidal waves propagating through a string are given by, y1=4sin(20x−30t)
y2=4sin(25−x−40t)
where y and x are in centimeters and t is second.
(i) What is the phase difference between these two waves at the points x=5.0 cm and at t=2.0 s?
(ii) When these two waves interface what is the maximum and minimum value of the intensity?View SolutionVx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?
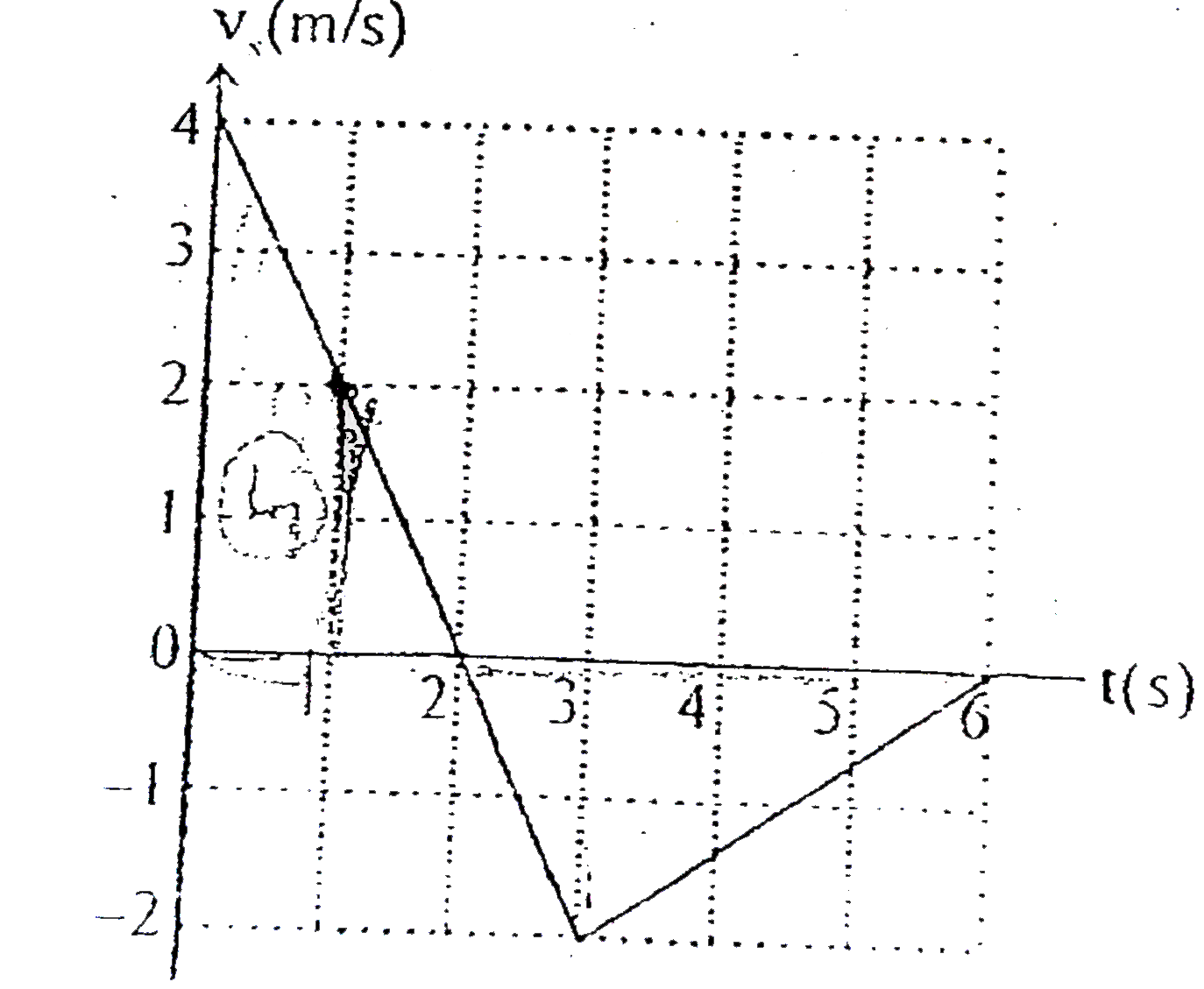 View Solution
View SolutionA wave is represented by the equetion
y=7sin(7πt−0.04πx+π3)
x is in metres and t is in seconds. The speed of the wave isView SolutionA wave is represented by the equetion
y=7sin(7πt−0.04πx+π3)
x is in metres and t is in seconds. The speed of the wave isView Solution

