A transverse wave on a string has an amplitude of 0.2 m and a frequency of 175 Hz. Consider a particle of the string at x=0. it begins with a displacement y=0, at t=0, according to equation y=0.2sin(kx±ωt). How much time passed between the first two instant when this particle has a displacement of y=0.1 m?
1.9 ms
3.9 ms
2.4 ms
0.5 ms
The correct Answer is:a
To solve the problem, we need to find the time interval between the first two instances when a particle of the string has a displacement of y=0.1m. The wave equation is given as:
y=0.2sin(kx−ωt)
Step 1: Set up the equation for displacement
Since we are considering the particle at x=0, the equation simplifies to:
y=0.2sin(−ωt)
We need to find when y=0.1m:
0.1=0.2sin(−ωt)
Step 2: Solve for sine
Dividing both sides by 0.2 gives:
sin(−ωt)=0.10.2=12
Step 3: Find the angles for sine
The sine function equals 12 at:
−ωt=π6and−ωt=5π6
Step 4: Solve for time
From the first equation:
ωt1=−π6⟹t1=−π6ω
From the second equation:
ωt2=−5π6⟹t2=−5π6ω
Step 5: Calculate the time difference
The time difference Δt between the two instances is:
Δt=t2−t1=(−5π6ω)−(−π6ω)
This simplifies to:
Δt=−5π6ω+π6ω=−4π6ω=−2π3ω
Step 6: Substitute for angular frequency
The angular frequency ω is related to the frequency f by the formula:
ω=2πf
Given that the frequency f=175Hz:
ω=2π×175
Substituting ω into the time difference equation:
Δt=−2π3⋅(2π×175)=−23⋅350=−21050=−1525s
Step 7: Convert to milliseconds
To convert seconds to milliseconds:
Δt=−1525×1000≈−1.9ms
Since we are interested in the time interval, we take the absolute value:
Δt≈1.9ms
Final Answer
The time passed between the first two instances when the particle has a displacement of y=0.1m is approximately 1.9 milliseconds.
---
Since we are considering the particle at x=0, the equation simplifies to:
Dividing both sides by 0.2 gives:
The sine function equals 12 at:
From the first equation:
The time difference Δt between the two instances is:
The angular frequency ω is related to the frequency f by the formula:
To convert seconds to milliseconds:
The time passed between the first two instances when the particle has a displacement of y=0.1m is approximately 1.9 milliseconds.
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct Answer
1 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Multiple Correct
25 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Subjective
16 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A certain 120Hz wave on a string has an amplitude of 0.160mm. How much energy exits in an80g length of the string?
View SolutionA transverse wave of amplitude 0.5m and wavelength 1 m and frequency 2 Hz is propagating in a string in the negative x - direction. The expression for this wave is [
View SolutionTransverse waves on a srting have speed 12.0m/s, amplitude 0.05m and wavelength 0.4m. The waves travel in the +x−direction and at t=0 the x=0 end of the string has zero displacement and is moving upwards.
(a) Write a wave function describing the wave.
(b) Find the transverse displacement of a point at x=0.25m at time t=0.15s.
( c ) How much time must elapse from the instant in part (b) until the point at x=0.25m has zero dispacement?
View SolutionFor a certain transverse standing wave on a long string , an antinode is formed at x=0 and next to it , a node is formed at x=0.10m , the displacement y(t)of the string particle at x=0 is shown in Fig.7.97.
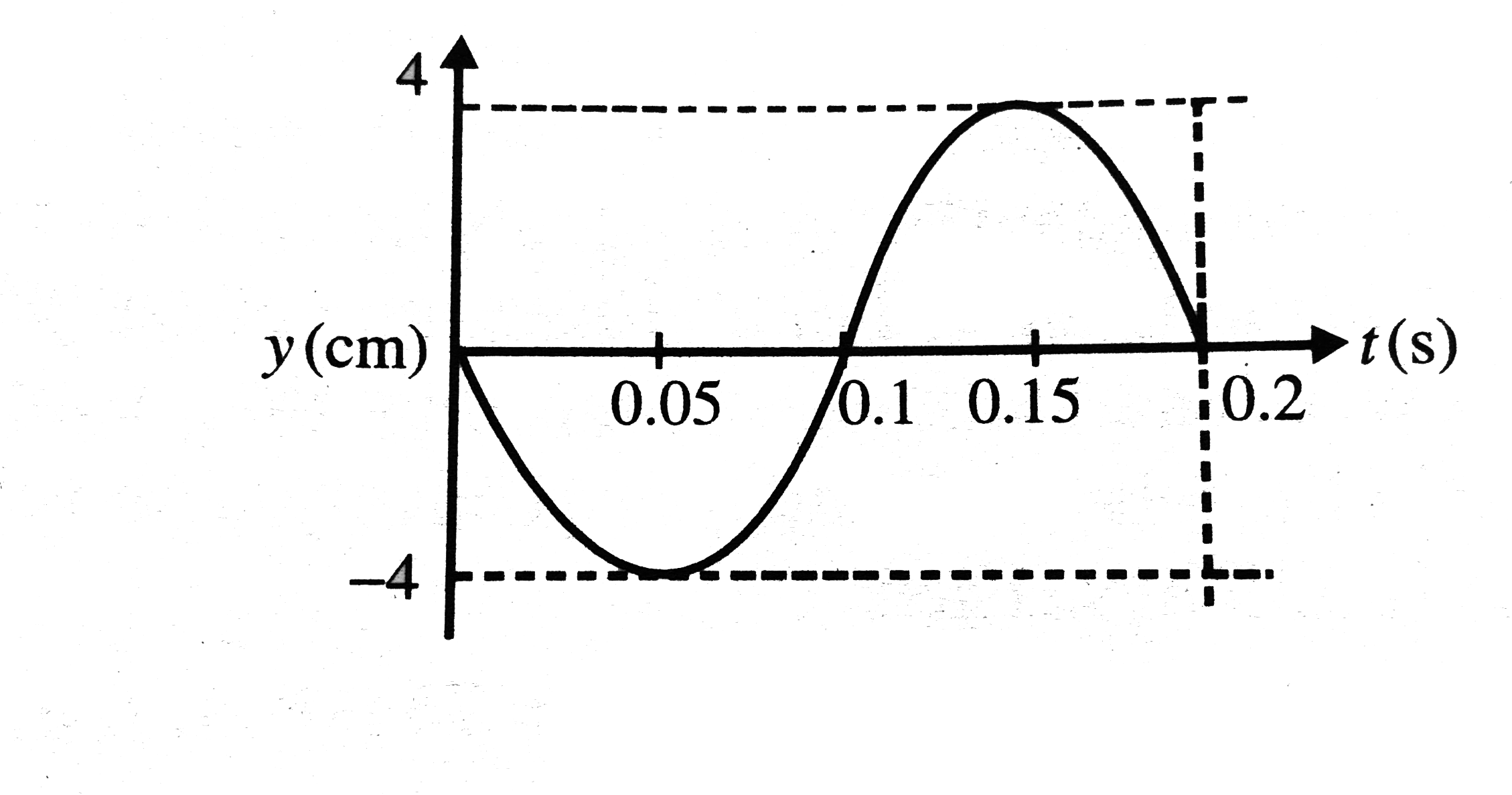
View SolutionFor a certain transverse standing wave on a long string , an antinode is formed at x=0 and next to it , a node is formed at x=0.10m , the displacement y(t)of the string particle at x=0 is shown in Fig.7.97.
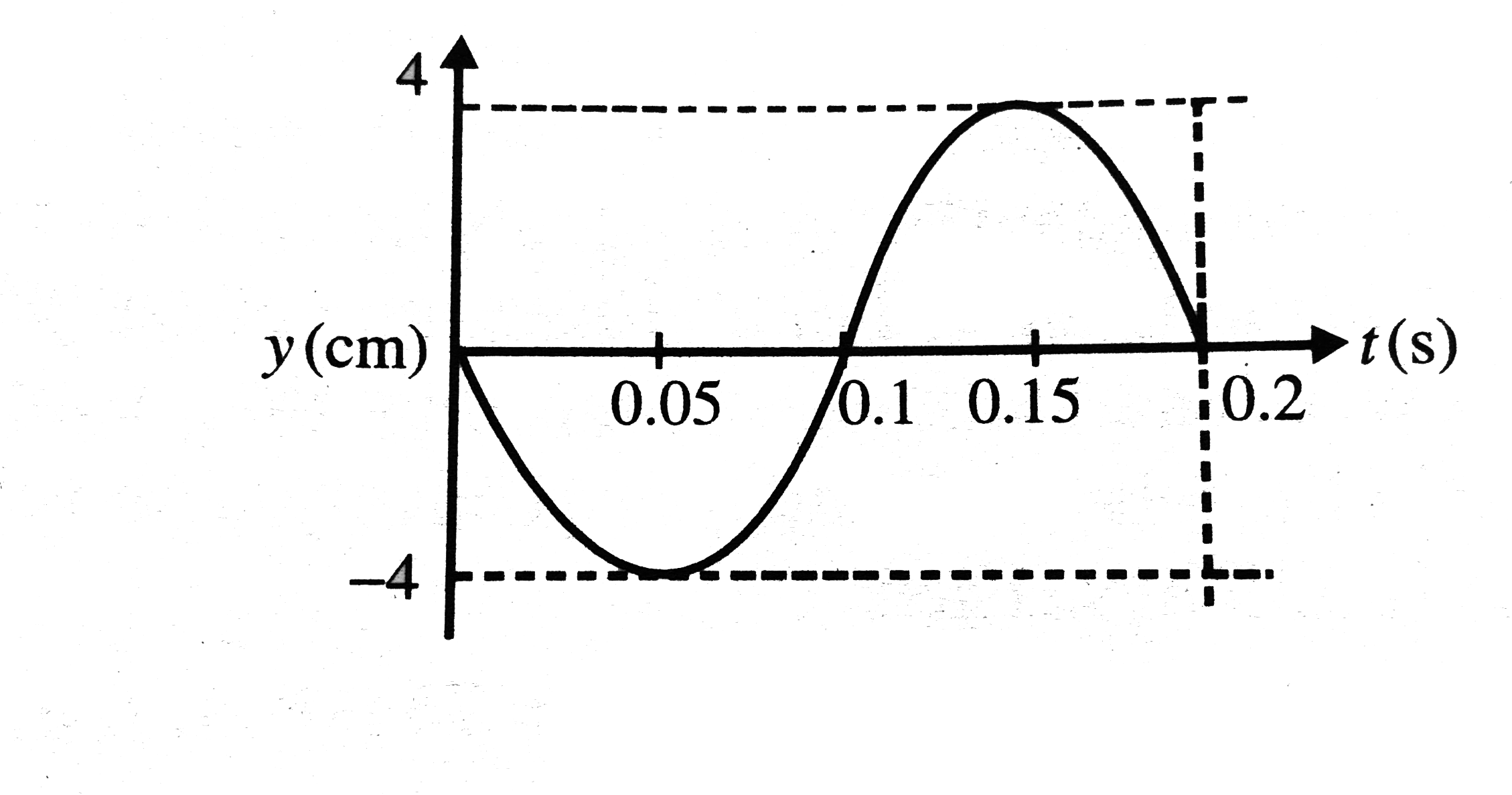
View SolutionA sinusoidal wave is traveling on a string with speed 40 cm/s. The displacement of the particle of the string at x = 10 cm varies with time according to
y = (5.0cm) sin(1.0−4.0s−1)t)The linear density of the string is 4.0 g/cm
View SolutionA transverse wave of amplitude 2 m, wavelength 4 m and frequency 6 Hz is propagating in a string toward positive y-direction. The equation of the wave may be (y is in m and t is in s)
View SolutionA 2 m-long string fixed at both ends is set into vibrations in its first overtone. The wave speed on the string is 200 m s and the amplitude is 0.5 cm. (a) Find the wavelength and the frequency. (b) Write the equation giving the displacement of different points as a function of time. Choose the X-axis along the string with the origin at one end and t = 0 at the instant when the point x= 50 cm has reached its maximum displacement.
View SolutionA particle executing simple harmonic motion has amplitude of 1m and time period 2s. At t=0, net force on the particle is zero. Find the equation of displacement of the particle.
View SolutionTwo particle are executing simple harmonic motion. At an instant of time t their displacement are y1=acos(ωt) and y2=asin(ωt)
Then the phase difference between y1 and y2 is
View Solution
