In which of the following cases the friction force between A and B is maximum in all cases ,.




The correct Answer is:D
To determine in which case the friction force between A and B is maximum, we will analyze each case step by step.
Given:
- Coefficient of friction between A and B, μ1=0.5
- Coefficient of friction between B and the surface, μ2=0
- Mass of A = 2 kg
- Mass of B = 3 kg
- Gravitational acceleration, g=10m/s2
Case Analysis:
Case A:
1. Calculate Normal Force (N):
N=mass of A×g=2kg×10m/s2=20N
2. Calculate Maximum Frictional Force (F_max):
Fmax=μ1×N=0.5×20N=10N
3. Determine Acceleration (a):
a=Fnettotal mass=10N5kg=2m/s2
4. Apply Newton's Second Law on B:
10N−F=3kg×2m/s2
10−F=6⟹F=4N
Result for Case A: Frictional force = 4 N
---
Case B:
1. Calculate Normal Force (N):
N=mass of A×g×cos(37∘)=2kg×10m/s2×45=16N
2. Calculate Maximum Frictional Force (F_max):
Fmax=μ1×N=0.5×16N=8N
3. Determine Force due to Gravity:
Fgravity=mass of A×g×sin(37∘)=2kg×10m/s2×35=12N
4. Since 12 N > 8 N, the frictional force will be limited to F_max:
F=8N
Result for Case B: Frictional force = 8 N
---
Case C:
1. Calculate Normal Force (N):
N=10N
2. Calculate Maximum Frictional Force (F_max):
Fmax=μ1×N=0.5×10N=5N
3. Determine Force due to Gravity:
F=20N (downward)
4. Since 20 N > 5 N, the frictional force will be limited to F_max:
F=5N
Result for Case C: Frictional force = 5 N
---
Case D:
1. Calculate Normal Force (N):
N=2kg×g=20N
2. Calculate Maximum Frictional Force (F_max):
Fmax=μ1×N=0.5×20N=10N
3. Determine Acceleration (a):
a=10N6kg=53m/s2
4. Apply Newton's Second Law on B:
T−F=3kg×53⟹F=5N
Result for Case D: Frictional force = 103N≈3.33N
---
Conclusion:
The maximum frictional force occurs in Case B, where the frictional force is 8 N.
- Coefficient of friction between A and B, μ1=0.5
- Coefficient of friction between B and the surface, μ2=0
- Mass of A = 2 kg
- Mass of B = 3 kg
- Gravitational acceleration, g=10m/s2
1. Calculate Normal Force (N):
N=mass of A×g=2kg×10m/s2=20N
Fmax=μ1×N=0.5×20N=10N
a=Fnettotal mass=10N5kg=2m/s2
10N−F=3kg×2m/s2
10−F=6⟹F=4N
1. Calculate Normal Force (N):
N=mass of A×g×cos(37∘)=2kg×10m/s2×45=16N
Fmax=μ1×N=0.5×16N=8N
Fgravity=mass of A×g×sin(37∘)=2kg×10m/s2×35=12N
F=8N
1. Calculate Normal Force (N):
N=10N
Fmax=μ1×N=0.5×10N=5N
F=20N (downward)
F=5N
1. Calculate Normal Force (N):
N=2kg×g=20N
Fmax=μ1×N=0.5×20N=10N
a=10N6kg=53m/s2
T−F=3kg×53⟹F=5N
The maximum frictional force occurs in Case B, where the frictional force is 8 N.
Similar Questions
For which of the following molecules μ≠0

View SolutionWhich of the following is/are nonpolar (μ=0) ?
View SolutionFor which of the following molecule significant μ≠0 ?
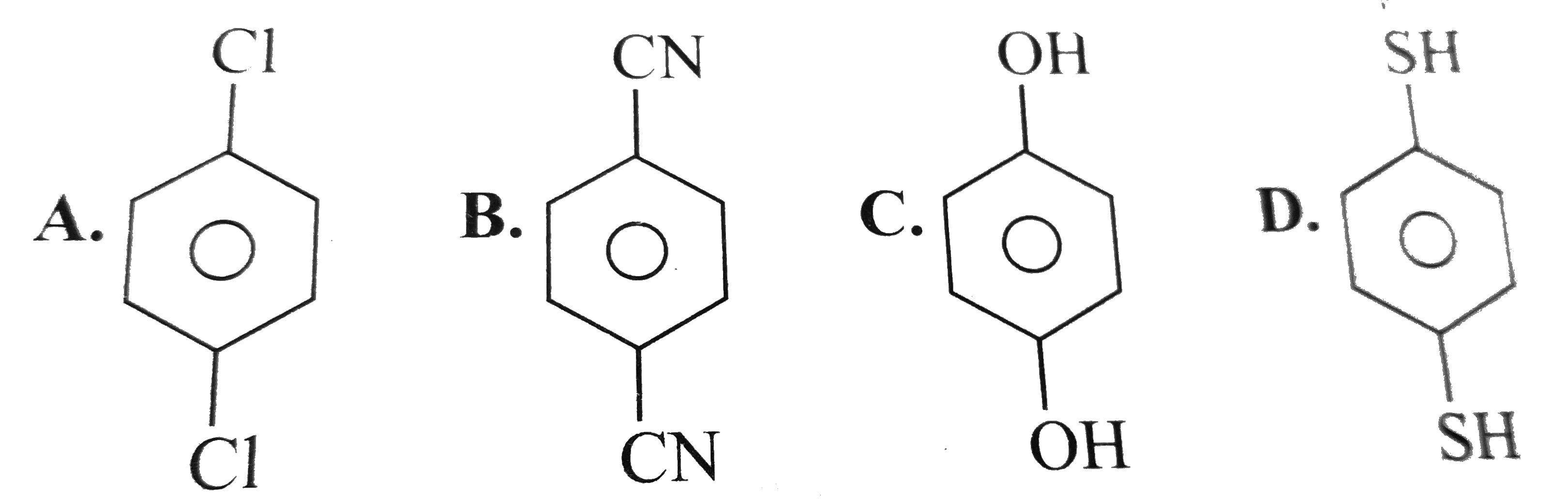
View SolutionFor which of the following molecule significant μ≠0 ?

View SolutionFor which of the following molecule significant μ≠0?

View SolutionIn the figure shown, the wedge is fixedand the masses are released from rest. The coefficient of friction between A and the incline is μ1 and B and the incline is μ2. Then which of the following sentence is (are) correct
(I) normal reaction between A and B can never be zero
(II) normal reaction between A and B is zero only if μ1=μ2

View Solution
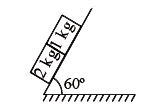
In the figure shown if friction co-efficient of block 1 and 2 with inclined plane is μ1=0.5 and μ2=0.4 respectively, then find out the correct statement.
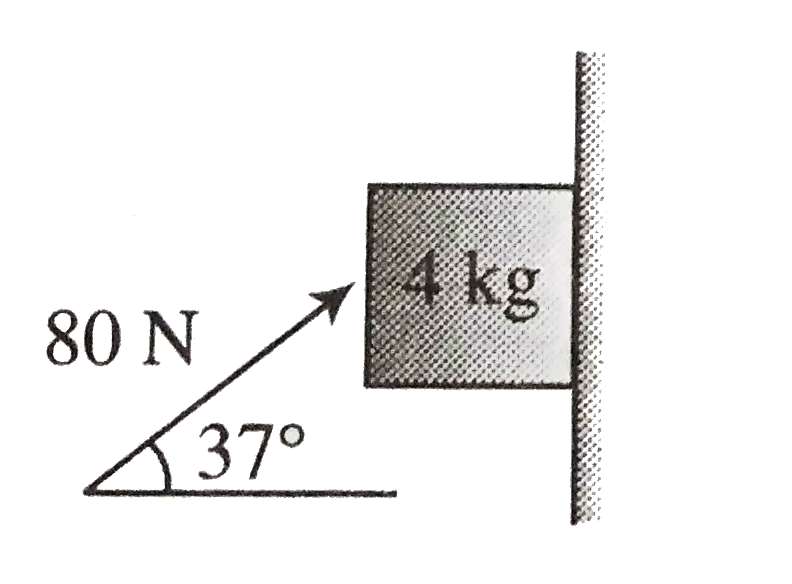
View SolutionA block of mass 4kg is pressed againest the wall by a force of 80N as shown in figure Determine the value of the friction force and block's acceleration (Take μs=0.2,μs=0.15)
View SolutionIn the figure shown, if friction coefficient of block 1 kg and 2kg with inclined plane is μ1=0.5 and μ2=0.4 respectively, then
View SolutionBlock of mass m are released from rest and they slide down the inclined surface as shown in figure. Show that the work done by the frictional forces on the blocks are same in all the cases. Also calculate the speeds with which the blocks reach point B. The coefficient of friction for all the surface is μk.

View Solution
