A particle of mass m is moving with speed u. It is stopped by a force F in distance x if the stopping force is 4 F then
work done by stopping force in second case will be same as that in first case.
work done by stopping force in second case will be 2 times of that in first case.
work done by stopping force in second case will be 12 of that in first case.
work done by stopping force in second case will be 14 of that in first case.
The correct Answer is:A
To solve the problem, we need to analyze the work done by the stopping forces in both cases and relate it to the change in kinetic energy of the particle.
1. Understanding the Initial Conditions:
- A particle of mass m is moving with an initial speed u.
- It is stopped by a force F over a distance x.
2. Calculating Work Done in the First Case:
- The work done W1 by the stopping force F in the first case can be calculated using the formula:
W1=F⋅x
3. Using the Work-Energy Principle:
- According to the work-energy principle, the work done on the particle is equal to the change in kinetic energy:
W=ΔKE=KEfinal−KEinitial
- The initial kinetic energy KEinitial is given by:
KEinitial=12mu2
- Since the particle comes to rest, the final kinetic energy KEfinal is 0. Thus:
W1=0−12mu2=−12mu2
4. Calculating Work Done in the Second Case:
- In the second case, the stopping force is 4F.
- Let x′ be the distance over which the particle is stopped by the force 4F.
- The work done W2 in this case is:
W2=4F⋅x′
5. Applying the Work-Energy Principle Again:
- The change in kinetic energy remains the same since the particle is stopped from the same initial speed u:
W2=−12mu2
6. Equating the Work Done:
- Since both cases result in the same change in kinetic energy, we equate the work done:
4F⋅x′=−12mu2
- From the first case, we know:
F⋅x=−12mu2
- Therefore, we can relate x′ to x:
4F⋅x′=F⋅x⟹x′=x4
7. Conclusion:
- The work done by the stopping force in both cases is equal, as both bring the particle to rest from the same initial speed u.
- Therefore, the correct answer is that the work done by the stopping force in the second case will be the same as that in the first case.
Final Answer:
- The work done by the stopping force in the second case will be the same as that in the first case.
- A particle of mass m is moving with an initial speed u.
- It is stopped by a force F over a distance x.
- The work done W1 by the stopping force F in the first case can be calculated using the formula:
W1=F⋅x
- According to the work-energy principle, the work done on the particle is equal to the change in kinetic energy:
W=ΔKE=KEfinal−KEinitial
- The initial kinetic energy KEinitial is given by:
KEinitial=12mu2
- Since the particle comes to rest, the final kinetic energy KEfinal is 0. Thus:
W1=0−12mu2=−12mu2
- In the second case, the stopping force is 4F.
- Let x′ be the distance over which the particle is stopped by the force 4F.
- The work done W2 in this case is:
W2=4F⋅x′
- The change in kinetic energy remains the same since the particle is stopped from the same initial speed u:
W2=−12mu2
- Since both cases result in the same change in kinetic energy, we equate the work done:
4F⋅x′=−12mu2
- From the first case, we know:
F⋅x=−12mu2
- Therefore, we can relate x′ to x:
4F⋅x′=F⋅x⟹x′=x4
- The work done by the stopping force in both cases is equal, as both bring the particle to rest from the same initial speed u.
- Therefore, the correct answer is that the work done by the stopping force in the second case will be the same as that in the first case.
- The work done by the stopping force in the second case will be the same as that in the first case.
Similar Questions
A particle of mass m initially moving with speed v.A force acts on the particle f=kx where x is the distance travelled by the particle and k is constant. Find the speed of the particle when the work done by the force equals W.
View SolutionTwo bodies of masses 1 kg and 2 kg moving with same velocities are stopped by the same force. Then, the ratio of their stopping distances is
View SolutionA particle of mass M moves with constant speed along a circular path of radius r under the action of a force F. Its speed is
View SolutionA particle of mass 70 g, moving at 50 cm/s , is acted upon by a variable force opposite to its direction of motion. The force F is shown as a function of time t
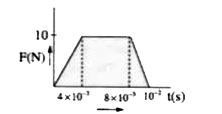
(a) its speed will be 50 cm/s after the force stops acting
(b) its direction of motion will reverse
(c) its average acceleration will be 1m/s2 during the interval in which the force acts
its average acceleration will be 10m/s2 during the interval in which the force acts
View SolutionA particle of mass 1 kg is moving along x - axis and a force F is also acting along x -axis in such a way that its displacement is varying as : x=3t2. Find work done by force F when it will move 2m.
View SolutionA particle of mass m is at rest the origin at time t=0 . It is subjected to a force F(t)=F0e−bt in the x - direction. Its speed v(t) is depicted by which of the following curves ?
View SolutionA particle of mass 0.1 kg is subjected to a force F which varies with distance x as shown. If it starts its journey from rest at x = 0, then its speed at X = 12 m is
View SolutionA car of mass 480 kg moving at a speed of 54 km per hour is stopped in 10 s. Calculate the force applied by the brakes.
View SolutionA particle of mass m moves on the x-axis under the influence of a force of attraction towards the origin O given by F=−kx2ˆi. If the particle starts from rest at x = a. The speed of it will attain to reach at distance x from the origin O will be
View SolutionWhat is the minimum stopping distance for a vehicle of mass m moving with speed v along a level road. If the coefficient of friction between the tyres and the road is μ.
View Solution
