Two object are initially at rest on a frictionless surface. Object 1 has a greater mass than object 2. The same constant force start to act on each object. The force is removed from each object after it accelerates over a distance d. after the force is removed from both objects, which statement is correct (p:momentum, K: kinetic energy)?
p1<p2
p1>p2
K1>K2
K1<K2
The correct Answer is:B
To solve the problem, we need to analyze the motion of two objects (Object 1 and Object 2) subjected to the same constant force over the same distance on a frictionless surface.
1. Define the Masses:
Let the mass of Object 1 be m1 and the mass of Object 2 be m2. We know that m1>m2.
2. Apply Newton's Second Law:
The force F acting on each object can be expressed using Newton's second law:
F=m⋅a
For Object 1:
F=m1⋅a1⟹a1=Fm1
For Object 2:
F=m2⋅a2⟹a2=Fm2
3. Calculate Final Velocity After Distance d:
Using the kinematic equation V2=U2+2aS (where U is the initial velocity, a is acceleration, and S is distance):
Since both objects start from rest, U=0:
For Object 1:
V21=0+2a1d=2(Fm1)d⟹V1=√2Fdm1
For Object 2:
V22=0+2a2d=2(Fm2)d⟹V2=√2Fdm2
4. Calculate Momentum:
Momentum p is given by p=mv.
For Object 1:
p1=m1V1=m1√2Fdm1=√2Fd⋅m1
For Object 2:
p2=m2V2=m2√2Fdm2=√2Fd⋅m2
5. Compare Momentums:
Since m1>m2:
p1=√2Fd⋅m1>√2Fd⋅m2=p2
Thus, p1>p2.
6. Calculate Kinetic Energy:
Kinetic energy K is given by K=12mv2.
For Object 1:
K1=12m1V21=12m1(2Fdm1)=Fd
For Object 2:
K2=12m2V22=12m2(2Fdm2)=Fd
7. Compare Kinetic Energies:
Since both K1 and K2 equal Fd:
K1=K2
Conclusion:
After the force is removed, we conclude that:
- The momentum of Object 1 is greater than the momentum of Object 2 (p1>p2).
- The kinetic energy of both objects is equal (K1=K2).
Final Statements:
- Correct Statement: p1>p2 and K1=K2.
Let the mass of Object 1 be m1 and the mass of Object 2 be m2. We know that m1>m2.
The force F acting on each object can be expressed using Newton's second law:
F=m⋅a
For Object 1:
F=m1⋅a1⟹a1=Fm1
For Object 2:
F=m2⋅a2⟹a2=Fm2
Using the kinematic equation V2=U2+2aS (where U is the initial velocity, a is acceleration, and S is distance):
Since both objects start from rest, U=0:
For Object 1:
V21=0+2a1d=2(Fm1)d⟹V1=√2Fdm1
For Object 2:
V22=0+2a2d=2(Fm2)d⟹V2=√2Fdm2
Momentum p is given by p=mv.
For Object 1:
p1=m1V1=m1√2Fdm1=√2Fd⋅m1
For Object 2:
p2=m2V2=m2√2Fdm2=√2Fd⋅m2
Since m1>m2:
p1=√2Fd⋅m1>√2Fd⋅m2=p2
Thus, p1>p2.
Kinetic energy K is given by K=12mv2.
For Object 1:
K1=12m1V21=12m1(2Fdm1)=Fd
For Object 2:
K2=12m2V22=12m2(2Fdm2)=Fd
Since both K1 and K2 equal Fd:
K1=K2
After the force is removed, we conclude that:
- The momentum of Object 1 is greater than the momentum of Object 2 (p1>p2).
- The kinetic energy of both objects is equal (K1=K2).
- Correct Statement: p1>p2 and K1=K2.
Similar Questions
Two objects are at rest on a level frictionless surface. The objects are not connected. A force F is applied to one of the objects, which then moves with acceleration a. Mark the correct statement(s).
View SolutionForce is applied on an object of mass 2 kg at rest on a frictionless horizontal surface as shown in the graph. The speed of object at t=10 s will be
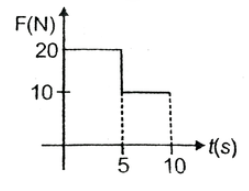
View Solution
Knowledge Check
A force F acting on an object varies with distance x
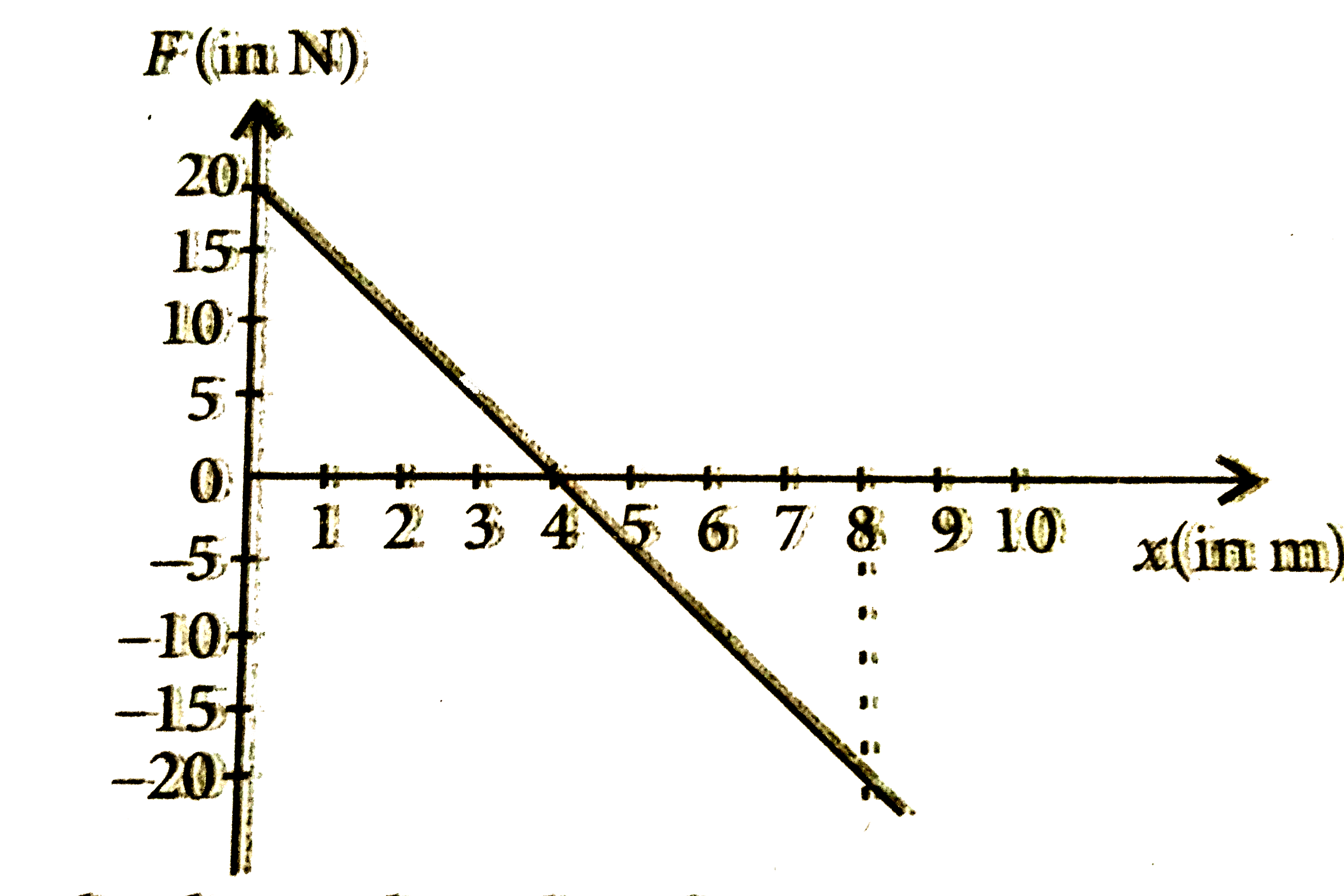
The work done by the force in moving the object from x=0 to x=8 m isAzeroB80 JC−40JD40JTwo objects move toward each other, collide, and separate. If there was not net external force acting on the object, but some kinetic energy was lost, then
Athe collision was elastic and total linear momentum was conservedBthe collision was elastic and total linear mometnum was not conservedCthe collision was not elastic and total linear momentum was conservedDthe collision was not elastic and total linear momentum was not conservedA force F acting on an object varies with distance x as shown in the figure. The work done by the force in moving the object from x=0 to x = 20 m is
 A500 JB1000 JC1500 JD2000 J
A500 JB1000 JC1500 JD2000 J
A force F acting on an object varies with distancex as shown in figure. Work done by the force in moving the object from x = 1 m to x= 6 m is

View SolutionTwo forces of mangitude F1 and F2 are acting on an object.The magnitude of the net force Fnet on the object will be in the range.
View SolutionAn object of mass 10kg moves at a constant speed of 10 ms−1. A constant force, that acts for 4 sec on the object, gives it a speed of 2ms−1 in opposite direction. The force acting on the object is :
View SolutionAn object of mass 2kg is sliding with a constant velocity of 4ms−1 on a frictionless horizontal table. The force required to keep the object moving with the same velocity is
View SolutionThe gravitational force between two object is F. It masses of both object are halved without changing distance between them, then the gravitation force would become
View Solution
