
As shown in figure BEF is a fixed vertical circular tube. A block of mass m starts moving in the tube at point B with velocity V towards E. It is just able to complete the vertical circle. Then.
Velocity at B must be √3Rg
velocity at F must be √2Rg
Normal reaction at point F is 2 mg.
The normal reaction at point E is 6 mg.
Step by step video & image solution for As shown in figure BEF is a fixed vertical circular tube. A block of mass m starts moving in the tube at point B with velocity V towards E. It is just able to complete the vertical circle. Then. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Single Correct Answer type491videos
CENGAGE PHYSICS DPP
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type51videos
CENGAGE PHYSICS DPP
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Comprehension Type31videos
CENGAGE PHYSICS DPP
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer5videos
CAPACITOR AND CAPACITANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Answer Correct Type22videos
COULOMB LAW AND ELECTRIC FIELD
Similar Questions
A particle of mass m attached to an inextensible light string is moving in a vertical circle of radius r. The critical velocity at the highest point is v0 to complete the vertical circle. The tension in the string when it becomes horizontal is
View SolutionA wedge of mass M=2m rests on a smooth horizontal plane. A small block of mass m rests over it at left end A as shown in figure. A sharp impulse is applied on the block, due to which it starts moving to the right with velocity v0=6ms−1. At highest point of its trajectory, the block collides with a particle of same mass m moving vertically downwards with velocity v=2ms−1 and gets stuck with it. If the combined body lands at the end point A of body of mass M, calculate length l. Neglect friction (g=10ms−2).
 View Solution
View SolutionA uniform rod of mass m and length / is hinged at upper end. Rod is free to rotate in vertical plane. A bail of mass m moving horizontally with velocity vo collides at lower end of rod perpendicular to it and sticks to it. The minimum velocity of the ball such that combined system just completes the vertical circle will be
View SolutionA particle of maas m is attched to a light string of length l, the other end of which is fixed. Initially the string is kept horizontal and the particle is given an upwrd velocity v. The particle is just able to complete a circle
View SolutionA small spherical ball is suspended through a string of length l . The whole arrangement is placed in a vehicle which is moving with velocity v . Now, suddenly the vehicle stops and ball starts moving along a circular path. If tension in the string at the highest point is twice the weight of the ball then (assume that the ball completes the vertical circle)
View SolutionA point mass m is connected with ideal inextensible string of length l and other end of string is tied at point O as shown in the figure. The string is made horizontal and mass is released from point A to perform vertical circular motion. There is a nail at point N such that ON =r . Find the value of r so that mass m is able to just perform complete vertical circular motion about point N.
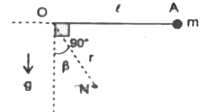 View Solution
View SolutionA small ball of mass m is released in a smooth circular tube as shown in figure. The minimum height h such that bead can complete the circle is
View SolutionA particle is given an intial speed u inside a smooth spherical shell of radius R so that it is just able to complete the circle. Acceleration of the particle, when its velocity is vertical, is
 View Solution
View SolutionA block A of mass 2m is hanging from a vertical massless spring of spring constant k and is in equilibrium. Another block B of mass m strikes the block A with velocity u and sticks to it as shown in the figure. The magnitude of the acceleration of the combined system of the blocks just after the collision is
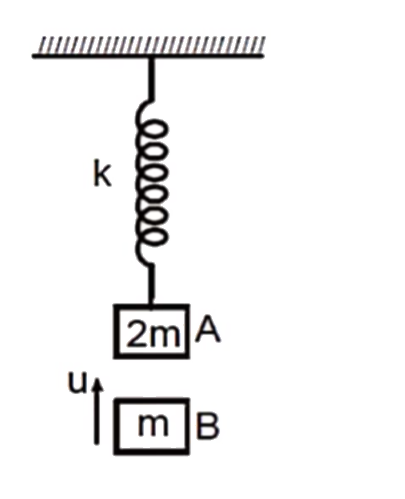 View Solution
View SolutionA spring of mass m lies on a smooth table. One, end of it is clamped to the vertical wall and other end is attached to a mass m ( as shown in fig) and is placed on a horizontal frictionless surface. If the block of mass M is given a velocity v0 towards right find the K.E. of the system . ( AsSigmae velocity in spring is varying linearly).
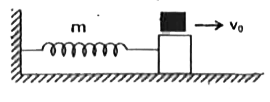 View Solution
View Solution
