When two point charges qA and qB are placed at some separation on positive x-axis at points (xA,0) and (xB,0). Given that |qA| and |qB| and xB>xA. If null point is the point where net electric field due to both the charges is zero, then
if both qA and qB are positive, null point lies at some point xA<x<xB
if qA is positive and qB is negative, null point lies at some point x<xA
if qA is positive and qB is negative, null point lies at some point x>xB
if qA is negative and qB is positive, null point lies at some point x>xB
The correct Answer is:A, C, D
To solve the problem of finding the null point where the net electric field due to two point charges qA and qB is zero, we can follow these steps:
Step 1: Understand the Configuration
We have two point charges:
- Charge qA is located at position (xA,0)
- Charge qB is located at position (xB,0)
- It is given that |qA|>|qB| and xB>xA.
Step 2: Determine the Regions for Electric Field
The electric field due to a positive charge points away from the charge, while the electric field due to a negative charge points towards the charge. We can analyze the electric field in three regions:
1. To the left of qA (Region 1)
2. Between qA and qB (Region 2)
3. To the right of qB (Region 3)
Step 3: Analyze Electric Field Directions
1. Region 1 (Left of qA):
- Both electric fields due to qA and qB point to the right (away from both charges if they are positive).
- The net electric field cannot be zero here.
2. Region 2 (Between qA and qB):
- The electric field due to qA points to the right (away from qA).
- The electric field due to qB points to the left (away from qB).
- Since |qA|>|qB|, the electric field due to qA will dominate. Therefore, the net electric field cannot be zero here.
3. Region 3 (Right of qB):
- The electric field due to qA points to the right.
- The electric field due to qB also points to the right.
- The net electric field cannot be zero here either.
Step 4: Identify the Null Point
Since the null point must be located where the electric fields from both charges are equal in magnitude and opposite in direction, we conclude that:
- The null point must lie in Region 2, between qA and qB, closer to the smaller charge qB.
Step 5: Conclusion
Thus, the null point lies between xA and xB, specifically closer to qB.
Summary of Findings
- The null point exists between the two charges.
- It is closer to the charge with the smaller magnitude, which is qB.
We have two point charges:
- Charge qA is located at position (xA,0)
- Charge qB is located at position (xB,0)
- It is given that |qA|>|qB| and xB>xA.
The electric field due to a positive charge points away from the charge, while the electric field due to a negative charge points towards the charge. We can analyze the electric field in three regions:
1. To the left of qA (Region 1)
2. Between qA and qB (Region 2)
3. To the right of qB (Region 3)
1. Region 1 (Left of qA):
- Both electric fields due to qA and qB point to the right (away from both charges if they are positive).
- The net electric field cannot be zero here.
- The electric field due to qA points to the right (away from qA).
- The electric field due to qB points to the left (away from qB).
- Since |qA|>|qB|, the electric field due to qA will dominate. Therefore, the net electric field cannot be zero here.
- The electric field due to qA points to the right.
- The electric field due to qB also points to the right.
- The net electric field cannot be zero here either.
Since the null point must be located where the electric fields from both charges are equal in magnitude and opposite in direction, we conclude that:
- The null point must lie in Region 2, between qA and qB, closer to the smaller charge qB.
Thus, the null point lies between xA and xB, specifically closer to qB.
- The null point exists between the two charges.
- It is closer to the charge with the smaller magnitude, which is qB.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Answer Correct Type
22 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Correct Answer Type
24 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
Two point charges Q and -Q/4 are separated by a distance x.

View Solution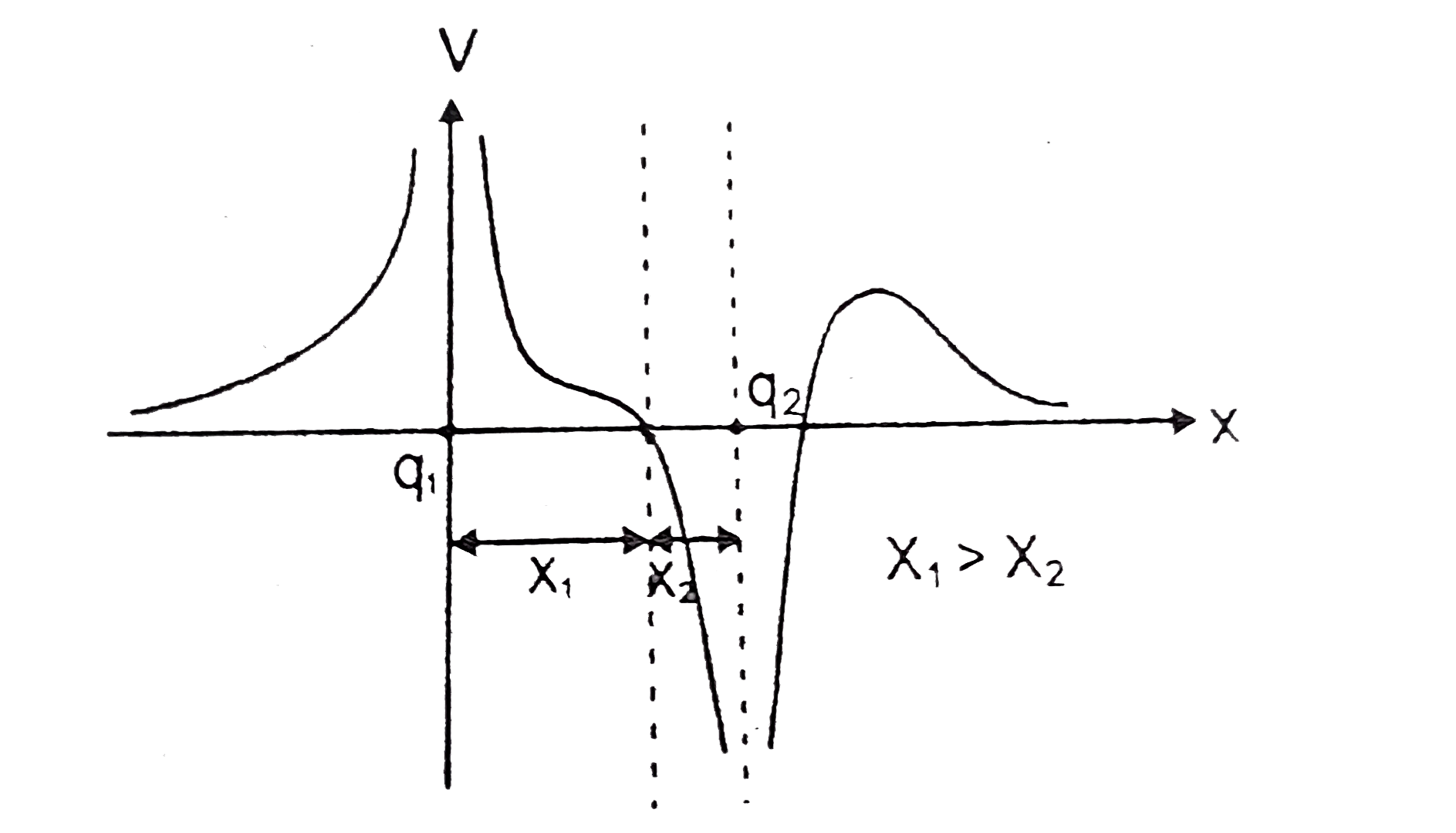
Two point charges (q1 and q2) are placed on x-axis, figure shows graph potential (V) on x-axis. With x-co-ordinate:
View SolutionTwo point charges +4q and +q are placed 30cm apart. At what point on the line joining them is the electric field zero
View Solutiontwo point charges + 16 q and -4q located at x=0 and x=L respectively. the location of a point on the x-axis from x=0, at which the net electric field due to these two charges is zero is
View SolutionTwo point charges +8q and −2q are located at x=0 and x=L respectively. The location of a point on the x axis at which the net electric field due to these two point charges is zero is
View SolutionThe positions of two point charges q1 and q2 are →r1 and →r2 , respectively. Find the position of the point where the net field is zero due to thses charges.
View SolutionPoint charges +4q,−q and +4q are kept on the x-axis at points x=0,x=a and x=2a respectively, then
View SolutionTwo point charges +8q and -2q are located at x=0 and x=L respectively. The location of a point on the x-axis from +8q at which the net electric field due to these two point charges is zero is
View SolutionTwo point charges −q and +q are located at points (0,0−a) and (0,0,a) respectively. The electric potential at point (0,0,z)is (Z>a)
View SolutionTwo charges q1andq2 are placed at (0,0,d) and (0,0,-d) respectively. Find locus of points where the potential is zero.
View Solution
