A negative charge Q is distributed uniformly in volume of a sphere is radius R and a point charge particle (may be negative or positive) is present on the surface of this sphere then variation of escape velocity (vs) of charge 'q' as a function of 'q' will be [negect gravitational interaction].
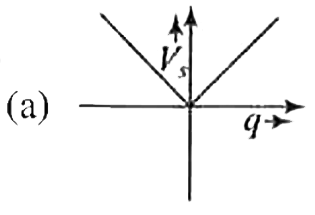
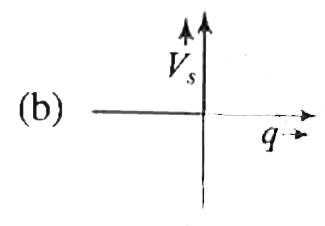
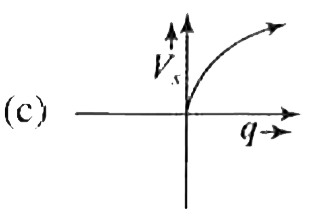

The correct Answer is:C
To solve the problem, we need to analyze the escape velocity of a charge q placed on the surface of a uniformly charged sphere with a negative charge Q distributed throughout its volume.
1. Understanding Escape Velocity:
The escape velocity vs is the minimum velocity required for an object to escape the gravitational or electrostatic influence of another object. In this case, we are dealing with electrostatic forces since we are neglecting gravitational interactions.
2. Energy Conservation Principle:
The total mechanical energy at the point of escape must equal zero. The kinetic energy of the charge q when it is at the surface of the sphere is given by:
KE=12mv2s
where m is the mass of the charge q and vs is the escape velocity.
3. Electrostatic Potential Energy:
The electrostatic potential energy U at the surface of the sphere due to the charge Q is given by:
U=kQqR
where k is Coulomb's constant, Q is the charge distributed in the sphere, q is the charge at the surface, and R is the radius of the sphere.
4. Setting Up the Equation:
According to the conservation of energy:
12mv2s+kQqR=0
Rearranging gives:
12mv2s=−kQqR
5. Solving for Escape Velocity:
Now, we can express vs:
v2s=−2kQqmR
Taking the square root:
vs=√−2kQqmR
6. Analyzing the Sign of Q:
- If Q is negative, then −Q is positive, and since q can be either positive or negative, we need to analyze both cases:
- If q is positive, vs will be real and positive.
- If q is negative, vs will be zero because the product Qq will be positive, leading to a zero escape velocity.
7. Conclusion:
The escape velocity vs is proportional to the square root of |q| when Q is negative and q is positive. Therefore, we can conclude that:
- For Q<0 and q>0, vs is proportional to √q.
- For Q<0 and q<0, vs=0.
Final Result:
The variation of escape velocity vs as a function of charge q is:
- vs∝√|q| for q>0
- vs=0 for q<0
The escape velocity vs is the minimum velocity required for an object to escape the gravitational or electrostatic influence of another object. In this case, we are dealing with electrostatic forces since we are neglecting gravitational interactions.
The total mechanical energy at the point of escape must equal zero. The kinetic energy of the charge q when it is at the surface of the sphere is given by:
KE=12mv2s
where m is the mass of the charge q and vs is the escape velocity.
The electrostatic potential energy U at the surface of the sphere due to the charge Q is given by:
U=kQqR
where k is Coulomb's constant, Q is the charge distributed in the sphere, q is the charge at the surface, and R is the radius of the sphere.
According to the conservation of energy:
12mv2s+kQqR=0
Rearranging gives:
12mv2s=−kQqR
Now, we can express vs:
v2s=−2kQqmR
Taking the square root:
vs=√−2kQqmR
- If Q is negative, then −Q is positive, and since q can be either positive or negative, we need to analyze both cases:
- If q is positive, vs will be real and positive.
- If q is negative, vs will be zero because the product Qq will be positive, leading to a zero escape velocity.
The escape velocity vs is proportional to the square root of |q| when Q is negative and q is positive. Therefore, we can conclude that:
- For Q<0 and q>0, vs is proportional to √q.
- For Q<0 and q<0, vs=0.
The variation of escape velocity vs as a function of charge q is:
- vs∝√|q| for q>0
- vs=0 for q<0
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.515videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.320videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q2videos
ELECTRICAL MEASURING INSTRUMENTS
Similar Questions
A rubber balloon is given a charge Q distributed uniformly over its surface. Then
View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring.
 View Solution
View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring .The
 View Solution
View SolutionA charge q is distributed uniformly on the surface of a sold sphere of radius R. It covered by a concentric hollow conduction sphere of radius 2R. Find the charges inner and outer surface of hollow sphere if it is earthed.
 View Solution
View SolutionA charge q0 is distributed uniformly on a ring of radius R. A sphere of equal radius R constructed with its centre on the circumference of the ring. Find the electric flux through the surface of the sphere.
View SolutionCharge Q is uniformly distributed throughout the volume of a solid hemisphere of radius R metres. Then the potential at centre O of hemisphere in volts is:
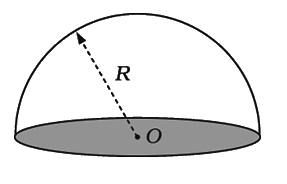 View Solution
View SolutionFlux passing through the shaded surface of a sphere when a point charge q is placed at the center is (radius of the sphere is R)
 View Solution
View SolutionLet P(r)=QπR4r be the charge density distribution for a solid sphere of radius R and total charge Q. For a point 'p' inside the sphere at distance r1 from the centre of the sphere, the magnitude of electric field is:
View SolutionA uniformly charged solid sphere a mass M, radius R having charge Q is rotated about its diameter with frequency f0. The magnetic moment of the sphere is
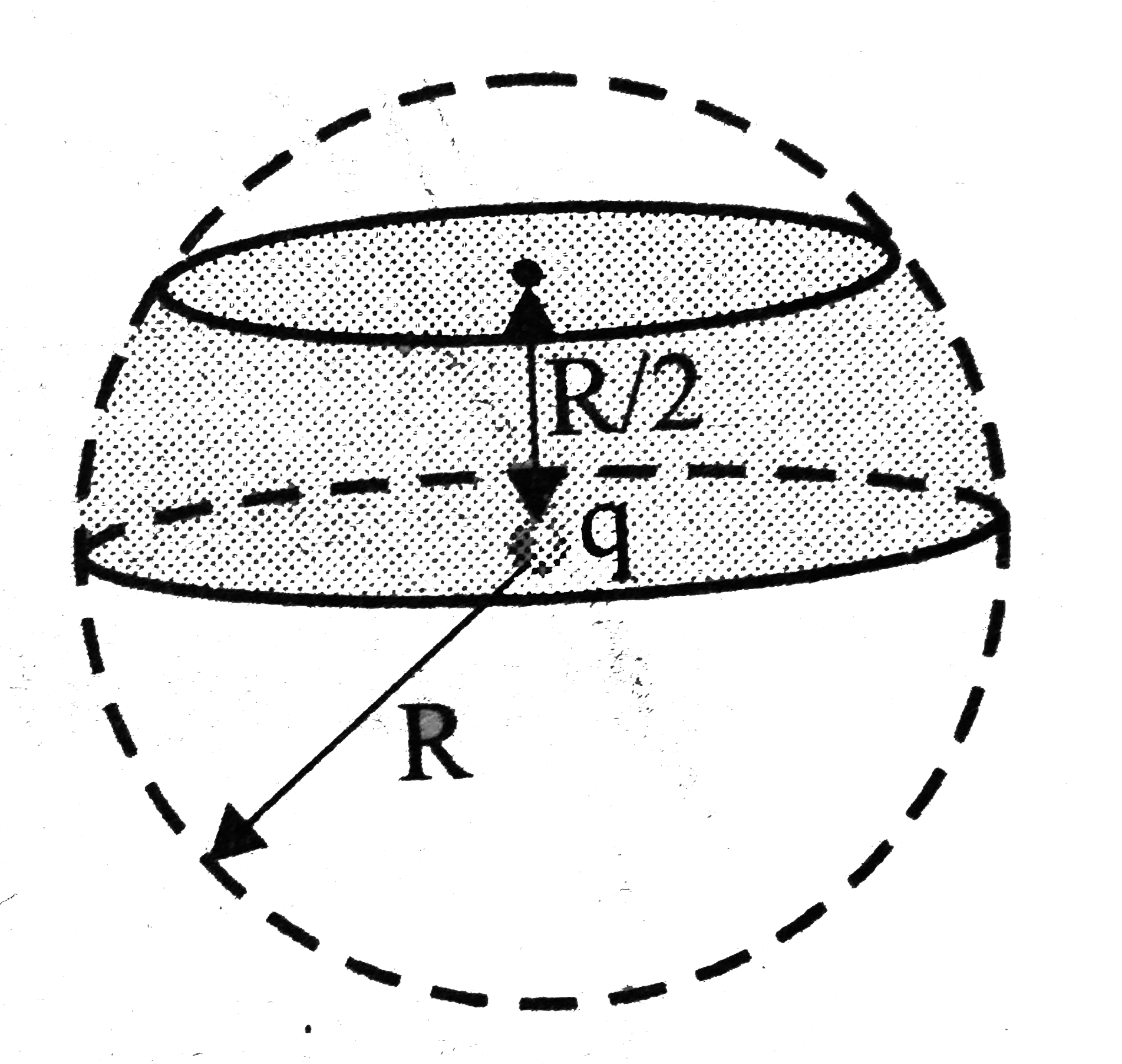
View SolutionA positive charge Q is uniformly distributed throughout the volume of a dielectric sphere of radius R. A point mass having charge +q and mass m is fired toward the center of the sphere with velocity v from a point at distance r(r>R) from the center of the sphere. Find the minimum velocity v so that it can penetrate (R/2) distance of the sphere. Neglect any resistance other than electric interaction. Charge on the small mass remains constant throughout the motion.
 View Solution
View Solution

