A glass tube 1.5m long and open at both ends, is immersed vertically in a water tank completely. A tuning fork of 660 Hz is vibrated and kept at the upper end of the tube and the tube is gradually raised out of water the total number of resonances heard before the tube comes out of water taking velocity of sound air 330m/s is
12
6
8
4
The correct Answer is:B
To solve the problem, we need to find the total number of resonances heard as the glass tube is raised out of the water. The tube is open at both ends, and we can use the formula for the frequency of a tube open at both ends to find the number of resonances.
1. Identify the Given Values:
- Length of the tube, L=1.5m
- Frequency of the tuning fork, f=660Hz
- Velocity of sound in air, v=330m/s
2. Understand the Resonance Condition:
For a tube open at both ends, the resonance frequencies are given by:
fn=n⋅v2L
where n is the harmonic number (1, 2, 3,...).
3. Rearranging the Formula:
We can rearrange the formula to solve for n:
n=2Lfv
4. Substituting the Values:
Now, substitute the known values into the equation:
n=2⋅1.5m⋅660Hz330m/s
5. Calculating the Value of n:
- Calculate the numerator:
2⋅1.5⋅660=1980
- Now divide by the velocity:
n=1980330=6
6. Conclusion:
The total number of resonances heard before the tube comes out of the water is n=6.
Final Answer:
The total number of resonances heard is 6.
---
- Length of the tube, L=1.5m
- Frequency of the tuning fork, f=660Hz
- Velocity of sound in air, v=330m/s
For a tube open at both ends, the resonance frequencies are given by:
fn=n⋅v2L
where n is the harmonic number (1, 2, 3,...).
We can rearrange the formula to solve for n:
n=2Lfv
Now, substitute the known values into the equation:
n=2⋅1.5m⋅660Hz330m/s
- Calculate the numerator:
2⋅1.5⋅660=1980
- Now divide by the velocity:
n=1980330=6
The total number of resonances heard before the tube comes out of the water is n=6.
The total number of resonances heard is 6.
Topper's Solved these Questions
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Multiple Correct Answers Type
5 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Fill in the Blanks Type
34 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Integer
9 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 24
1 Videos
Similar Questions
A glass tube of 1.0m length is filled with water . The water can be drained out slowly at the bottom of the tube . A vibrating tuning fork of frequency 500Hz is brought at the upper end of the tube and the velocity of sound is 330m/s. Find the number of resonances that can be obtained.
View SolutionA glass tube of 1.0m length is filled with water . The water can be drained out slowly at the bottom of the tube . If a vibrating tuning fork of frequency 500c/s is brought at the upper end of the tube and the velocity of sound is 330m/s, then the total number of resonances obtained will be
View Solution
Knowledge Check
A glass tube of 1.0m length is filled with water . The water can be drained out slowly at the bottom of the tube . If a vibrating tuning fork of frequency 500Hz is brought at the upper end of the tube and the velocity of sound is 300m/s, then the total number of resonances obtained will be
AA. 4BB. 3CC. 2D4. 1A long glass tube is held vertically in water . A tuning fork is struck and held over the tube . Strong resonances are observed at two successive lengths 0.50mand0.84m above the surface of water . If the velocity of sound is 340m/s, then the frequency of the tuning fork is
A128 HzB256 HzC384 HzD500 Hz
A tuning fork of frequency 340Hz is excited and held above a cylindrical tube of length 120cm. It is slowly filled with water. The minimum height of water column required for resonance to be first heard( Velocity of sound =340ms−1) is.
View SolutionA tuning fork of frequency 340Hz is excited and held above a cylindrical tube of length 120cm. It is slowly filled with water. The minimum height of water column required for resonance to be first heard( Velocity of sound =340ms−1) is.
View SolutionThe water level in a vertical glass tube 1.0m long can be adjusted to any position in the tube . A tuning fork vibrating at 660HZ is held just over the open top end of the tube . At what positions of the water level wil they be in resonance? Speed of sound is 330m/s .
View SolutionWater rises to a height h in a capillary tube lowered vertically into water to a depth l as shown in the figure. The lower end of the tube is now closed, the tube is the taken out of the water and opened again. The length of the water column remaining in the tube will be
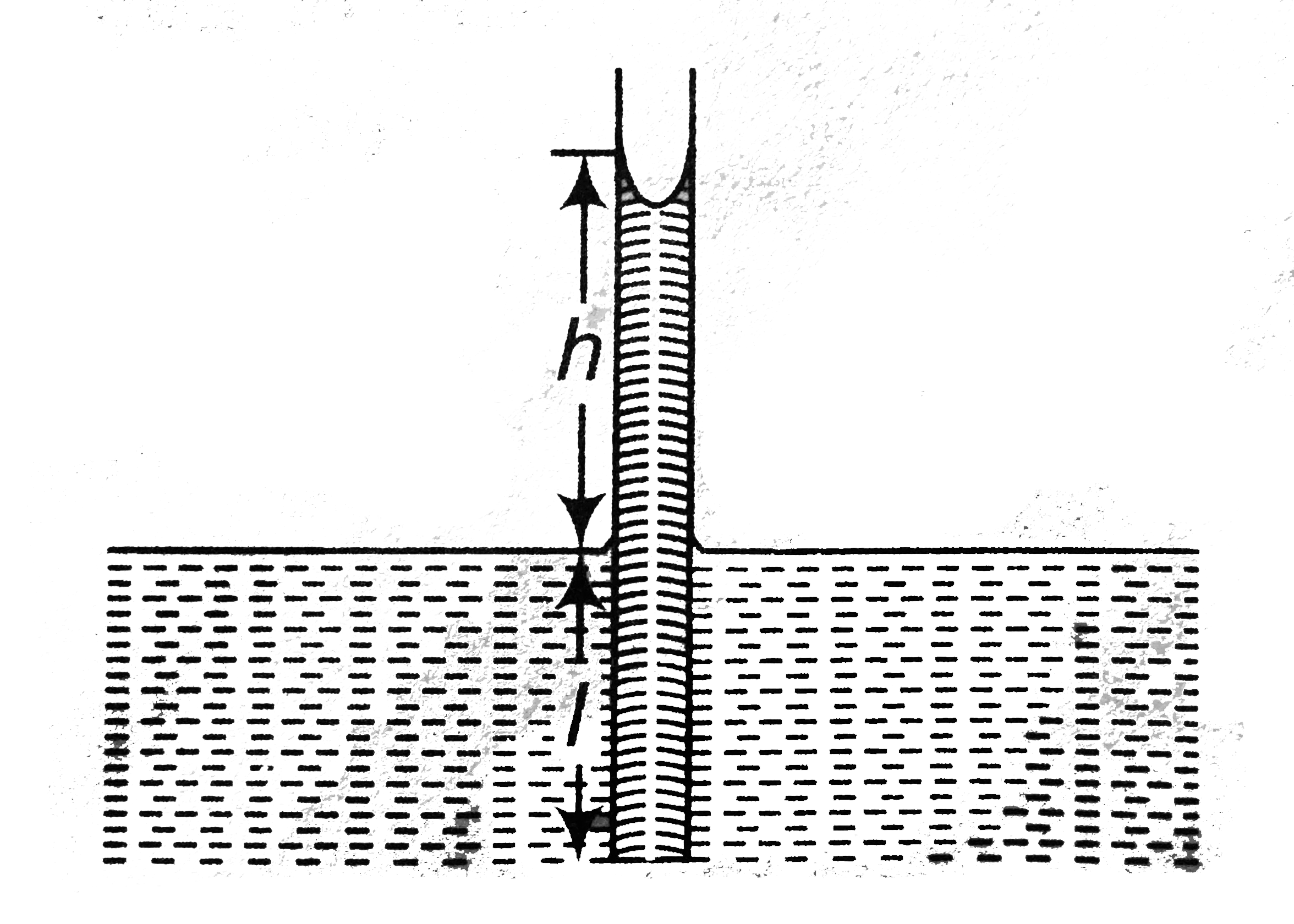 .
.
View SolutionA loudspeaker that produces signals from 50 to 500Hz is placed at the open end of a closed tube of length 1.1m. The lowest and the highest frequency that excites resonance in the tube are f1andfh respectively . The velocity of sound is 330m/s. Then
View SolutionA stationary wave is set up in a resonance air column of a glass tube partially filled with water by holding a tuning fork near the open end, the open end of the tube is :
View Solution
