A cane is taken out from a refrigerator at 0∘C. The atmospheric temperature is 25∘C. If t1 is the time taken to heat from 0∘C to 5∘C and t2 is the time taken from 10∘C to 15∘C, then the wrong statements are
(1) t1>t2
(2)t1=t2
(3) There is no relation
(4)t1<t2
t1>t2
t1<t2
t1=t2
There is no relation
To solve the problem, we will analyze the heating of the cane using Newton's Law of Cooling. The law states that the rate of change of temperature of an object is proportional to the difference between its temperature and the surrounding temperature.
1. Identify the Initial Conditions:
- The cane is taken out from a refrigerator at 0∘C.
- The surrounding atmospheric temperature is 25∘C.
2. Calculate the Average Temperature for the First Interval:
- For the first interval, we are heating the cane from 0∘C to 5∘C.
- The average temperature Tavg1 during this interval is:
Tavg1=0+52=2.5∘C
3. Apply Newton's Law of Cooling for the First Interval:
- The rate of change of temperature can be expressed as:
dTdt=K(Tavg1−Tsurrounding)
- Substituting the values:
dTdt=K(2.5−25)=K×(−22.5)
- This indicates that the temperature change is negative, meaning the cane is gaining heat from the surroundings.
4. Calculate the Average Temperature for the Second Interval:
- For the second interval, we are heating the cane from 10∘C to 15∘C.
- The average temperature Tavg2 during this interval is:
Tavg2=10+152=12.5∘C
5. Apply Newton's Law of Cooling for the Second Interval:
- The rate of change of temperature can be expressed as:
dTdt=K(Tavg2−Tsurrounding)
- Substituting the values:
dTdt=K(12.5−25)=K×(−12.5)
6. Determine the Time Taken for Each Interval:
- The time taken t1 to heat from 0∘C to 5∘C and t2 to heat from 10∘C to 15∘C can be compared using the rates of temperature change.
- Since the temperature change dT is the same (5 degrees) for both intervals, we can set up the ratio:
t2t1=22.512.5
- Simplifying this gives:
t2t1=22.512.5=1.8
- Thus, t2>t1.
7. Conclusion:
- From the analysis, we find that t2 is greater than t1, which means the statement t1<t2 is correct.
- Therefore, the wrong statements are:
- (1) t1>t2
- (2) t1=t2
- (3) There is no relation
- The correct statement is (4) t1<t2.
- The cane is taken out from a refrigerator at 0∘C.
- The surrounding atmospheric temperature is 25∘C.
- For the first interval, we are heating the cane from 0∘C to 5∘C.
- The average temperature Tavg1 during this interval is:
Tavg1=0+52=2.5∘C
- The rate of change of temperature can be expressed as:
dTdt=K(Tavg1−Tsurrounding)
- Substituting the values:
dTdt=K(2.5−25)=K×(−22.5)
- This indicates that the temperature change is negative, meaning the cane is gaining heat from the surroundings.
- For the second interval, we are heating the cane from 10∘C to 15∘C.
- The average temperature Tavg2 during this interval is:
Tavg2=10+152=12.5∘C
- The rate of change of temperature can be expressed as:
dTdt=K(Tavg2−Tsurrounding)
- Substituting the values:
dTdt=K(12.5−25)=K×(−12.5)
- The time taken t1 to heat from 0∘C to 5∘C and t2 to heat from 10∘C to 15∘C can be compared using the rates of temperature change.
- Since the temperature change dT is the same (5 degrees) for both intervals, we can set up the ratio:
t2t1=22.512.5
- Simplifying this gives:
t2t1=22.512.5=1.8
- Thus, t2>t1.
- From the analysis, we find that t2 is greater than t1, which means the statement t1<t2 is correct.
- Therefore, the wrong statements are:
- (1) t1>t2
- (2) t1=t2
- (3) There is no relation
- The correct statement is (4) t1<t2.
Topper's Solved these Questions
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Fill in the blacks type
6 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 24
1 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Integer
9 Videos
Similar Questions
A body takes T minutes to cool from 62∘C to 61∘C when the surrounding temperature is 30∘C. The time taken by the body to cool from 46∘C to 45.5∘C is
View SolutionA particle executes SHM in accordance with x=Asinωt. If t1 is the time taken by it to reach from x=0 to x=√3(A/2)and t2 is the time taken by it to reach from x=√3/2A to x=A , the value of t1/t2 is
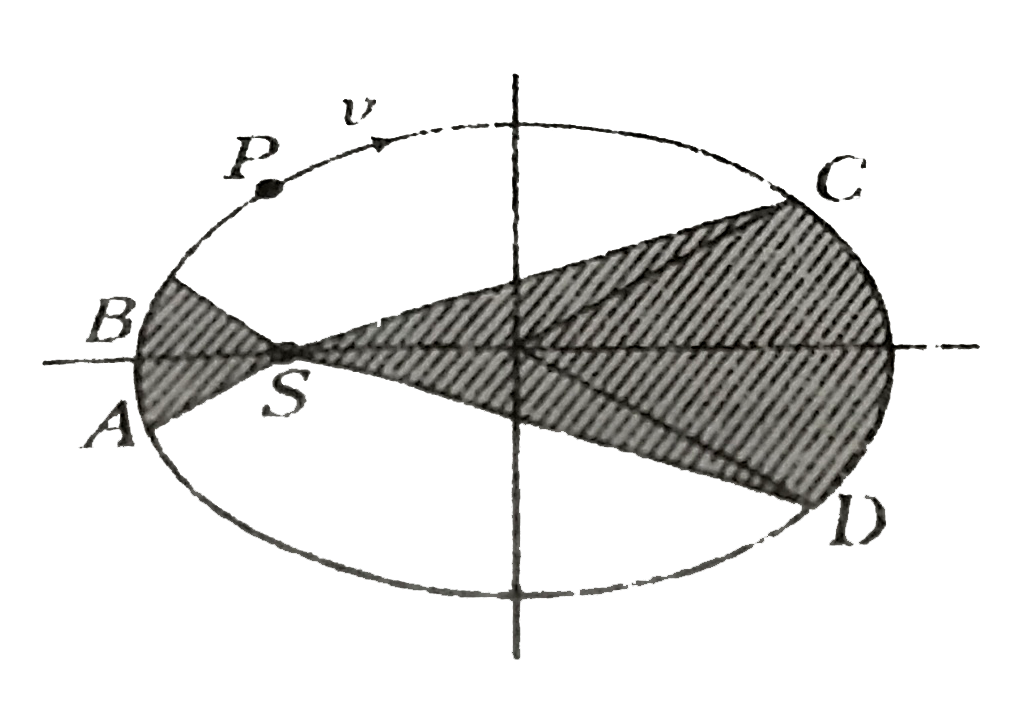
View SolutionThe figure shows elliptical orbit of a plant P about the sun S. The shaded area CSD is twice tha shaded area ASB. If t1 is the time taken by the planet to move from C to D and t2 is the time to move from A to B, determine the ratio t1/t2
View SolutionA bucket full of hot water cools from 75∘C to 70∘C in time T1, from 70∘C to 65∘C in time T2 and from 65∘C to 60∘C in time T3, then
View SolutionA tank full of water has a small hole at its bottom. Let t1 be the time taken to empty first one third of the tank and t2 be the time taken to empty second one third of the tank and t3 be the time taken to empty rest of the tank then
(a). t1=t2=t3
(b). t1>t2>t3
(c). t1<t2<t3
(d). t1>t2<t3
View SolutionA substance cools from 75∘C to70∘C in T1 minute, from 70∘C to 65∘C in T2 minute and from 65∘C→60∘C in T3 minute, then.
View SolutionFind the time taken by the particle in going from x = (A)/2) to x=A Hint :Timetaken→goomx=0→x =A Time taken to go from x=0→x= (A)/(2)Requiredtime= t_(1) - t_(2)
View SolutionA vessel full of hot water is kept in a room and it cools from 80∘C to 75∘C in T1 minutes, from 75∘C to 70∘C in T2 minutes and from 70∘C to 65∘C in T3 minutes Then .
View SolutionIf t1,t2,t3 are the feet of normals drawn from (x1,y1) to the parabola y2=4ax then the value of t1t2t3 =
View SolutionGibbs-Helmoholtz equation relates the free energy change to the enthalpy and entropy changes of the process as
(ΔG)PT=ΔH−TΔS
The magnitude of ΔH does not change much with the change in temperature but the energy factor TΔS changes appreciably. Thus, spontaneity of a process depends very much on temperature.
The dissolution of CaCl2.6H2O in a large volume of water is endothermic to the extent of 3.5kcalmol−1. For the reaction. CaCl2(s)+6H2O(l)→CaCl2.6H2O(s)ΔHis−23.2kcal. The heat of solution of anhydrous CaCI2 in large quantity of water will be
View Solution
