A closed hollow insulated cylinder is filled with gas at 0∘C and also contains an insulated piston of negligible weight and negligible thickness at the middle point. The gas on one side of the piston is heated to 100∘C. If the piston moves 5cm the length of the hollow cylinder is
13.65 cm
27.5 cm
38.6 cm
64.6 cm
The correct Answer is:D
To solve the problem step by step, we will use the principles of the ideal gas law and the concept of thermal expansion due to temperature change.
1. Understanding the Setup:
- We have a closed hollow insulated cylinder divided by a piston.
- One side of the piston contains gas at 0∘C (273 K) and the other side contains gas at 100∘C (373 K).
- The piston moves 5 cm when the gas on one side is heated.
2. Using the Ideal Gas Law:
- The ideal gas law states that PV=nRT, where P is pressure, V is volume, n is the number of moles, R is the gas constant, and T is the temperature in Kelvin.
- Since the cylinder is insulated, the pressure on both sides of the piston remains equal when the piston moves.
3. Setting Up the Equations:
- Let the length of the cylinder be L.
- The volume on the left side (initial) is V1=A⋅L2 (where A is the cross-sectional area).
- The volume on the right side (after the piston moves) is V2=A⋅(L2+5).
4. Applying the Ideal Gas Law:
- For the left side (initial state at 0∘C):
P1⋅A⋅L2=n1⋅R⋅273
- For the right side (final state at 100∘C):
P2⋅A⋅(L2+5)=n2⋅R⋅373
5. Equating Pressures:
- Since the piston is in equilibrium, P1=P2.
- Thus, we can set the equations equal to each other:
P1⋅A⋅L2273=P2⋅A⋅(L2+5)373
6. Canceling Common Terms:
- We can cancel A and P1 from both sides:
L/2273=(L2+5)373
7. Cross-Multiplying:
- Cross-multiplying gives:
373⋅L2=273⋅(L2+5)
8. Expanding and Simplifying:
- Expanding the right side:
373⋅L2=273⋅L2+1365
- Rearranging gives:
373L−273L=2730
- Simplifying:
100L=2730
- Thus:
L=2730100=27.3 cm
9. Final Calculation:
- The total length of the hollow cylinder is L+5=27.3+5=32.3 cm.
Final Answer:
The length of the hollow cylinder is 32.3 cm.
- We have a closed hollow insulated cylinder divided by a piston.
- One side of the piston contains gas at 0∘C (273 K) and the other side contains gas at 100∘C (373 K).
- The piston moves 5 cm when the gas on one side is heated.
- The ideal gas law states that PV=nRT, where P is pressure, V is volume, n is the number of moles, R is the gas constant, and T is the temperature in Kelvin.
- Since the cylinder is insulated, the pressure on both sides of the piston remains equal when the piston moves.
- Let the length of the cylinder be L.
- The volume on the left side (initial) is V1=A⋅L2 (where A is the cross-sectional area).
- The volume on the right side (after the piston moves) is V2=A⋅(L2+5).
- For the left side (initial state at 0∘C):
P1⋅A⋅L2=n1⋅R⋅273
- For the right side (final state at 100∘C):
P2⋅A⋅(L2+5)=n2⋅R⋅373
- Since the piston is in equilibrium, P1=P2.
- Thus, we can set the equations equal to each other:
P1⋅A⋅L2273=P2⋅A⋅(L2+5)373
- We can cancel A and P1 from both sides:
L/2273=(L2+5)373
- Cross-multiplying gives:
373⋅L2=273⋅(L2+5)
- Expanding the right side:
373⋅L2=273⋅L2+1365
- Rearranging gives:
373L−273L=2730
- Simplifying:
100L=2730
- Thus:
L=2730100=27.3 cm
- The total length of the hollow cylinder is L+5=27.3+5=32.3 cm.
The length of the hollow cylinder is 32.3 cm.
Topper's Solved these Questions
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Comprehension Type
5 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Fill in the blanks
8 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
Similar Questions
A vertical closed cylinder is separated into two parts by a frictionless piston of mass m and of negligible thickness. The piston is free to move along the length of the cylinder. The length of the cylinder above the piston is l1, and that below the piston is l2, such that l1>l2. Each part of the cylinder contains n moles of an ideal gas at equal temeprature T. If the pistion is stationary, its mass, m, will be given by : (R is universal gas constant and g is the acceleration due to gravitey)
View SolutionA masslesss piston divides a closed thermallyy insulated cylinder into two equal parts. One part contains M = 28 g of nitrogen. At this temperature, one-third of molecules are dissociated into atoms and the other part is evacuated. The piston is released and the gas fills the whole volume of the cylinder at temperature T0. Then, the piston is slowly displaced back to its initial position. calculate the increases in internal energy of the gas. Neglect further dissociation of molecules during, the motion of the piston.
View Solution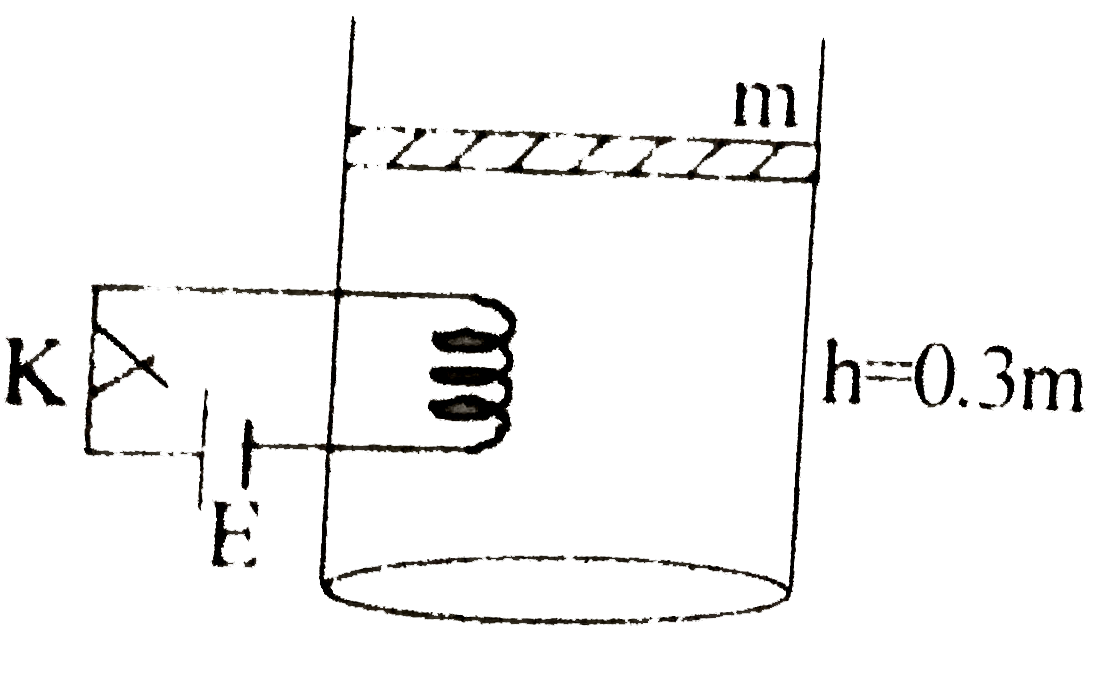
An insulated cylinder contains nitrogen gas which is sealed on the top by a heavy metal piston of mass m. piston is free to move with negligible friction, initial height of the piston is 0.3 m at temperature 27∘C when it is givenn some heat with the help of an electrical circuit piston slowly rises to height 0.5 m above the bottom of the cylinder. During expansion of te gas, net heat absorbed by the nitrogen gas:
View SolutionA vertical thermally insulated cylinder of volume V contain n moles of an ideal monoatomic gas under a weightless piston. A load of weight W is placed on the piston as a result of which the piston is displaced. If the initial temp of the gas is 300K, area of piston is A and atmospheric pressure P0. (take W=P0A). Determine the value of final temperature of the gas
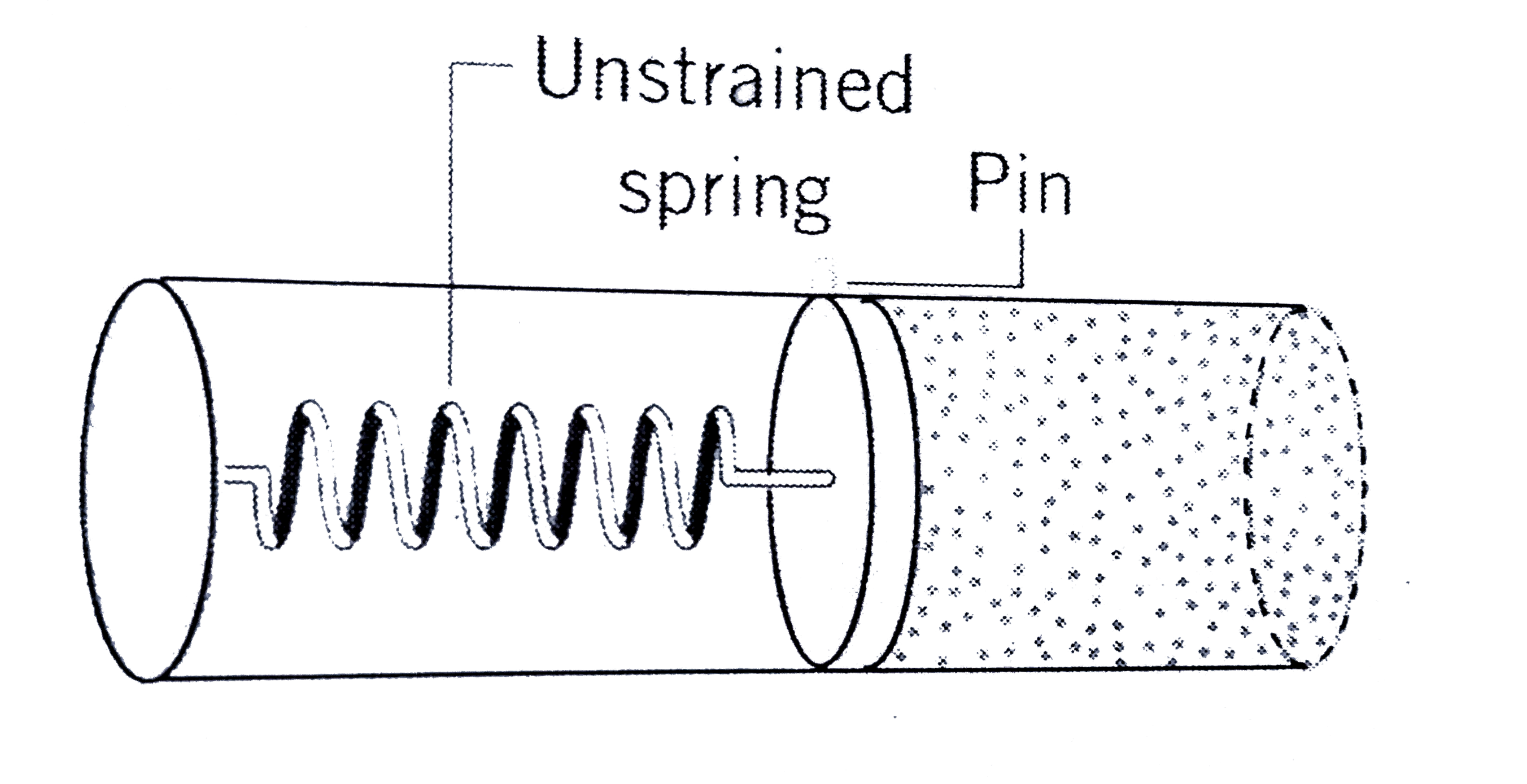
View SolutionA gas fills the right portion of a horizontal cylinder whose radius is 5.00cm. The initial pressure of the gas is 101kPa. A frictionless movable piston separates the gas from the left portion of the cylinder, which is evacuated and contains an ideal spring, as the drawing shows. The piston is initially unstrained, and the length of the gas-filled portion is 20.0cm. Wheen the pin is removed and the gas is allowed to expand, the length of the gas-filled chamber doubles when it finally reaches equilibrium. The initial and final temperatures are equal. Determine the spring constant of the spring.
View SolutionThe fixed non-conducting cylinder shown in figure has a noconducting heavy piston of mass M that can slide without friction. The area of piston is S and the cylinder is filled with an ideal gas (λ=1.5) with an initial volume V and an initial pressure P. Assume that the outside pressure on the piston is zero (vaccum). (Neglect acceleration due to gravity).
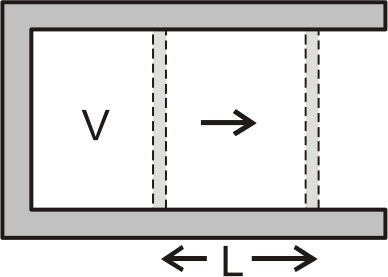
After the piston has moved by distance S. Its velocity is:
View SolutionA gas is contained in a metallic cylinder fitted with a piston.the piston is suddenly moved in to compress the gas and is maintained at this position. As time passes the pressure of the gas in the cylinder
View SolutionA gas is contained in a metallic cylinder fitted with a piston.The piston is suddenly moved in to compress the gas and is maintained at this position. As time passes the pressure of the gas in the cylinder
View SolutionA gas is contained in a metallic cylinder fitted with a piston.The piston is suddenly moved in to compress the gas and is maintained at this position. As time passes the pressure of the gas in the cylinder
View SolutionA weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V.2 moles of an ideal gas at pressure P=2 atmosphere are confined to the part with volume V=1 litre. The remainder of the cylinder is evacuated. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy in the process and final temperature of the gas. The ratio of the specific heats of the gas, γ=1.5.
View Solution
