Describe the motion of a particle acted upon by the force:
F=3x+3
F=−3x−3
F=−3x+3
F=−3x−3
The correct Answer is:A, B, C, D
To describe the motion of a particle acted upon by the given force equations, we can analyze the forces and their graphical representations step by step.
Step 1: Identify the Force Equations
The force equations given are:
1. F=3x+3
2. F=−3x−3
3. F=−3x+3
4. F=−3x−3
Step 2: Analyze Each Force Equation
For each force equation, we will analyze how the force varies with position x.
1. For F=3x+3:
- When x=0, F=3.
- When x=1, F=6.
- The force increases linearly as x increases.
- Graph: A straight line with a positive slope, starting from (0,3).
2. For F=−3x−3:
- When x=0, F=−3.
- When x=1, F=−6.
- The force decreases linearly as x increases.
- Graph: A straight line with a negative slope, starting from (0,−3).
3. For F=−3x+3:
- When x=0, F=3.
- When x=1, F=0.
- The force decreases linearly and crosses the x-axis.
- Graph: A straight line with a negative slope, starting from (0,3) and crossing the x-axis at (1,0).
4. For F=−3x−3 (same as the second):
- The analysis is the same as the second equation.
- Graph: A straight line with a negative slope, starting from (0,−3).
Step 3: Determine the Motion of the Particle
The motion of the particle can be described based on the force acting on it:
- Positive Force: When the force is positive (like in the first equation), the particle will accelerate in the positive direction.
- Negative Force: When the force is negative (like in the second and fourth equations), the particle will accelerate in the negative direction.
- Equilibrium: In the third equation, the force becomes zero at x=1, indicating a point of equilibrium where the particle may oscillate.
Conclusion
The particle's motion will vary depending on the force acting on it as described by the equations. The graphical representation helps visualize how the force changes with position, indicating the direction and nature of the particle's motion.
---
The force equations given are:
1. F=3x+3
2. F=−3x−3
3. F=−3x+3
4. F=−3x−3
For each force equation, we will analyze how the force varies with position x.
- When x=0, F=3.
- When x=1, F=6.
- The force increases linearly as x increases.
- Graph: A straight line with a positive slope, starting from (0,3).
- When x=0, F=−3.
- When x=1, F=−6.
- The force decreases linearly as x increases.
- Graph: A straight line with a negative slope, starting from (0,−3).
- When x=0, F=3.
- When x=1, F=0.
- The force decreases linearly and crosses the x-axis.
- Graph: A straight line with a negative slope, starting from (0,3) and crossing the x-axis at (1,0).
- The analysis is the same as the second equation.
- Graph: A straight line with a negative slope, starting from (0,−3).
The motion of the particle can be described based on the force acting on it:
- Negative Force: When the force is negative (like in the second and fourth equations), the particle will accelerate in the negative direction.
- Equilibrium: In the third equation, the force becomes zero at x=1, indicating a point of equilibrium where the particle may oscillate.
The particle's motion will vary depending on the force acting on it as described by the equations. The graphical representation helps visualize how the force changes with position, indicating the direction and nature of the particle's motion.
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct Answer Type
29 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type
5 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Integer
10 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
Describe the motion of a particle acted upon by a force
(i) F=−2(x−2)3
(ii) F=−2(x−2)2
(iii) F=−2(x−2)
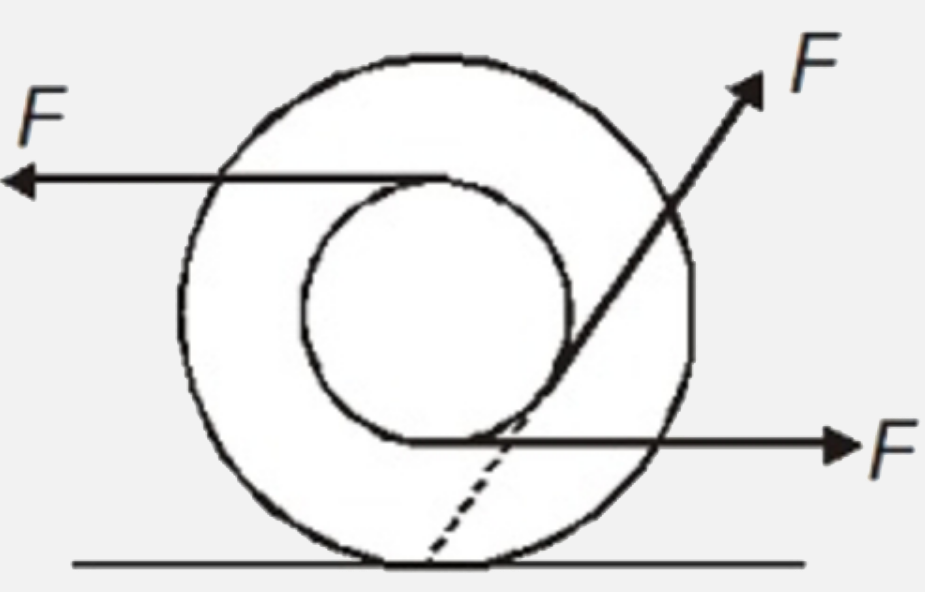
View SolutionConsider the following diagram. In which direction, the motion of the spool of thread (acted upon by three forces shown) kept over a perfectly rough horizontal surface will take place ?
View Solution
Knowledge Check
Given below are four curves describing variation of velocity with time of a particle. Which one of these describe the motion of a particle initially in positive direction with constant negative acceleration?
 A(W)B(X)C(Y)D(Z)
A(W)B(X)C(Y)D(Z)Assertion: The motion of a particle under the central force is always confined to a plane.
Reason: Angular momentum is always conserved in the motion under a central force.AIf both assertion and reason are true and reason is the correct explanation of assertionBIf both assertion and reason are truebut reason is not the correct explanation of assertionCIf assertion is true but reason is falseDIf both assertion and reason are false.A particle is acted upon by a force of constant magnitude which is always perpendicular to the velocity of the particle. The motion of the particle takes place in a plane. It follows that
Aits velocity is constantBits acceleration is constantCits kinetic energy is constantDit moves in a straight line.
A body is acted upon by balanced forces
View SolutionA particle is acted upon by a force of constant magnitude which is always perpendiculr to the velocity of the particle. The motion of the particle takes place in a plane. It follows that
View SolutionA particle is acted upon by a force of constant magnitude which is always perpendiculr to the velocity of the particle. The motion of the particle takes place in a plane. It follows that
View SolutionA particle is acted upon by a force of constant magnitude which is always perpendicular to the velocity of the particle. The motion of the particle takes place in a plane. It follows that
View SolutionA particle is acted upon by a force of constant magnitude which is always perpendicular to the velocity of the particle. The motion of the particle takes place in a plane. It follows that
View Solution
