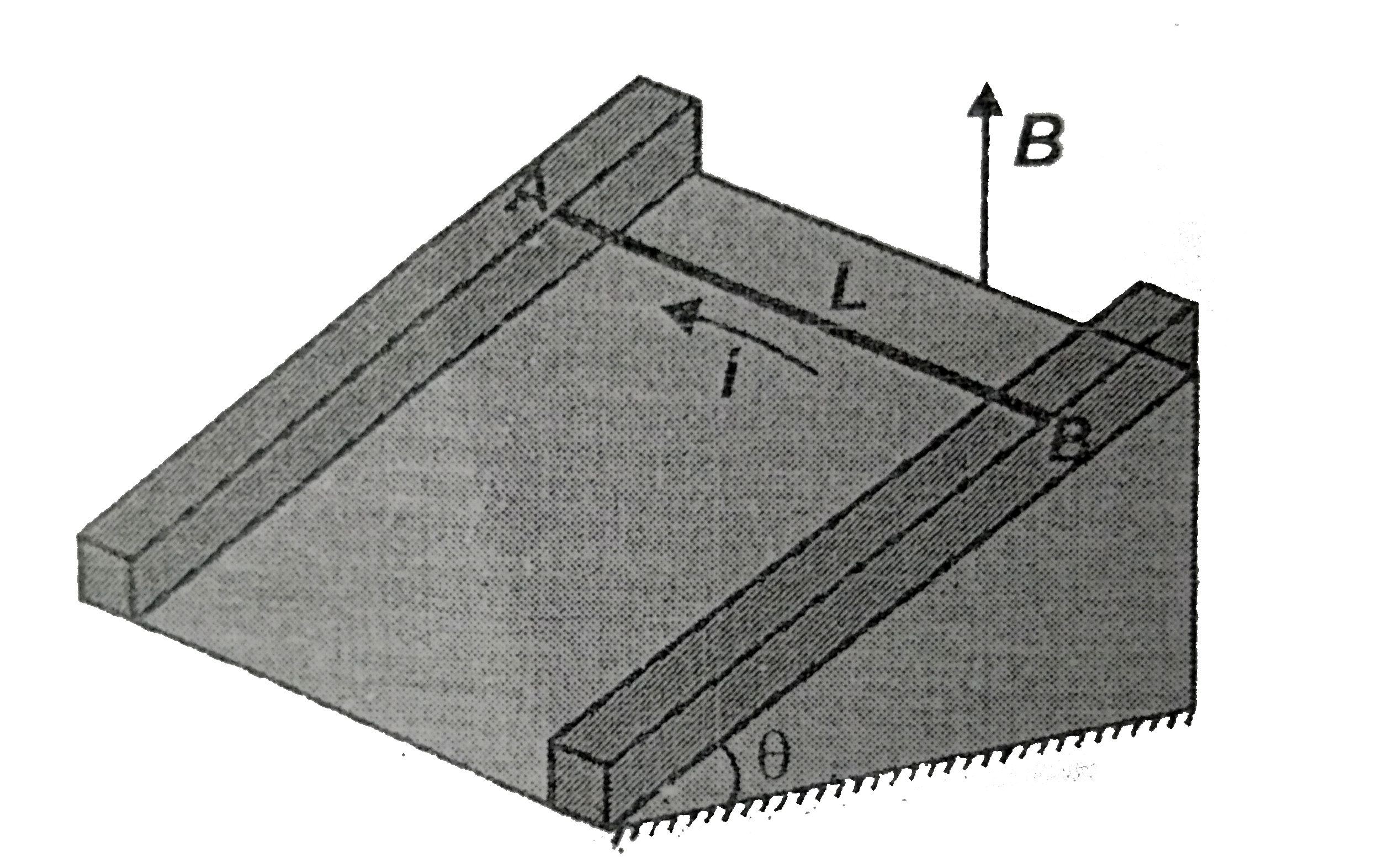
A copper rod of mass m rests on two horizontal rails distance L apart and carries a current of I from one rail to the other. The coefficient of static friction between rod and rails is μs What are the (a) magnitude and (b) angle (relative to the vertical) of the smallest magnetic field that puts the rod on the verge of sliding?
The correct Answer is:(a)0.10T(b)31∘
To solve the problem step by step, we will analyze the forces acting on the copper rod and derive the necessary equations to find the magnitude and angle of the magnetic field required to put the rod on the verge of sliding.
Step 1: Understand the Forces Acting on the Rod
The copper rod is resting on two horizontal rails and carries a current I. The forces acting on the rod include:
- The gravitational force mg acting downward.
- The magnetic force due to the current in the rod, which can be resolved into horizontal and vertical components based on the angle θ of the magnetic field B.
Step 2: Identify the Magnetic Force Components
The magnetic force FB acting on the rod can be calculated using the formula:
FB=I⋅B⋅L
Where:
- I is the current,
- B is the magnetic field strength,
- L is the length of the rod (distance between the rails).
The force can be resolved into two components:
- Horizontal component: FB,x=IBLsin(θ)
- Vertical component: FB,y=IBLcos(θ)
Step 3: Write the Equilibrium Conditions
For the rod to be on the verge of sliding, the horizontal magnetic force must equal the maximum static friction force:
FB,x=μsN
Where N is the normal force acting on the rod.
Step 4: Determine the Normal Force
The normal force N is the sum of the gravitational force and the vertical magnetic force:
N=mg+FB,y=mg+IBLcos(θ)
Step 5: Substitute the Normal Force into the Friction Equation
Substituting N into the friction equation gives:
IBLsin(θ)=μs(mg+IBLcos(θ))
Step 6: Rearrange the Equation
Rearranging the equation leads to:
IBLsin(θ)=μsmg+μsIBLcos(θ)
IBLsin(θ)−μsIBLcos(θ)=μsmg
Factoring out IBL gives:
IBL(sin(θ)−μscos(θ))=μsmg
Step 7: Solve for the Magnetic Field B
From the above equation, we can express B:
B=μsmgIL(sin(θ)−μscos(θ))
Step 8: Find the Angle θ
To minimize B, we need to maximize the denominator sin(θ)−μscos(θ). Taking the derivative and setting it to zero gives:
ddθ(sin(θ)−μscos(θ))=0
This leads to:
cos(θ)+μssin(θ)=0
Thus, we find:
tan(θ)=−μs
Since we are interested in the magnitude, we have:
tan(θ)=μs
Step 9: Substitute θ Back to Find B
Substituting tan(θ)=μs into the equation for B:
B=μsmgIL(μs√1+μ2s−μs1√1+μ2s)
This simplifies to:
B=μsmg√1+μ2sIL
Final Answers
(a) The magnitude of the magnetic field B:
B=μsmg√1+μ2sIL
(b) The angle θ relative to the vertical:
θ=tan−1(μs)
The copper rod is resting on two horizontal rails and carries a current I. The forces acting on the rod include:
- The gravitational force mg acting downward.
- The magnetic force due to the current in the rod, which can be resolved into horizontal and vertical components based on the angle θ of the magnetic field B.
The magnetic force FB acting on the rod can be calculated using the formula:
FB=I⋅B⋅L
Where:
- I is the current,
- B is the magnetic field strength,
- L is the length of the rod (distance between the rails).
- Horizontal component: FB,x=IBLsin(θ)
- Vertical component: FB,y=IBLcos(θ)
For the rod to be on the verge of sliding, the horizontal magnetic force must equal the maximum static friction force:
FB,x=μsN
Where N is the normal force acting on the rod.
The normal force N is the sum of the gravitational force and the vertical magnetic force:
N=mg+FB,y=mg+IBLcos(θ)
Substituting N into the friction equation gives:
IBLsin(θ)=μs(mg+IBLcos(θ))
Rearranging the equation leads to:
IBLsin(θ)=μsmg+μsIBLcos(θ)
IBLsin(θ)−μsIBLcos(θ)=μsmg
Factoring out IBL gives:
IBL(sin(θ)−μscos(θ))=μsmg
From the above equation, we can express B:
B=μsmgIL(sin(θ)−μscos(θ))
To minimize B, we need to maximize the denominator sin(θ)−μscos(θ). Taking the derivative and setting it to zero gives:
ddθ(sin(θ)−μscos(θ))=0
This leads to:
cos(θ)+μssin(θ)=0
Thus, we find:
tan(θ)=−μs
Since we are interested in the magnitude, we have:
tan(θ)=μs
Substituting tan(θ)=μs into the equation for B:
B=μsmgIL(μs√1+μ2s−μs1√1+μ2s)
This simplifies to:
B=μsmg√1+μ2sIL
(a) The magnitude of the magnetic field B:
B=μsmg√1+μ2sIL
θ=tan−1(μs)
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Comphension Based
2 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
A conductor (rod) of mass m, length l carrying a current i is subjected to a magnetic field of induction B. If the coefficients of friction between the conducting rod and rail is μ, find the value of I if the rod starts sliding.
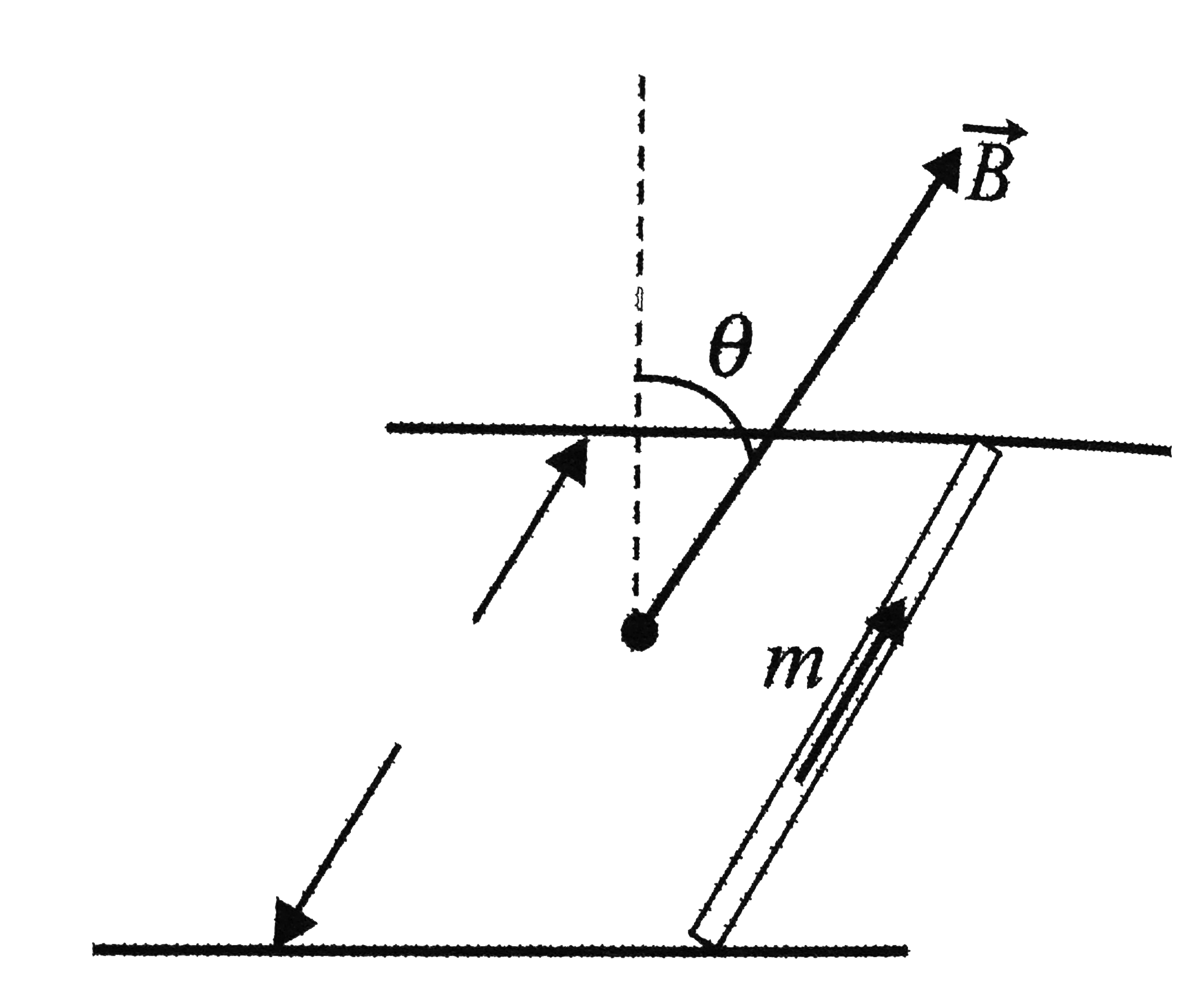
View SolutionA copper rod of mass m slides under gravity on two smooth parallel rails l distance apart set at an angle θ to the horizontal. At the bottom, the rails are joined by a resistance R.

There is a uniform magnetic field perpendicular to the plane of the rails. the terminal valocity of the rod is
View SolutionA straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is μ. If the wire carries a current I, what minimum magnetic field should exist in the space in order to slide the wire on the rails.
View SolutionOn an inclined plane, two conducting rails are fixed along the line of greatest slope. A conducting rod AB is placed on the radils so that it is horizontal. A vertically upward uniform magnetic field is present in the region. A current i flows through AB from B to A. The mass of AB is m and the coefficient of friction between the rod and rails is μ. Find the minimum and maximum value of B, so that the rod can stay in equilibrium. Assume that μ<tanθ
View SolutionShows two long metal rails placed horizontally and parallel to each other at a separation i. A uniform magnetic field b exists in the vertically downward direction. A wire of mass m can slide on the rails. The rails are connected to a constant current source which drives a current I in the circuirt. The friction coefficient between the rails and the wire is μ. (a) What should be the minimum value of μ which can prevent the wire from sliding on the rails? (b) Describe the motion of the wire if the value of μ is half the value found in the previous part.

View SolutionTwo hemispheres of radii R and r(<R) are fixed on a horizontal table touching each other (see figure). A uniform rod rests on to spheres as shown. The coefficient of friction between the rod and two spherers is μ. Then the maximum value of the ratio rR for which the rod will not slide is :

View Solution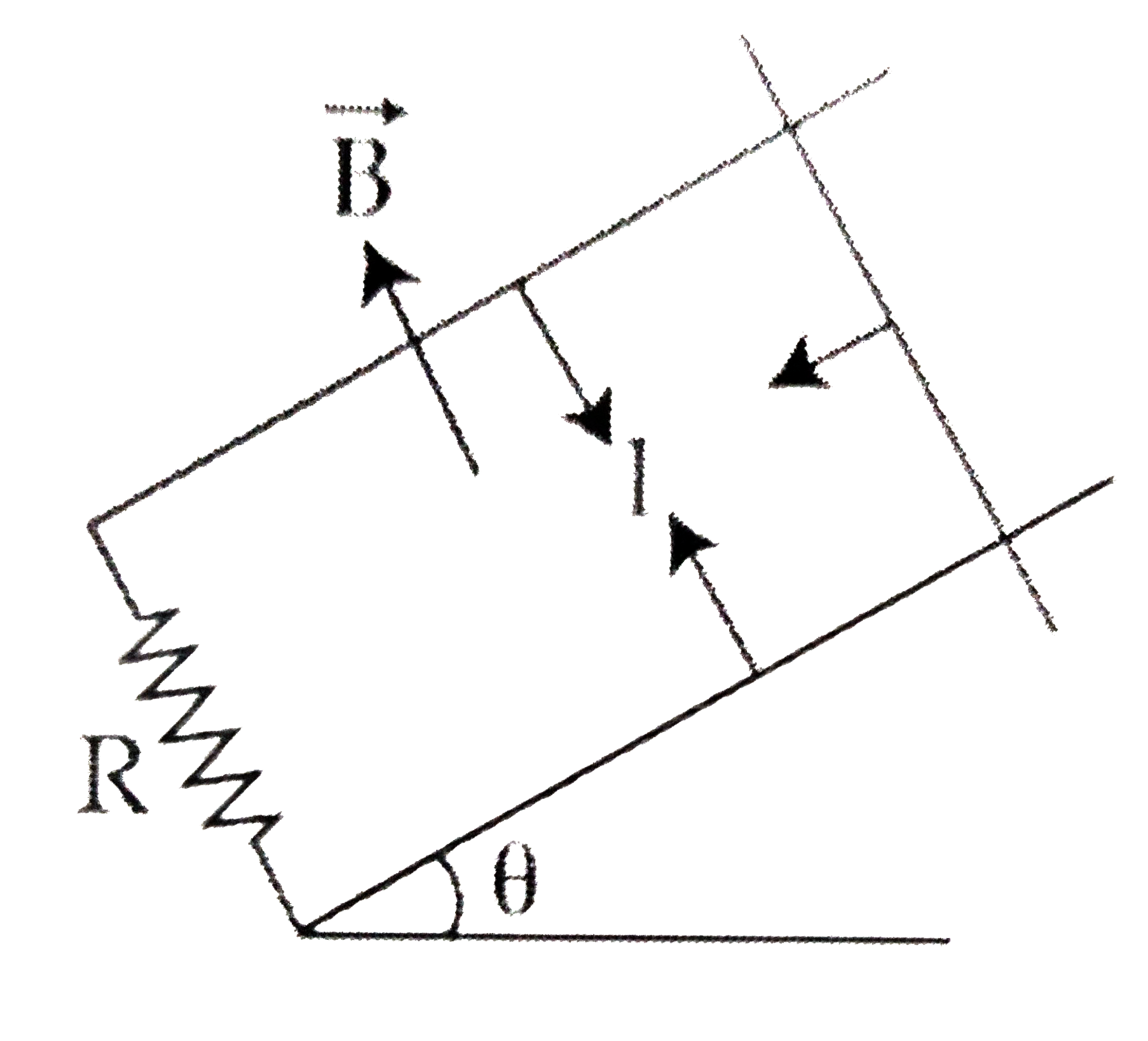
a copper rod of mass m slides under gravity on two smooth parallel rails with separation I and set at an angle of θ with the horiziontal at the bottom rails are joined by resistance R. There is a uniform magnetic field B normal to the plane of the rails as shown in the figure The terminal speed of the copper rod is :
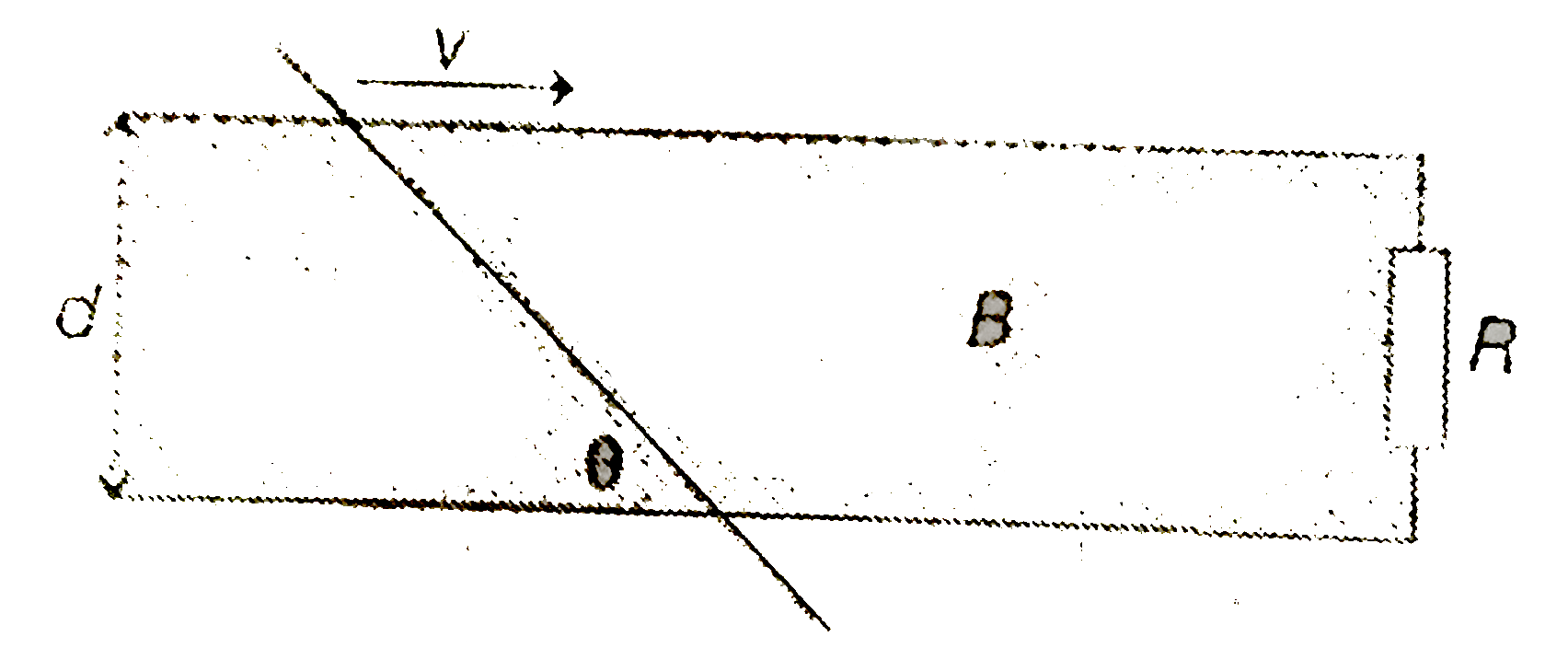
View SolutionA conducting rod with resistance r per unit length is moving inside a vertical magnetic field B with speed v on two smooth horizontal parallel ideal conducting rails. The end of the rails are connected to a resistor R. the separation between the rails is d. The rod maintains a tilted angle θ to the rail. Find the external force F required to keep the rod moving
View SolutionA conducting rod of length 'l'=2√5 meter and mass 'm'=4kg lies on the horizontal table. Coefficient of friction between the rod and the table is 'μ'=(12). If the current in the conductor si 2 ampere, then find the minimum magnitude of magnetic field strength (in Tesla) such that conducting rod just starts to translate along x -axis (take g=10m/sec2) [neglect the radius of rod]

View SolutionA rod of mass 0.720 kg and radius 6 cm rests on two parallel rails that are d=12cm apart and length of rails is L=49cm. The rod carried a current of I=48A Fig. and rolls along the rails without slipping. A uniform magnetic field of magnetude 0.240 T is directed perpendicular to the rod and the rails. If it starts from rest, what is the speed of the rod as it leaves the rails?

View Solution
