A player with 3 meter long iron rod runs toward east with a speed of 30km/hr . Horizontal component of eath's magnetic field is 4×10−5Wb/m2 . If he runs with the rod in horizontal and vertical position, then the potential difference induced between the two ends of the rod in the two cases will be
Zero in vertical position and 1×10−3 V in horizontal position
1×10−3 V in vertical position and zerp is horizontal position
Zero in both cases
1×10−3 V in both cases
The correct Answer is:b
To solve the problem of the induced potential difference in the iron rod when it is running horizontally and vertically, we can follow these steps:
Step 1: Convert the speed from km/hr to m/s
The speed of the player is given as 30 km/hr. To convert this to meters per second (m/s), we use the conversion factor:
1 km/hr=13.6 m/s
Thus,
30 km/hr=303.6 m/s≈8.33 m/s
Step 2: Identify the magnetic field and rod length
The horizontal component of the Earth's magnetic field is given as:
B=4×10−5 Wb/m2
The length of the rod is:
L=3 m
Step 3: Analyze the two positions of the rod
1. Horizontal Position: When the rod is held horizontally, the angle θ between the velocity vector and the magnetic field is 90 degrees (since the rod is moving east and the magnetic field is directed north). The induced EMF (E) can be calculated using the formula:
E=B⋅L⋅v⋅sin(θ)
Here, sin(90∘)=1:
Ehorizontal=B⋅L⋅v=(4×10−5)⋅(3)⋅(8.33)
Ehorizontal=1×10−3 V=1 mV
2. Vertical Position: When the rod is held vertically, the angle θ between the velocity vector and the magnetic field is 0 degrees. Thus:
Evertical=B⋅L⋅v⋅sin(0∘)=0
Therefore, no EMF is induced when the rod is vertical.
Final Results
- Induced potential difference when the rod is horizontal: 1 mV
- Induced potential difference when the rod is vertical: 0 V
Conclusion
The potential difference induced between the two ends of the rod is:
- Horizontal position: 1×10−3 V
- Vertical position: 0 V
Thus, the correct option is Option 2: 1×10−3 V in vertical position and 0 in horizontal.
The speed of the player is given as 30 km/hr. To convert this to meters per second (m/s), we use the conversion factor:
1 km/hr=13.6 m/s
Thus,
30 km/hr=303.6 m/s≈8.33 m/s
The horizontal component of the Earth's magnetic field is given as:
B=4×10−5 Wb/m2
The length of the rod is:
L=3 m
1. Horizontal Position: When the rod is held horizontally, the angle θ between the velocity vector and the magnetic field is 90 degrees (since the rod is moving east and the magnetic field is directed north). The induced EMF (E) can be calculated using the formula:
E=B⋅L⋅v⋅sin(θ)
Here, sin(90∘)=1:
Ehorizontal=B⋅L⋅v=(4×10−5)⋅(3)⋅(8.33)
Ehorizontal=1×10−3 V=1 mV
Evertical=B⋅L⋅v⋅sin(0∘)=0
Therefore, no EMF is induced when the rod is vertical.
- Induced potential difference when the rod is horizontal: 1 mV
- Induced potential difference when the rod is vertical: 0 V
The potential difference induced between the two ends of the rod is:
- Horizontal position: 1×10−3 V
- Vertical position: 0 V
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - comprehensive
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - single correct
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Multiple correct Answer Type
3 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
The horizontal component of earth's magnetic field is 3×10−5Wb/m2. The magnetic flux linked with a coil of area 1m2 and having 5 turns, whose plane is normal to the magnetic field, will be
View SolutionA jet plane having a wing-span of 25 m is travelling horizontally towards East with a speed of 3600 km /hr. If the Earth's magnetic field at the location is 4××10−4 T and the angle of dip is 30∘ , then the potential difference between the ends of the wing is
View SolutionA helicopter rises vertically upwards with a speed of 100 m/s. If the helicopter has a length of 10m and horizontal component of earth's magnetic field is 5×10−3Wb/m2, then the induced emf between the tip of the nose and the tail of the helicopter is
View SolutionA helicopter rises vertically upwards with a speed of 100 m/s. If the helicopter has a length of 10m and horizontal component of earth's magnetic field is 5×10−3Wb/m2, then the induced emf between the tip of the nose and the tail of the helicopter is
View SolutionA horizontal straight wire 20 m long extending from east to west falling with a speed of 5.0m/s, at right angles to the horizontal component of the earth’s magnetic field 0.30×10–4Wb/m2. The instantaneous value of the e.m.f. induced in the wire will be
View SolutionThe horizontal component of the earth's magnetic field at any place is 0.36×10−4Wbm−2 If the angle of dip at that place is 60∘ then the value of the vertical component of earth's magnetic field will be ( in Wbm−2)
View SolutionA conducting rod of length l is hinged at point O. It is a free to rotate in a verical plane. There exists a uniform magnetic field B in horizontal direction. The rod is released from the position shown. The potential difference between the two ends of the rod is proportional to
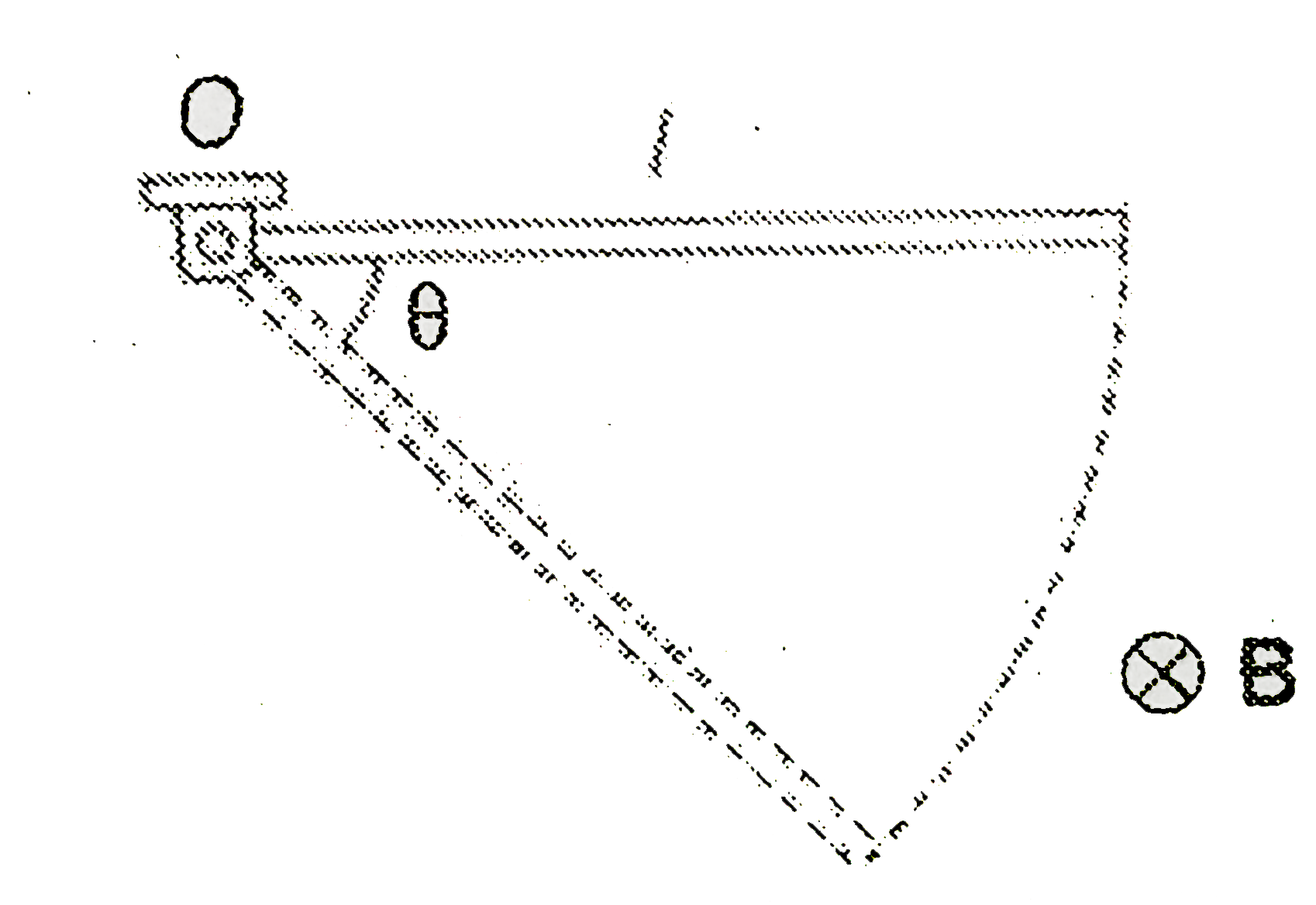
View SolutionA horizontal straight wire 10 m long extending from east to west falling with a speed of 0.5 ms−1 at right angles to the horizontal component of the earth's magnetic field 0.30×10−4Wbm−2
(a) What is the instantaneous value of the e.m.f. induced in the wire ?
(b) What is the direction value of the e.m.f. (c) Which end of the wire is at higher electric potential ?
View SolutionAn aeroplane in which the distance between the tips of wings is 50m is flying horizontal with a speed of 360km/hr over a place where the verticle components of earth magnetic field is 2.0×10−4webr/m2. The potential different between the tips of wings would be
View SolutionA horizontal straight wire 10m long extending from east to west is falling with a speed of 5.0m/s at right angles to the horizontal component of earths magnetic field 0.3xx10^(-4) tesla. The emf induced across the ends of wire is
View Solution