In a series L-R circuit, connected with a sinusoidal ac source, the maximum potential difference across L and R are respectivaly 3 volts and 4 volts.
At an instant the potemtial difference across resistor is 2 volts. The potential difference in volt, across the inductor at the same instant will be:
3cos30∘
3cos50∘
6cos45∘
6
The correct Answer is:A
To solve the problem step by step, we will analyze the given information and apply the relevant concepts of alternating current in an L-R circuit.
Step 1: Identify the maximum potential differences
We are given:
- Maximum potential difference across the resistor (V₀_R) = 4 volts
- Maximum potential difference across the inductor (V₀_L) = 3 volts
Step 2: Write the expressions for instantaneous voltages
In a series L-R circuit, the instantaneous voltage across the resistor (V_R) and the inductor (V_L) can be expressed as:
- VR=V₀R⋅sin(ωt)
- VL=V₀L⋅cos(ωt)
Here, sin(ωt) represents the phase of the voltage across the resistor, and cos(ωt) represents the phase of the voltage across the inductor, which leads the current by 90 degrees.
Step 3: Use the given instantaneous voltage across the resistor
At a certain instant, the potential difference across the resistor is given as:
- VR=2 volts
Using the expression for VR:
2=4⋅sin(ωt)
From this, we can solve for sin(ωt):
sin(ωt)=24=12
Step 4: Determine the value of cos(ωt)
Using the Pythagorean identity:
sin2(ωt)+cos2(ωt)=1
Substituting the value of sin(ωt):
(12)2+cos2(ωt)=1
14+cos2(ωt)=1
cos2(ωt)=1−14=34
Taking the square root:
cos(ωt)=√34=√32
Step 5: Calculate the instantaneous voltage across the inductor
Now we can find the instantaneous voltage across the inductor using the expression for VL:
VL=V₀L⋅cos(ωt)
Substituting the known values:
VL=3⋅√32=3√32 volts
Final Answer
The potential difference across the inductor at that instant is 3√32 volts.
---
We are given:
- Maximum potential difference across the resistor (V₀_R) = 4 volts
- Maximum potential difference across the inductor (V₀_L) = 3 volts
In a series L-R circuit, the instantaneous voltage across the resistor (V_R) and the inductor (V_L) can be expressed as:
- VR=V₀R⋅sin(ωt)
- VL=V₀L⋅cos(ωt)
At a certain instant, the potential difference across the resistor is given as:
- VR=2 volts
2=4⋅sin(ωt)
From this, we can solve for sin(ωt):
sin(ωt)=24=12
Using the Pythagorean identity:
sin2(ωt)+cos2(ωt)=1
Substituting the value of sin(ωt):
(12)2+cos2(ωt)=1
14+cos2(ωt)=1
cos2(ωt)=1−14=34
Taking the square root:
cos(ωt)=√34=√32
Now we can find the instantaneous voltage across the inductor using the expression for VL:
VL=V₀L⋅cos(ωt)
Substituting the known values:
VL=3⋅√32=3√32 volts
The potential difference across the inductor at that instant is 3√32 volts.
Topper's Solved these Questions
- ALTERNATING CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:ALTERNATING CURRENTExercise:Single Correct
Explore 10 Videos
- ALTERNATING CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:ALTERNATING CURRENTExercise:Single Correct Asnwer Type
Explore 27 Videos
- ATOMIC PHYSICSBook:CENGAGE PHYSICS ENGLISHChapter:ATOMIC PHYSICSExercise:ddp.4.3
Explore 15 Videos
Similar Questions
In a series L−R circuit, connected with a sinusoidal ac source, the maximum potential difference acrosssd L and R are respectively 3 volts and 4 volts
At the same instant, the magnitude of the potential difference in volt, across the ac source will be
View SolutionIn a series L−R circuit, connected with a sinusoidal ac source, the maximum potential difference acrosssd L and R are respectively 3 volts and 4 volts
If the current at this instant is decreasing the magnitude of potential difference at that instant across the ac source is
View SolutionIn the circuit shown, rms circuit is 11 A . The potential difference across the inductor is

View SolutionThe potential difference across 8 ohm resistance is 48 volt as shownin the figure. The value of potential difference across X and Y point will be
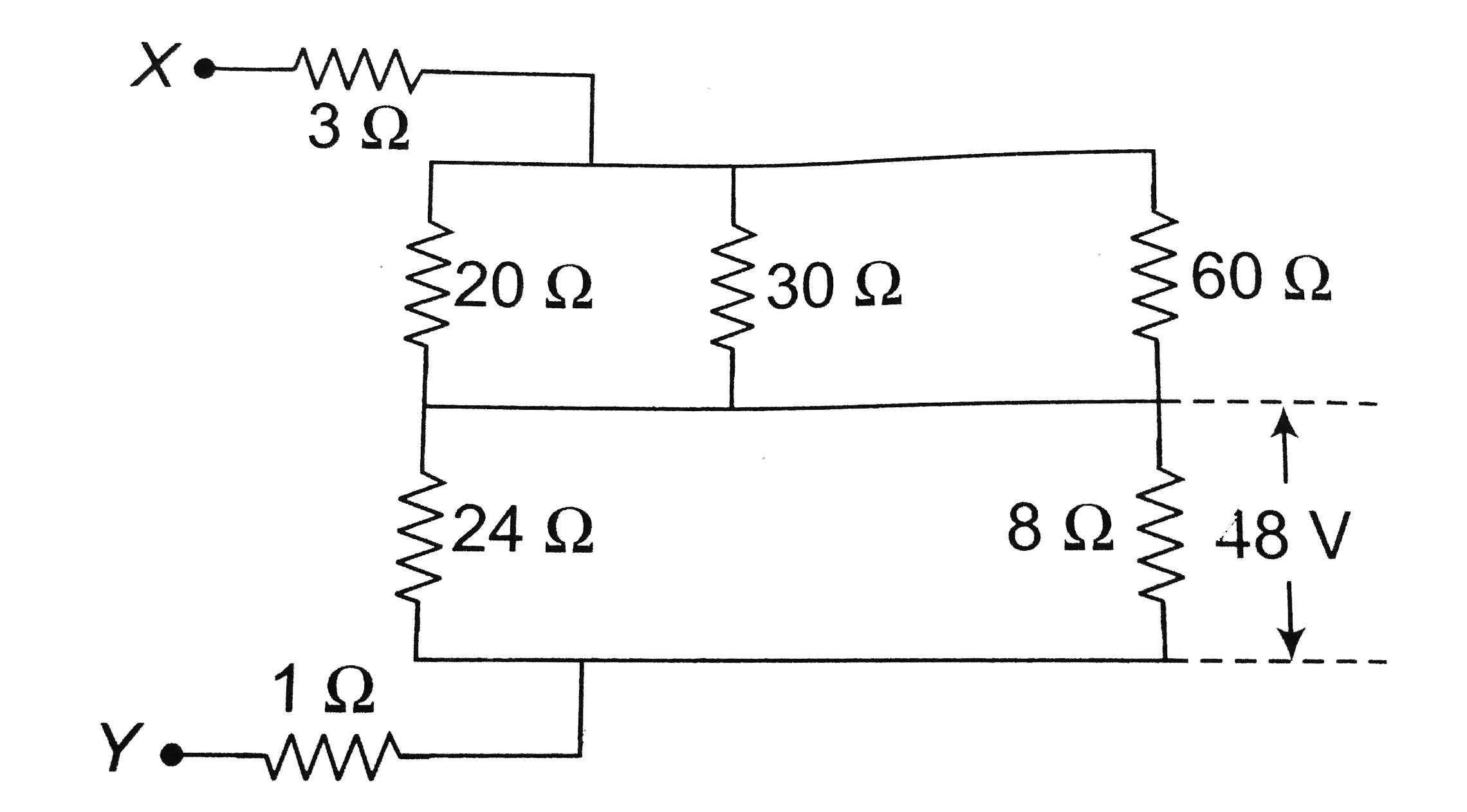
View SolutionThe potential difference across 8 ohm resistance is 48 volt as shownin the figure. The value of potential difference across X and Y point will be

View SolutionIn the circuit shown in figure potential difference across

View SolutionIn the shown circuit, what is the potential difference across A and B

View SolutionPotential difference across AB in the circuit as shown in figure.

View SolutionIn section PQ of a circuit P is at higher potential than Q by 40 V. The potential difference in volt across the battery A is:

View SolutionIn the circuit shown, what is the potential difference VPQ in volts ?

View Solution
