A photon of frequency n causes photoelectric emmission from a surface with threshold frequency n0 .The de Broglie wavelength λ of the photoelectron emitted is given as
Δn=h2mλ
Δn=hλ
[1v0−1v]=mc2n
λ=√h2mΔV
To solve the problem of finding the de Broglie wavelength λ of the photoelectron emitted due to photoelectric emission, we can follow these steps:
Step 1: Understand the Photoelectric Effect
The photoelectric effect occurs when photons strike a material and emit electrons. The energy of the incoming photon must be greater than the work function (or threshold energy) of the material for the emission to occur.
Step 2: Relate Photon Energy to Frequency
The energy E of a photon is given by the equation:
E=h⋅n
where h is Planck's constant and n is the frequency of the photon.
Step 3: Determine the Work Function
The work function ϕ (or threshold energy) is related to the threshold frequency n0 as:
ϕ=h⋅n0
Step 4: Calculate the Kinetic Energy of the Emitted Electron
The kinetic energy K.E. of the emitted electron can be expressed as:
K.E.=E−ϕ=h⋅n−h⋅n0=h(n−n0)
Step 5: Relate Kinetic Energy to Velocity
The kinetic energy of the electron can also be expressed in terms of its mass m and velocity v:
K.E.=12mv2
Setting the two expressions for kinetic energy equal gives:
h(n−n0)=12mv2
Step 6: Solve for Velocity
From the above equation, we can solve for the velocity v:
v=√2h(n−n0)m
Step 7: Use de Broglie Wavelength Formula
The de Broglie wavelength λ is given by:
λ=hp
where p is the momentum of the electron. The momentum p can be expressed as:
p=m⋅v
Substituting for v:
p=m⋅√2h(n−n0)m=√2hm(n−n0)
Step 8: Substitute Momentum into de Broglie Wavelength
Now substituting p into the de Broglie wavelength formula:
λ=h√2hm(n−n0)
This simplifies to:
λ=h√2hm⋅1√n−n0
Thus, we can express λ in terms of n and n0.
Final Answer
The de Broglie wavelength λ of the emitted photoelectron is given by:
λ=√h2m(n−n0)
The photoelectric effect occurs when photons strike a material and emit electrons. The energy of the incoming photon must be greater than the work function (or threshold energy) of the material for the emission to occur.
The energy E of a photon is given by the equation:
E=h⋅n
where h is Planck's constant and n is the frequency of the photon.
The work function ϕ (or threshold energy) is related to the threshold frequency n0 as:
ϕ=h⋅n0
The kinetic energy K.E. of the emitted electron can be expressed as:
K.E.=E−ϕ=h⋅n−h⋅n0=h(n−n0)
The kinetic energy of the electron can also be expressed in terms of its mass m and velocity v:
K.E.=12mv2
Setting the two expressions for kinetic energy equal gives:
h(n−n0)=12mv2
From the above equation, we can solve for the velocity v:
v=√2h(n−n0)m
The de Broglie wavelength λ is given by:
λ=hp
where p is the momentum of the electron. The momentum p can be expressed as:
p=m⋅v
Substituting for v:
p=m⋅√2h(n−n0)m=√2hm(n−n0)
Now substituting p into the de Broglie wavelength formula:
λ=h√2hm(n−n0)
This simplifies to:
λ=h√2hm⋅1√n−n0
Thus, we can express λ in terms of n and n0.
The de Broglie wavelength λ of the emitted photoelectron is given by:
λ=√h2m(n−n0)
Topper's Solved these Questions
- ATOMIC STRUCTUREBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercises (Subjective)
52 Videos
- ATOMIC STRUCTUREBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercises Linked Comprehension
50 Videos
- APPENDIX - INORGANIC VOLUME 1BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - APPENDIX - INORGANIC VOLUME 1EXERCISE - chapter-7 Single correct answer
1 Videos
- CHEMICAL BONDING AND MOLECULAR STRUCTUREBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTUREEXERCISE - Archives Subjective
15 Videos
Similar Questions
Knowledge Check
de Broglie wavelength of a moving particle is λ. Its momentum is given by :
AhλcBhλChcλDzerorepresents a graph of most energetic photoelectrons Kmax(in eV) and frequency v for a metal used as cathode in photoelectrons experiment. The threshold frequency of light for the photoelectric emission from the metal is
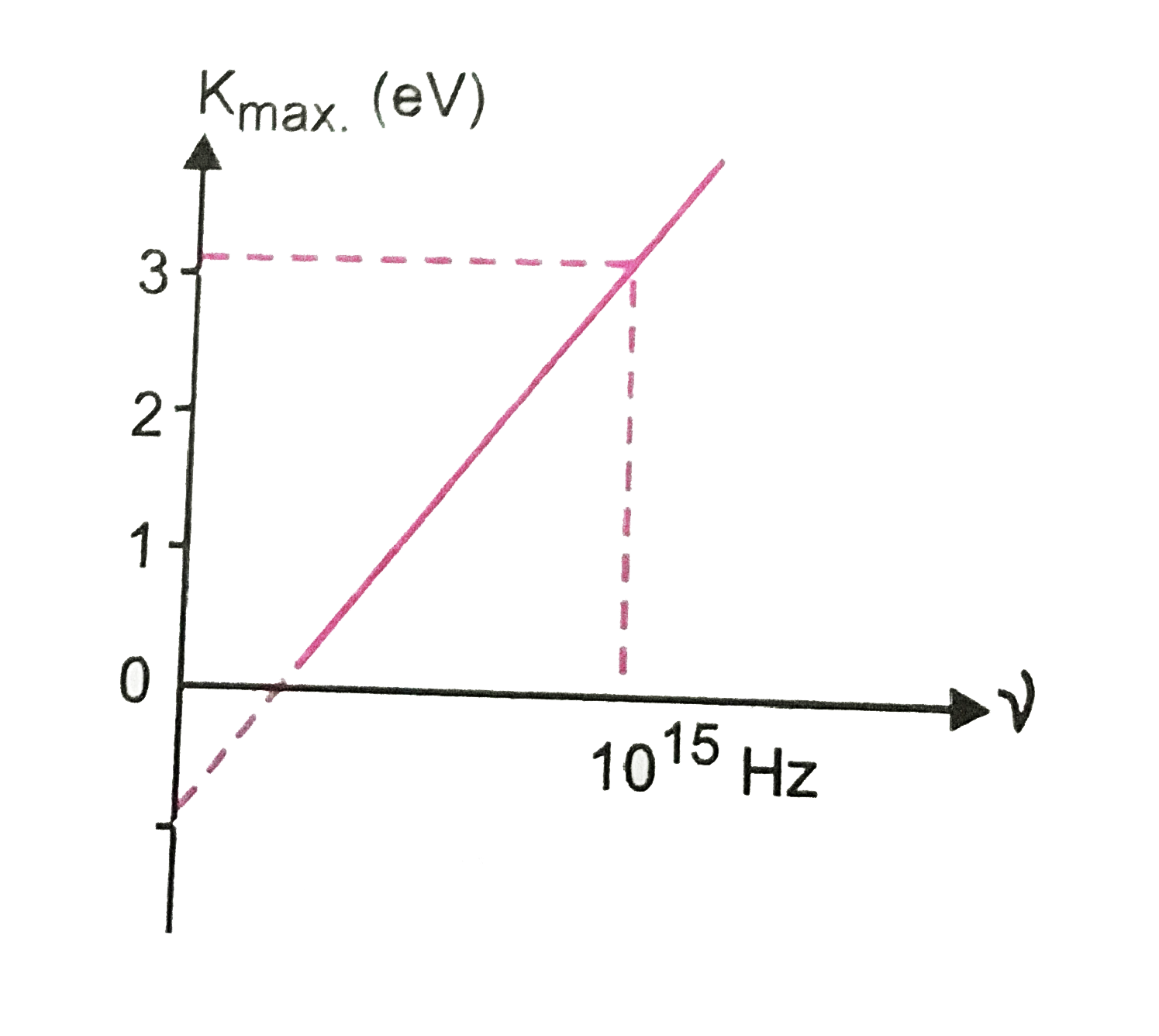 A1×1014HzB1.5×1014HzC2×1014HzD2.7×1014Hz
A1×1014HzB1.5×1014HzC2×1014HzD2.7×1014Hz
Electrons are emitted from the cathode of a photocell of negligible work function, when photons of wavelength λ are incident on it. Derive the expression for the de Broglie wavelength of the electrons emitted in terms of the wavelength of the incident light
View SolutionIf λ0 is the threshold wavelength for photoelectric emission. λ wavelength of light falling on the surface on the surface of metal, and m mass of electron. Then de Broglie wavelength of emitted electron is :-
View SolutionAn e-m wave of wavelength λ is incident on a photo sensitive surface of negligible work function. If the photoelectrons emitted from this surface have the de-Broglie wavelength λ1. Find relation between 'λ' and 'λ1'-
View SolutionPhoto electrons are liberated by ultraviolet light of wavelength 3000 Å from a metalic surface for which the photoelectric threshold wavelength is 4000Å. Calculate the de Broglie wavelength of electrons emitted with maximum kinetic energy.
View SolutionFor a proton accelerated through V volts , de Broglie wavelength is given as λ=
View SolutionA H−like species emitted a photon corresponding to the first line of Lyman series. The photon liberated a photoelectron from He+ ion in ground state. The de-brogile wavelength of the photoelectron is 2Å . Select the correct statement (s).
View Solution
