The second law of thermodynamics is a fundamental law of science. In this problem, we consider the thermodynamics of an ideal gas, phase transition, and chemical equilibrium.
Three moles of CO2 gas expands isothermally (in thermal contact with the surroundings, temperature =15.0∘C) against a fixed external pressure of 1.00 bar. The initial and final volumes of the gas are 10.0L and 30.0L, respectively.
ΔsurrS is
27.4JK−1
+6.94JK−1
0.00JK−1
−6.94JK−1
To solve the problem, we need to calculate the change in entropy of the surroundings (ΔSsurr) for the isothermal expansion of 3 moles of CO2 gas. The process is isothermal, meaning the temperature remains constant throughout the expansion.
1. Identify Given Data:
- Number of moles of CO2 (n) = 3 moles
- Initial volume (Vi) = 10.0 L
- Final volume (Vf) = 30.0 L
- External pressure (Pext) = 1.00 bar
- Temperature (T) = 15.0 °C = 288 K (convert to Kelvin by adding 273)
2. Calculate the Work Done (W):
The work done by the gas during expansion against a constant external pressure is given by:
W=−PextΔV
where ΔV=Vf−Vi=30.0L−10.0L=20.0L.
Convert pressure from bar to atm:
1bar≈0.9869atm
Therefore, Pext=1.00bar≈0.9869atm.
Now calculate the work:
W=−(0.9869atm)×(20.0L)=−19.738L atm
Convert W to Joules (1 L atm = 101.33 J):
W=−19.738×101.33J≈−1996.5J
3. Apply the First Law of Thermodynamics:
For an isothermal process, the change in internal energy (ΔU) is zero:
ΔU=Q+W⟹0=Q+W⟹Q=−W
Thus,
Q=1996.5J
4. Calculate the Change in Entropy of the Surroundings (ΔSsurr):
The change in entropy of the surroundings is given by:
ΔSsurr=−QT
Substituting the values:
ΔSsurr=−1996.5J288K≈−6.94J/K
5. Final Answer:
The change in entropy of the surroundings is:
ΔSsurr≈−6.94J/K
- Number of moles of CO2 (n) = 3 moles
- Initial volume (Vi) = 10.0 L
- Final volume (Vf) = 30.0 L
- External pressure (Pext) = 1.00 bar
- Temperature (T) = 15.0 °C = 288 K (convert to Kelvin by adding 273)
The work done by the gas during expansion against a constant external pressure is given by:
W=−PextΔV
where ΔV=Vf−Vi=30.0L−10.0L=20.0L.
1bar≈0.9869atm
Therefore, Pext=1.00bar≈0.9869atm.
W=−(0.9869atm)×(20.0L)=−19.738L atm
Convert W to Joules (1 L atm = 101.33 J):
W=−19.738×101.33J≈−1996.5J
For an isothermal process, the change in internal energy (ΔU) is zero:
ΔU=Q+W⟹0=Q+W⟹Q=−W
Thus,
Q=1996.5J
The change in entropy of the surroundings is given by:
ΔSsurr=−QT
Substituting the values:
ΔSsurr=−1996.5J288K≈−6.94J/K
The change in entropy of the surroundings is:
ΔSsurr≈−6.94J/K
Topper's Solved these Questions
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercises (Multiple Correct)50videos
THERMODYNAMICS
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Multiple correct Answer Type2videos
THERMODYNAMICS
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Paragraph for Problem1videos
THERMODYNAMICS
- BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STOICHIOMETRYEXERCISE - Archives Subjective33videos
STOICHIOMETRY
Similar Questions
The second law of thermodynamics is a fundamental law of science. In this problem, we consider the thermodynamics of an ideal gas, phase transition, and chemical equilibrium.
Three moles of CO2 gas expands isothermally (in thermal contact with the surroundings, temperature =15.0∘C) against a fixed external pressure of 1.00¯. The initial and final volumes of the gas are 10.0L and 30.0L, respectively.
Select the correct order of the entropy change.View SolutionThe second law of thermodynamics is a fundamental law of science. In this problem, we consider the thermodynamics of an ideal gas, phase transition, and chemical equilibrium.
Three moles of CO2 gas expands isothermally (in thermal contact with the surroundings, temperature =15.0∘C) against a fixed external pressure of 1.00¯. The initial and final volumes of the gas are 10.0L and 30.0L, respectively.
Assuming CO2 to be an ideal gas, ΔsysS isView Solution
Knowledge Check
- Question 1 - Select One
Under isothermal condition, a gas at 300 K expands from 0.1 L to 0.25 L against a constant external pressure of 2 bar. The work done by the gas is (Given that 1 L bar = 100 J)
A25 JB30 JC-30 JD5 kJ.
Three moles of CO2 gas expands isothermally (in thermal contact with the surroundings, temperature =15.0∘C) against a fixed external pressure of 1.00 bar. The initial and final volumes of the gas are 10.0L and 30.0L, respectively. ltbr> Change in entropy of the universe is
View Solutionone mole of an ideal gas at 300k in thermal contact with surroundings expands isothermally from 1.0 L to 2.0 L against a constant presses of 3.0 atm. In this process. The change in entropy of surrroundings (ΔS) in J−1 is
(1 L atm = 101.3 J)View SolutionAn ideal gas in a thermally insulated vessel at internal pressure =P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2 and T2 respectively. For this expansion.
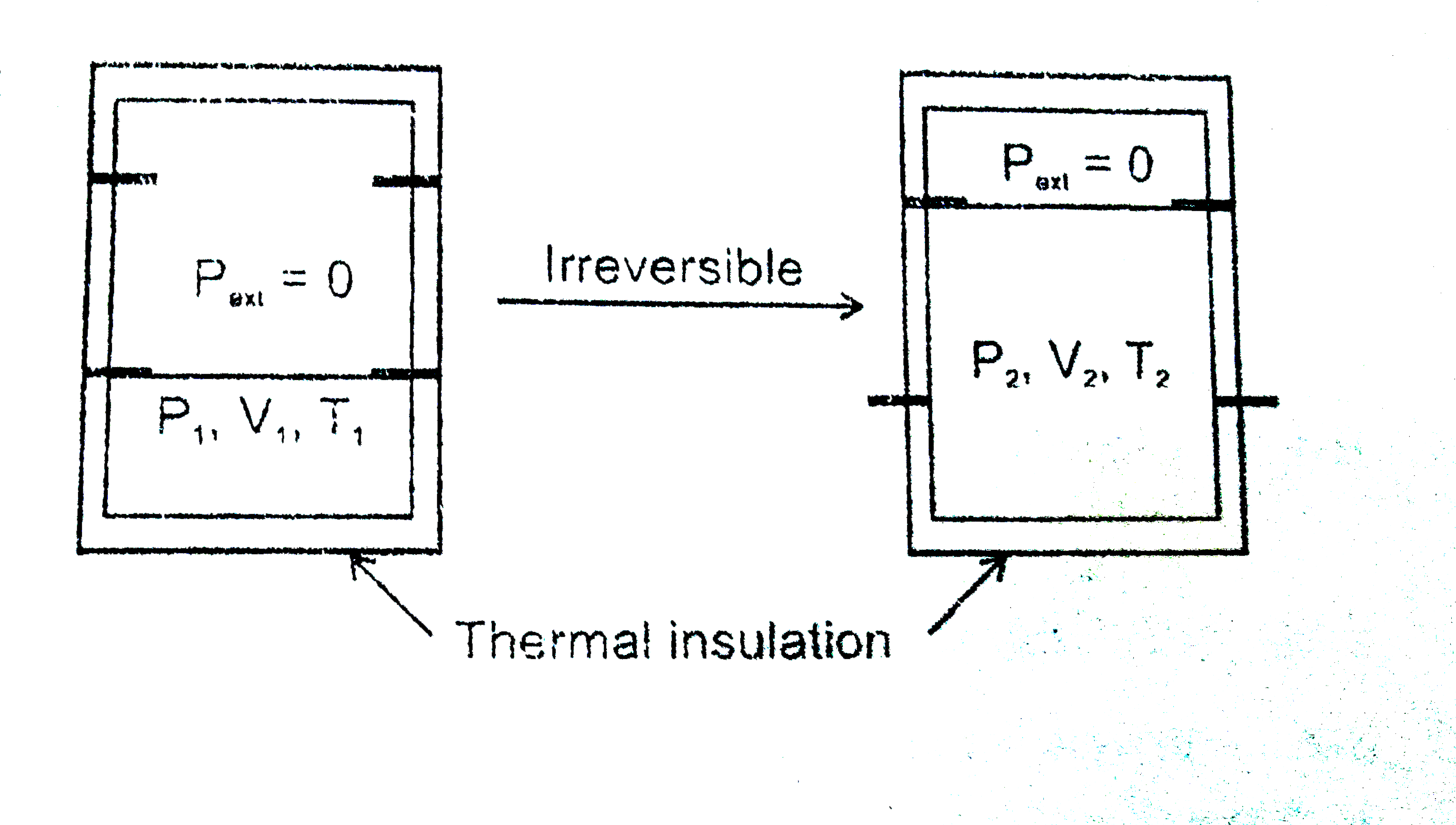 View Solution
View SolutionAn ideal gas in a thermally insulated vessel at internal pressure =P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2 and T2 respectively. For this expansion.
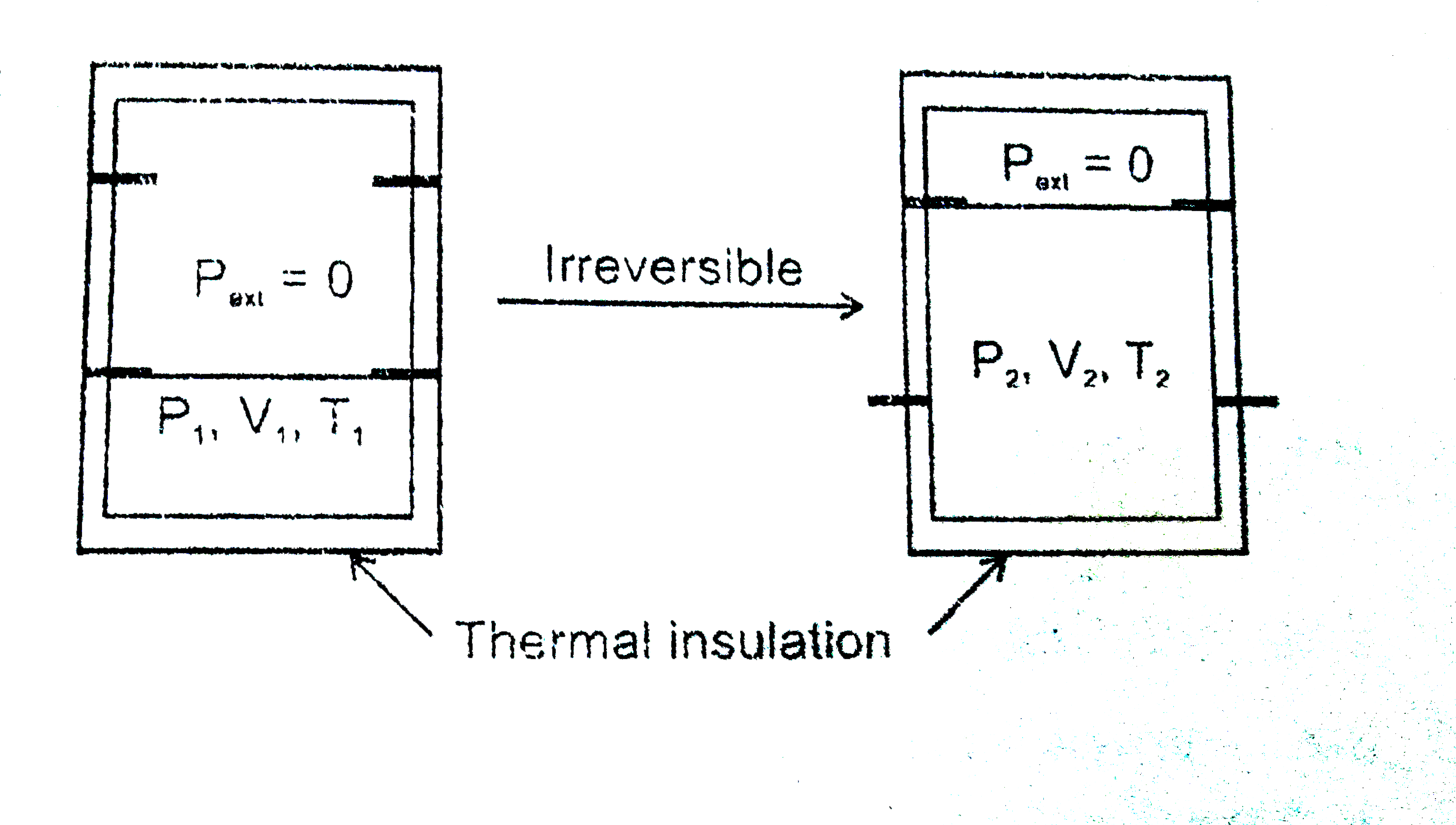 View Solution
View SolutionOne mole of an ideal monoatomic gas at temperature T and volume 1L expands to 2L against a constant external pressure of one atm under adiabatic conditions, then final temperature of gas will be:
View SolutionOne mole of an ideal monoatomic gas at temperature T and volume 1L expands to 2L against a constant external pressure of one atm under adiabatic conditions, then final temperature of gas will be:
View SolutionAn ideal gas in a thermally insulated vessel at internal pressure = P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2andT2, respectively. For this expansion.
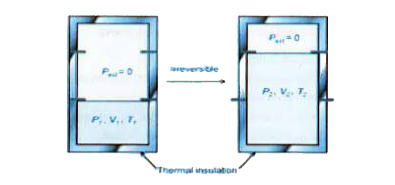 View Solution
View Solution

