Indicate in which case/cases the spontaneity of a change is favoured when
To determine the spontaneity of a change in thermodynamics, we need to analyze the Gibbs free energy change (ΔG) associated with the process. The spontaneity of a process is favored when ΔG is less than zero (ΔG < 0). Let's break down the steps to understand when this condition is met.
1. Understanding Spontaneity:
- A spontaneous process is one that occurs naturally without needing to be driven by an external force. For a process to be spontaneous, it must release free energy.
2. Gibbs Free Energy Equation:
- The Gibbs free energy change is given by the equation:
ΔG=ΔH−TΔS
- Where:
- ΔG = change in Gibbs free energy
- ΔH = change in enthalpy
- T = temperature (in Kelvin)
- ΔS = change in entropy
3. Condition for Spontaneity:
- For a process to be spontaneous, we need:
ΔG<0
- This implies:
ΔH−TΔS<0
- Rearranging gives:
ΔH<TΔS
4. Analyzing ΔH and ΔS:
- If ΔH is negative (exothermic reaction) and ΔS is positive (increase in disorder), then ΔG will definitely be negative, favoring spontaneity.
- If ΔH is positive (endothermic reaction) and ΔS is also positive, spontaneity can still occur at high temperatures where TΔS outweighs ΔH.
- If ΔH is negative and ΔS is negative, spontaneity occurs only at low temperatures where ΔH is more negative than TΔS.
- If ΔH is positive and ΔS is negative, the process is non-spontaneous at all temperatures.
5. Conclusion:
- Therefore, spontaneity is favored in the following cases:
- Case B: ΔH < 0 and ΔS > 0 (exothermic and increase in disorder)
- Case C: ΔH > 0 and ΔS > 0 (endothermic but increase in disorder at high temperatures)
- Case D: ΔH < 0 and ΔS < 0 (exothermic but decrease in disorder at low temperatures)
Final Answer:
The spontaneity of a change is favored in cases B, C, and D.
- A spontaneous process is one that occurs naturally without needing to be driven by an external force. For a process to be spontaneous, it must release free energy.
- The Gibbs free energy change is given by the equation:
ΔG=ΔH−TΔS
- Where:
- ΔG = change in Gibbs free energy
- ΔH = change in enthalpy
- T = temperature (in Kelvin)
- ΔS = change in entropy
- For a process to be spontaneous, we need:
ΔG<0
- This implies:
ΔH−TΔS<0
- Rearranging gives:
ΔH<TΔS
- If ΔH is negative (exothermic reaction) and ΔS is positive (increase in disorder), then ΔG will definitely be negative, favoring spontaneity.
- If ΔH is positive (endothermic reaction) and ΔS is also positive, spontaneity can still occur at high temperatures where TΔS outweighs ΔH.
- If ΔH is negative and ΔS is negative, spontaneity occurs only at low temperatures where ΔH is more negative than TΔS.
- If ΔH is positive and ΔS is negative, the process is non-spontaneous at all temperatures.
- Therefore, spontaneity is favored in the following cases:
- Case B: ΔH < 0 and ΔS > 0 (exothermic and increase in disorder)
- Case C: ΔH > 0 and ΔS > 0 (endothermic but increase in disorder at high temperatures)
- Case D: ΔH < 0 and ΔS < 0 (exothermic but decrease in disorder at low temperatures)
The spontaneity of a change is favored in cases B, C, and D.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Multiple correct Answer Type
2 Videos
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercises (Single Correct)
62 Videos
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercises (Linked Comprehension)
74 Videos
- STOICHIOMETRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STOICHIOMETRYEXERCISE - Archives Subjective
33 Videos
Similar Questions
Assertion (A): The thermodynamic factor which determines the spontaneity of a process is the free energy. For a process to be spontaneous the free energy must be-ve.
Reason (R ) : The change in free energy is related to the change in a process must always be positive if its is spontaneous.
View SolutionIn which cases delocalisation of charge is possible ?
View Solution
Knowledge Check
In which case racemisation takes place ?
AH3C−C2H5∣CH−CH2−BrOH−−−→SN1BCD3−C2H5∣CH−CH2BrOH−−−→SN1C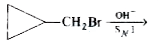
DAll of these
In which of following cases does the substance change?
View SolutionIn which case, process will be spontaneous at all temperature?
View SolutionIn which case, process will be spontaneous at all temperature?
View SolutionDependence of Spontaneity on Temperature:
For a process to be spontaneous , at constant temperature and pressure , there must be decrease in free energy of the system in the direction of the process , i.e. ΔGP.T<0.ΔGP.T=0 implies the equilibrium condition and ΔGP.T>0 corresponds to non- spontaneity.
Gibbs- Helmholtz equation relates the free energy change to the enthalpy and entropy changes of the process as : ΔGP.T=ΔH−TΔS ...(1)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS change appreciably . Thus, spontaneity of a process depends very much on temperature.
For endothermic process, both ΔH and ΔS are positive . The energy factor, the first factor of equation, opposes the spontaneity whereas entorpy factor favours it. At low temperature the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicated the nonspontaneity of the process. On raising temperature , the factor TΔS Increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous .
For an expthermic process, both ΔH and ΔS would be negative . In this case the first factor of eq.1 favours the spontaneity whereas the second factor opposes it. At high temperature , when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity fo the process . However , on decreasing temperature , the factor ,TΔS decreases rapidly and when TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus , an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
The enthalpy change for a certain rection at 300 K is −15.0 K cal mol−1 . The entropy change under these conditions is −7.2 cal K−1mol−1 . The free energy change for the reaction and its spontaneous/ non-spontaneous character will be
View SolutionWhich is/are true in case of BF3 ?
View SolutionDependence of Spontaneity on Temperature:
For a process to be spontaneous , at constant temperature and pressure , there must be decrease in free energy of the system in the direction of the process , i.e. ΔGP.T<0.ΔGP.T=0 implies the equilibrium condition and ΔGP.T>0 corresponds to non- spontaneity.
Gibbs- Helmholtz equation relates the free energy change to the enthalpy and entropy changes of the process as : ΔGP.T=ΔH−TΔS ...(1)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS change appreciably . Thus, spontaneity of a process depends very much on temperature.
For endothermic process, both ΔH and ΔS are positive . The energy factor, the first factor of equation, opposes the spontaneity whereas entorpy factor favours it. At low temperature the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicated the nonspontaneity of the process. On raising temperature , the factor TΔS Increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous .
For an expthermic process, both ΔH and ΔS would be negative . In this case the first factor of eq.1 favours the spontaneity whereas the second factor opposes it. At high temperature , when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity fo the process . However , on decreasing temperature , the factor ,TΔS decreases rapidly and when TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus , an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
A reaction has a value of ΔH=−40Kcal at 400 k cal mol−1. The reaction is spontaneous, below this temperature , it is not . The values fo ΔG and ΔS at 400 k are respectively
View SolutionDependence of Spontaneity on Temperature:
For a process to be spontaneous , at constant temperature and pressure , there must be decrease in free energy of the system in the direction of the process , i.e. ΔGP.T<0.ΔGP.T=0 implies the equilibrium condition and ΔGP.T>0 corresponds to non- spontaneity.
Gibbs- Helmholtz equation relates the free energy change to the enthalpy and entropy changes of the process as : ΔGP.T=ΔH−TΔS ...(1)
The magnitude of ΔH does not change much with the change in temperature but the entropy factor TΔS change appreciably . Thus, spontaneity of a process depends very much on temperature.
For endothermic process, both ΔH and ΔS are positive . The energy factor, the first factor of equation, opposes the spontaneity whereas entorpy factor favours it. At low temperature the favourable factor TΔS will be small and may be less than ΔH,ΔG will have positive value indicated the nonspontaneity of the process. On raising temperature , the factor TΔS Increases appreciably and when it exceeds ΔH,ΔG would become negative and the process would be spontaneous .
For an expthermic process, both ΔH and ΔS would be negative . In this case the first factor of eq.1 favours the spontaneity whereas the second factor opposes it. At high temperature , when TΔS>ΔH,ΔG will have positive value, showing thereby the non-spontaneity fo the process . However , on decreasing temperature , the factor ,TΔS decreases rapidly and when TΔS<ΔH,ΔG becomes negative and the process occurs spontaneously. Thus , an exothermic process may be spontaneous at low temperature and non-spontaneous at high temperature.
For the reaction at 298K,2A+B→C
ΔH=100kcal and ΔS=0.050kcalK−1. If ΔH and ΔS are assumed to be constant over the temperature range, above what temperature will the reaction become spontaneous?
View Solution