The standard heat of combustion of is at . If reacts with at , which of the following release of heat?
The reaction of
The formation fo
The reaction of
The formation of
To solve the problem, we need to determine how much aluminum (Al) is required to release 250 kJ of heat based on the standard heat of combustion of aluminum, which is given as -837.8 kJ/mol at 25°C.
1. Understand the Heat of Combustion:
The heat of combustion of aluminum is -837.8 kJ/mol. This means that when 1 mole of aluminum combusts, it releases 837.8 kJ of heat.
2. Set Up the Proportion:
We need to find out how many moles of aluminum are required to release 250 kJ of heat. We can set up a proportion based on the heat released per mole:
Heat released by 1 mole of Al=837.8 kJ
Heat released by x moles of Al=250 kJ
3. Calculate the Moles of Aluminum:
Using the proportion, we can calculate the moles of aluminum (x) required to release 250 kJ:
x=250 kJ837.8 kJ/mol≈0.298 mol
Rounding this, we find:
x≈0.3 mol
4. Determine the Amount of Aluminum Oxide Formed:
According to the stoichiometry of the combustion reaction, 1 mole of aluminum produces 0.5 moles of aluminum oxide (Al₂O₃). Therefore, if we have 0.3 moles of aluminum, the amount of aluminum oxide produced will be:
Moles of Al₂O₃=0.3 mol Al×1 mol Al₂O₃2 mol Al=0.15 mol Al₂O₃
5. Conclusion:
The correct answer for the amount of aluminum oxide formed when 250 kJ of heat is released is 0.15 moles of Al₂O₃.
Final Answer:
The correct answer is D (0.15 moles of Al₂O₃).
The heat of combustion of aluminum is -837.8 kJ/mol. This means that when 1 mole of aluminum combusts, it releases 837.8 kJ of heat.
We need to find out how many moles of aluminum are required to release 250 kJ of heat. We can set up a proportion based on the heat released per mole:
Heat released by 1 mole of Al=837.8 kJ
Heat released by x moles of Al=250 kJ
Using the proportion, we can calculate the moles of aluminum (x) required to release 250 kJ:
x=250 kJ837.8 kJ/mol≈0.298 mol
Rounding this, we find:
x≈0.3 mol
According to the stoichiometry of the combustion reaction, 1 mole of aluminum produces 0.5 moles of aluminum oxide (Al₂O₃). Therefore, if we have 0.3 moles of aluminum, the amount of aluminum oxide produced will be:
Moles of Al₂O₃=0.3 mol Al×1 mol Al₂O₃2 mol Al=0.15 mol Al₂O₃
The correct answer for the amount of aluminum oxide formed when 250 kJ of heat is released is 0.15 moles of Al₂O₃.
The correct answer is D (0.15 moles of Al₂O₃).
Topper's Solved these Questions
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercises (Assertion-Reasoning)
23 Videos
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercises (Interger)
10 Videos
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Multiple correct Answer Type
2 Videos
- STOICHIOMETRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STOICHIOMETRYEXERCISE - Archives Subjective
33 Videos
Similar Questions
Knowledge Check
The combustion of benzene(/) gives CO2(g)andH2O(l) Given that heat of combustion of benzene at constant volume is −3263.9kJmol−1 at 25∘C, heat of combustion (in kJ mol−1) of benzene at constant pressure will be
(R=8.314JK−1mol−1)A4152.6B−452.46C3260D−3267.6
the standard heat of formation of Fe2O3 (s) is 824.2kJ mol-1 Calculate heat change for the reaction. 4Fe(s) + 302 (g)= 2Fe2O3(s)
View SolutionThe combustion of benzene (l) gives CO2(g) and H2O(l). Given that heat of combustion of benzene at constant volume is –3263.9kJmol–1 at 25∘C, heat of combustion (in kJmol–1) of benzene at constant pressure will be
(R = 8.314 JK–1 mol–1)
View SolutionThe standard free energy change for a reaction is −213.3KJmol−1at25∘C. If the enthalpy change of the reaction is −217.77KJmole−1 . Calculate the magnitude of entropy change for the reaction in Joule mole−1
View SolutionEthylene on combustion gives carbon dioxide and water. Its heat of combustion is 1410.0kJmol−1. If the heat of formation of CO2 and H2O are 393.3kJ and 286.2kJ, respectively. Calculate the heat of formation of ethylene.
View SolutionEthylene on combustion gives carbon dioxide and water. Its heat of combustion is 1410.0kJmol−1. If the heat of formation of CO2 and H2O are 393.3kJ and 286.2kJ, respectively. Calculate the heat of formation of ethylene.
View SolutionThe standard potential of a cell using the reaction
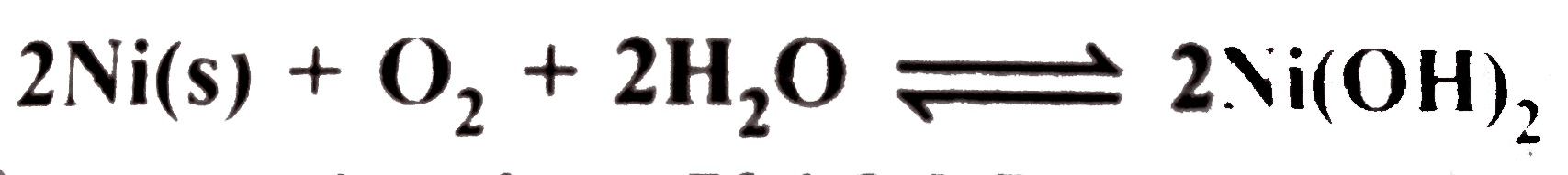 is 1.12. The heat of the reaction is −504.2kJmol−1 at 25∘C. Calculate the entropy change.
is 1.12. The heat of the reaction is −504.2kJmol−1 at 25∘C. Calculate the entropy change.
View SolutionThe heat of combustion of sucrose C12H22O11(s) at constant volume is -1348.9 kcal mol−1 at 25∘C, then the heat of reaction at constant pressure, when steam is producced, is
View Solution
