A heated irron block at 127∘C loses 300J of heat to the surroundings which are at a temperature of 27∘C. This process is 0.05xJK−1. Find the value of x.
To solve the problem, we need to calculate the total entropy change of the system and the surroundings when the heated iron block loses heat. Here’s a step-by-step breakdown of the solution:
Step 1: Identify the Given Data
- Temperature of the iron block (T_system) = 127°C = 127 + 273 = 400 K
- Temperature of the surroundings (T_surroundings) = 27°C = 27 + 273 = 300 K
- Heat lost by the iron block (Q_system) = 300 J
- Total entropy change is given as 0.05x J/K.
Step 2: Calculate the Entropy Change of the System
The entropy change of the system (ΔS_system) when it loses heat is calculated using the formula:
ΔSsystem=−QsystemTsystem
Substituting the values:
ΔSsystem=−300J400K=−0.75J/K
Step 3: Calculate the Entropy Change of the Surroundings
The entropy change of the surroundings (ΔS_surroundings) when it gains heat is calculated using the formula:
ΔSsurroundings=QsystemTsurroundings
Substituting the values:
ΔSsurroundings=300J300K=1.0J/K
Step 4: Calculate the Total Entropy Change
The total entropy change (ΔS_total) is the sum of the entropy changes of the system and the surroundings:
ΔStotal=ΔSsystem+ΔSsurroundings
Substituting the values:
ΔStotal=−0.75J/K+1.0J/K=0.25J/K
Step 5: Relate Total Entropy Change to Given Expression
According to the problem, the total entropy change is also expressed as:
ΔStotal=0.05xJ/K
Setting the two expressions for total entropy equal to each other:
0.05x=0.25
Step 6: Solve for x
To find the value of x, we rearrange the equation:
x=0.250.05=5
Final Answer
The value of x is 5.
---
- Temperature of the iron block (T_system) = 127°C = 127 + 273 = 400 K
- Temperature of the surroundings (T_surroundings) = 27°C = 27 + 273 = 300 K
- Heat lost by the iron block (Q_system) = 300 J
- Total entropy change is given as 0.05x J/K.
The entropy change of the system (ΔS_system) when it loses heat is calculated using the formula:
ΔSsystem=−QsystemTsystem
Substituting the values:
ΔSsystem=−300J400K=−0.75J/K
The entropy change of the surroundings (ΔS_surroundings) when it gains heat is calculated using the formula:
ΔSsurroundings=QsystemTsurroundings
Substituting the values:
ΔSsurroundings=300J300K=1.0J/K
The total entropy change (ΔS_total) is the sum of the entropy changes of the system and the surroundings:
ΔStotal=ΔSsystem+ΔSsurroundings
Substituting the values:
ΔStotal=−0.75J/K+1.0J/K=0.25J/K
According to the problem, the total entropy change is also expressed as:
ΔStotal=0.05xJ/K
Setting the two expressions for total entropy equal to each other:
0.05x=0.25
To find the value of x, we rearrange the equation:
x=0.250.05=5
The value of x is 5.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercises (Fill In The Blanks)
52 Videos
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercises (True/False)
32 Videos
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercises (Assertion-Reasoning)
23 Videos
- STOICHIOMETRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STOICHIOMETRYEXERCISE - Archives Subjective
33 Videos
Similar Questions
A heated copper block at 130∘C loses 340 J of heat to the surroundings, which are at room temperature of 32∘C. Calculate total entropy change in the universe due to this process.
View SolutionCorresponding to the process shown in figure, the heat given to the gas in the process ABCA is (0.2x)J. Find value of x.
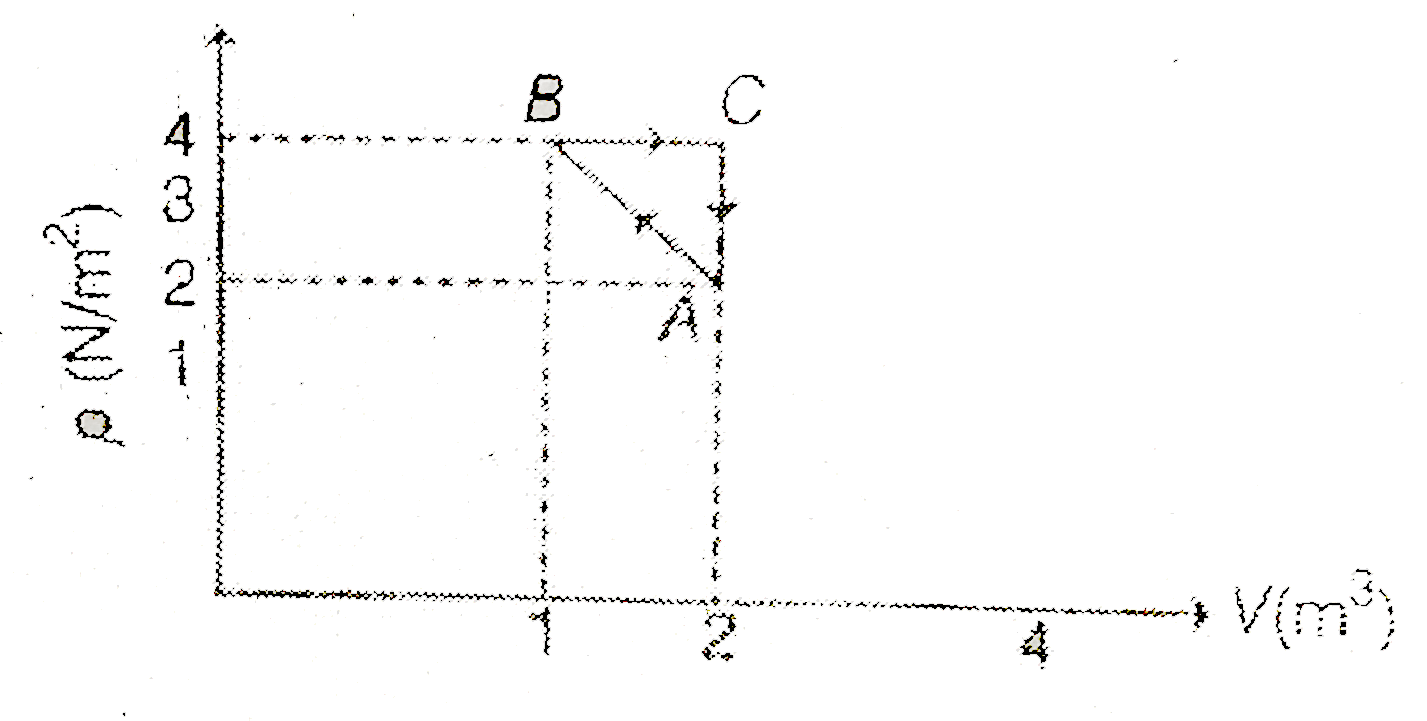
View Solution
Knowledge Check
A Carnot engine absorbs 750 J of heat energy from a reservoir at 137∘C and rejects 500 J of heat during each cycle then the temperature of sink is
A0.25∘CB0.34∘CC0.44∘CD0.54∘C
50 g of metal piece at 27∘C requires 2400 J of heat energy so as to attain a temperature of 327∘C. Calculate the specific heat capacity of the metal.
View SolutionA heat engine rejects 600 cal to the sink at 27∘C . Amount of work done by the engine will be
(Temperature of source is 227∘C & J = 4.2 J/cal )
View SolutionA certain process releases 64.0 kJ of heat, which is transferred to the surroundings at a constant pressure and a constant temperature of 300 K. For this process ΔSsurr is:
View SolutionA metal piece of mass 50 g at 27∘C requires 2400 J of heat energy in order to raise its temperature to 327∘C. Calculate the specific heat capacity of the metal.
View SolutionA scientist says that the efficiency of his heat engine which operates at source temperature 127∘C and sink temperature 27∘Cis26%, then
View SolutionA scientist says that the efficiency of his heat engine which operates at source temperature 127∘C and sink temperature 27∘Cis26%, then
View SolutionA scientist says that the efficiency of his heat engine which operates at source temperature 127∘C and sink temperature 27∘C is 26%, then
View Solution
