Cv values of He is always 3R2 but Cv values of H2 is 3R2
at low temperature and 5R2 at higher temperature explain .
To explain the difference in the molar heat capacity at constant volume (C_v) values of helium (He) and hydrogen (H₂) at various temperatures, we need to consider the molecular structure and degrees of freedom of these gases.
1. Understanding C_v:
- C_v is the molar heat capacity at constant volume, which indicates how much heat is required to raise the temperature of one mole of a substance by one degree Celsius at constant volume.
2. C_v of Helium (He):
- Helium is a monoatomic gas. Monoatomic gases have only translational degrees of freedom.
- The formula for C_v for a monoatomic ideal gas is given by:
Cv=32R
- Therefore, for helium, C_v is always:
Cv=3R2
3. C_v of Hydrogen (H₂) at Low Temperature:
- Hydrogen is a diatomic molecule. At low temperatures, the rotational and vibrational contributions to the heat capacity are negligible (considered as zero).
- For diatomic gases at low temperatures, the only active degrees of freedom are translational.
- Thus, the C_v for hydrogen at low temperature is:
Cv=32R
4. C_v of Hydrogen (H₂) at Moderate Temperature:
- As the temperature increases to moderate levels, the rotational degrees of freedom become active, while vibrational contributions remain negligible.
- For diatomic gases, the degrees of freedom at moderate temperatures are:
- Translational: 3
- Rotational: 2
- Therefore, the total degrees of freedom become 5, leading to:
Cv=52R
5. C_v of Hydrogen (H₂) at High Temperature:
- At high temperatures, both rotational and vibrational degrees of freedom become active.
- For diatomic gases at high temperatures, the degrees of freedom are:
- Translational: 3
- Rotational: 2
- Vibrational: 2
- Thus, the total degrees of freedom become 7, resulting in:
Cv=72R
Summary of Results:
- For helium (He):
Cv=3R2(always)
- For hydrogen (H₂):
- At low temperature:
Cv=3R2
- At moderate temperature:
Cv=5R2
- At high temperature:
Cv=7R2
- C_v is the molar heat capacity at constant volume, which indicates how much heat is required to raise the temperature of one mole of a substance by one degree Celsius at constant volume.
- Helium is a monoatomic gas. Monoatomic gases have only translational degrees of freedom.
- The formula for C_v for a monoatomic ideal gas is given by:
Cv=32R
- Therefore, for helium, C_v is always:
Cv=3R2
- Hydrogen is a diatomic molecule. At low temperatures, the rotational and vibrational contributions to the heat capacity are negligible (considered as zero).
- For diatomic gases at low temperatures, the only active degrees of freedom are translational.
- Thus, the C_v for hydrogen at low temperature is:
Cv=32R
- As the temperature increases to moderate levels, the rotational degrees of freedom become active, while vibrational contributions remain negligible.
- For diatomic gases, the degrees of freedom at moderate temperatures are:
- Translational: 3
- Rotational: 2
- Therefore, the total degrees of freedom become 5, leading to:
Cv=52R
- At high temperatures, both rotational and vibrational degrees of freedom become active.
- For diatomic gases at high temperatures, the degrees of freedom are:
- Translational: 3
- Rotational: 2
- Vibrational: 2
- Thus, the total degrees of freedom become 7, resulting in:
Cv=72R
- For helium (He):
Cv=3R2(always)
- For hydrogen (H₂):
- At low temperature:
Cv=3R2
- At moderate temperature:
Cv=5R2
- At high temperature:
Cv=7R2
Topper's Solved these Questions
Similar Questions
The molar heat capacity , Cv of helium gas is 3/2R and is independent of temperature. For hydrogen gas, Cv approaches 3/2R at very low temperature, equal 5/2R at moderate temperature and is higher than 5/2R at high temperatures. Give a reason for the temperature dependence of Cv in case of hydrogen, in not more than two or three sentences.
View SolutionThe value of CV for monatomic gas is 32R, then CP will be
View SolutionTwo resistance R1 and R2 are made of different material. The temperature coefficient of the material of R1 is α and of the material of R2 is −β. Then resistance of the series combination of R1 and R2 will not change with temperature, if R1/R2 will not change with temperature if R1/R2 equals
View SolutionTwo resistance R1 and R2 are made of different material. The temperature coefficient of the material of R1 is α and of the material of R2 is −β. Then resistance of the series combination of R1 and R2 will not change with temperature, if R1/R2 will not change with temperature if R1/R2 equals
View SolutionValue of Cp for monatomic gas is 52R. Find CV.
View SolutionA sample consisting of 1 mole of a mono-atomic perfect gas (Cv=32R) is taken through the cycle as shown.

Temperature at points (1), (2) and (3), respectively is:
View SolutionA sample consisting of 1mol of a mono-atomic perfect gas (CV=32R) is taken through the cycle as shown.
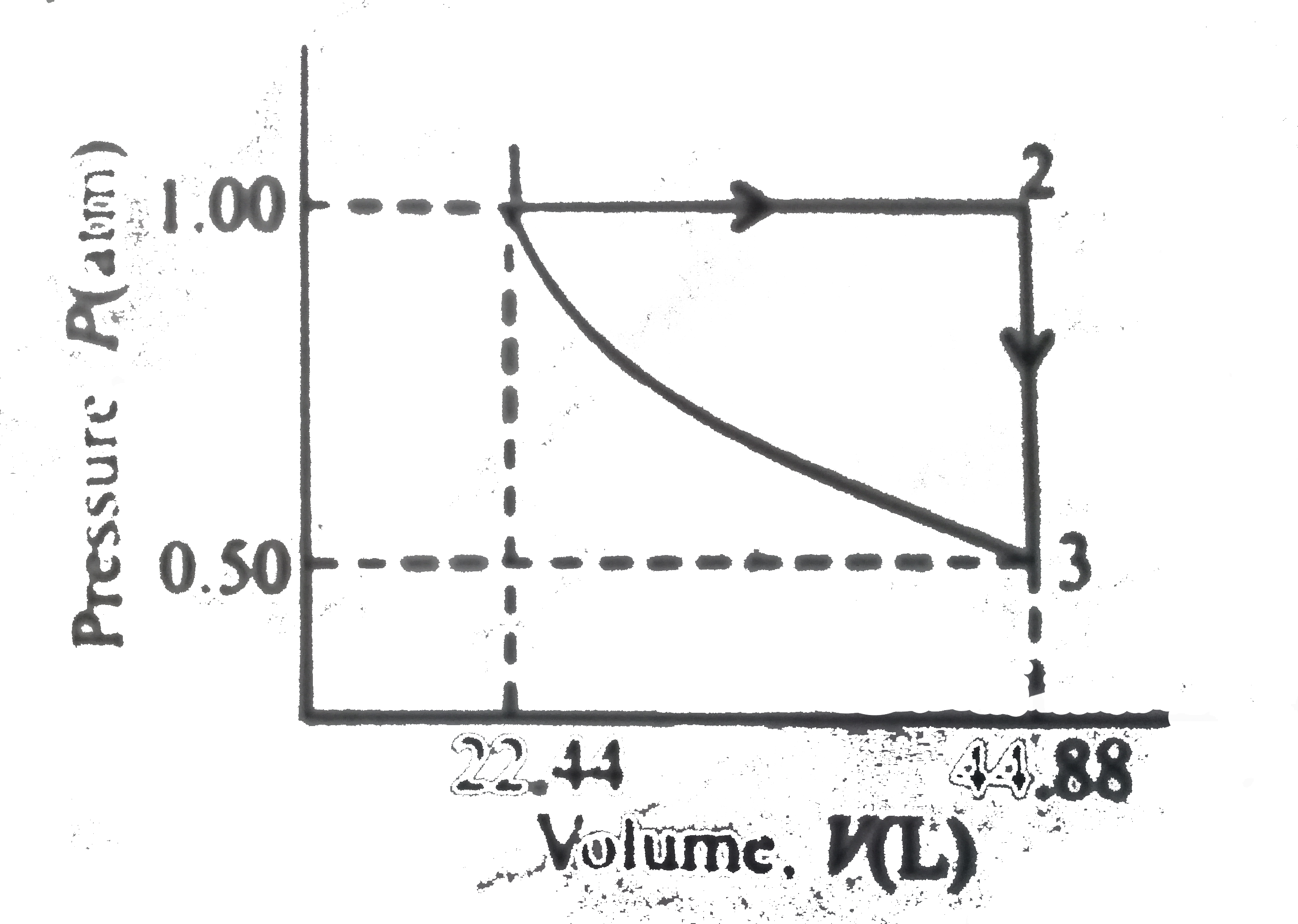
Temperature at points (1),(2) and (3) respectively is
View SolutionTwo moles the an ideal gas with Cv=32R are mixed with 3 of anthoer ideal gas with Cv=52R . The value of the Cp for the mixture is :
View SolutionTwo moles the an ideal gas with Cv=32R are mixed with 3 of anthoer ideal gas with Cv=52R . The value of the Cp for the mixture is :
View SolutionThe value of b−cr1+c−ar2+a−br3 is equal to
View Solution