The vapour density of N2O4 at a certain temperature is 30. Calculate the percentage dissociation of N2O4 this temperature.
To solve the problem of calculating the percentage dissociation of N2O4 given its vapor density, we can follow these steps:
Step 1: Calculate the Molar Mass from Vapor Density
The vapor density (VD) is given as 30. The molar mass (M) can be calculated using the formula:
M=2×Vapor Density
Substituting the value:
M=2×30=60g/mol
Step 2: Write the Dissociation Reaction
The dissociation of N2O4 can be represented as:
N2O4⇌2NO2
Step 3: Set Up the Initial and Equilibrium Concentrations
Assume we start with 1 mole of N2O4 and let α be the degree of dissociation. At equilibrium:
- Moles of N2O4 = 1−α
- Moles of NO2 = 2α
Step 4: Calculate Total Moles at Equilibrium
The total moles at equilibrium will be:
Total moles=(1−α)+2α=1+α
Step 5: Calculate the Average Molar Mass at Equilibrium
The average molar mass at equilibrium can be calculated using the mole fractions of each species:
Average Molar Mass=(MN2O4⋅moles of N2O4)+(MNO2⋅moles of NO2)Total moles
Where:
- MN2O4=92g/mol
- MNO2=46g/mol
Substituting the values:
Average Molar Mass=(92⋅(1−α))+(46⋅2α)1+α
Step 6: Set the Average Molar Mass Equal to the Calculated Molar Mass
We know the average molar mass from the vapor density is 60 g/mol. Therefore, we set up the equation:
(92⋅(1−α))+(46⋅2α)1+α=60
Step 7: Solve for α
Multiply both sides by (1+α):
92(1−α)+92α=60(1+α)
Expanding and rearranging gives:
92−92α+92α=60+60α
92=60+60α
32=60α
α=3260=0.5333
Step 8: Calculate the Percentage Dissociation
The percentage dissociation is given by:
Percentage Dissociation=α×100=0.5333×100=53.33%
Final Answer
The percentage dissociation of N2O4 at this temperature is 53.33%.
---
The vapor density (VD) is given as 30. The molar mass (M) can be calculated using the formula:
M=2×Vapor Density
Substituting the value:
M=2×30=60g/mol
The dissociation of N2O4 can be represented as:
N2O4⇌2NO2
Assume we start with 1 mole of N2O4 and let α be the degree of dissociation. At equilibrium:
- Moles of N2O4 = 1−α
- Moles of NO2 = 2α
The total moles at equilibrium will be:
Total moles=(1−α)+2α=1+α
The average molar mass at equilibrium can be calculated using the mole fractions of each species:
Average Molar Mass=(MN2O4⋅moles of N2O4)+(MNO2⋅moles of NO2)Total moles
Where:
- MN2O4=92g/mol
- MNO2=46g/mol
Average Molar Mass=(92⋅(1−α))+(46⋅2α)1+α
We know the average molar mass from the vapor density is 60 g/mol. Therefore, we set up the equation:
(92⋅(1−α))+(46⋅2α)1+α=60
Multiply both sides by (1+α):
92(1−α)+92α=60(1+α)
Expanding and rearranging gives:
92−92α+92α=60+60α
92=60+60α
32=60α
α=3260=0.5333
The percentage dissociation is given by:
Percentage Dissociation=α×100=0.5333×100=53.33%
The percentage dissociation of N2O4 at this temperature is 53.33%.
Topper's Solved these Questions
- CHEMICAL EQUILIBRIUMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Concept Applicationexercise 7.1
53 Videos
- CHEMICAL EQUILIBRIUMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Ex 7.2
40 Videos
- CHEMICAL BONDING AND MOLECULAR STRUCTUREBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTUREEXERCISE - Archives Subjective
15 Videos
- CLASSIFICATION AND NOMENCLATURE OF ORGANIC COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CLASSIFICATION AND NOMENCLATURE OF ORGANIC COMPOUNDSEXERCISE - Analytical and Descriptive Type
3 Videos
Similar Questions
Knowledge Check
The average kinetic energy of O2 at a particular temperatures is 0.768 eV. The average kinetic energy of N2 molecules in eV at the same temperature is
A0.0015B0.0030C0.048D0.768
The equilibrium constant (KP) of the reactions N2O4⇔2NO2 was found to be 636 mm at 49.7∘C . Calculate the percentage dissociation of N2O4 when the pressure of the gas mixture is 182 mm.
View SolutionDuring thermal dissociation, the observed vapour density of N2O4(g) is 26.0. The extent of dissociation of N2O4 is:
View SolutionThe equilibrium constant Kp for the reaction
N2O4(g)⇔2NO2(g)
at 497∘C is found to be 636mmHg. If the pressure of the gas mixture is 182mm, calculate the presentage dissociation of N2O4. At what pressure will it be dissociated?
View Solution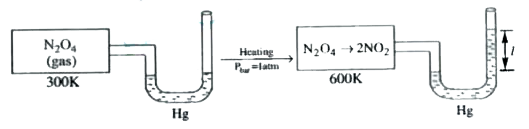
If the value of l in the above diagram is 114 cm. What is the percentage dissociation of N2O4 due to heating.
View SolutionThe ratio of the rate of diffusion of a sample of N2O4 partially dissociated in to NO2 to pure hydrogen was found to be 1:5 . Calculate the degree of dissociation of N2O4.
View SolutionFor the dissociation reaction
N2O4(g)⇔2NO2(g),
the equilibrium constant KP is 0.120 atm at 298K and total pressure of system is 2 atm. Calculate the degree of dissociation of N2O4.
View SolutionN2O4 is a mixed anhydride because it
View Solution
