Calculate the entropy of ΘOH ion at 298K. Given:
a. H2O⇔H⊕+ΘOH(ΔH=13.4kcal)
b. Keq for the reaction =10−14.
c. SΘ(H⊕)=0.0
d. SΘ(H2O)=16.7cal/molk.
To calculate the entropy of the OH− ion at 298K, we will follow these steps:
Step 1: Write the reaction and identify the given data
The reaction is:
\( H_2O \rightleftharpoons H^+ + OH^- \)
Given data:
- \(\Delta H = 13.4 \, \text{kcal}\)
- \(K_{eq} = 10^{-14}\)
- \(S^\Theta(H^+) = 0.0 \, \text{cal/mol K}\)
- \(S^\Theta(H_2O) = 16.7 \, \text{cal/mol K}\)
Step 2: Calculate \(\Delta G^\Theta\)
Using the equation:
\(
\Delta G^\Theta = -2.303 \times R \times T \times \log K_{eq}
\)
Where:
- \(R = 1.987 \, \text{cal/mol K}\)
- \(T = 298 \, \text{K}\)
- \(K_{eq} = 10^{-14}\)
Substituting the values:
\(
\Delta G^\Theta = -2.303 \times 1.987 \times 298 \times \log(10^{-14})
\)
Calculating \(\log(10^{-14}) = -14\):
\(
\Delta G^\Theta = -2.303 \times 1.987 \times 298 \times (-14)
\)
Calculating this gives:
\(
\Delta G^\Theta \approx 19.1 \, \text{kcal/mol}
\)
Step 3: Use the Gibbs free energy relation to find \(\Delta S^\Theta\)
Using the relation:
\(
\Delta G^\Theta = \Delta H^\Theta - T \Delta S^\Theta
\)
Rearranging gives:
\(
\Delta S^\Theta = \frac{\Delta H^\Theta - \Delta G^\Theta}{T}
\)
Substituting the values:
\(
\Delta S^\Theta = \frac{13.4 \, \text{kcal/mol} - 19.1 \, \text{kcal/mol}}{298 \, \text{K}}
\)
Calculating this:
\(
\Delta S^\Theta = \frac{-5.7 \, \text{kcal/mol}}{298 \, \text{K}} \approx -0.0192 \, \text{kcal/mol K} \approx -19.2 \, \text{cal/mol K}
\)
Step 4: Calculate the entropy of OH−
Using the equation for entropy change:
\(
\Delta S^\Theta = S^\Theta(H^+) + S^\Theta(OH^-) - S^\Theta(H_2O)
\)
Substituting the known values:
\(
-19.2 \, \text{cal/mol K} = 0 + S^\Theta(OH^-) - 16.7 \, \text{cal/mol K}
\)
Rearranging gives:
\(
S^\Theta(OH^-) = -19.2 + 16.7
\)
Calculating this:
\(
S^\Theta(OH^-) = -2.5 \, \text{cal/mol K}
\)
Final Answer
The entropy of the OH− ion at 298K is:
\(
S^\Theta(OH^-) = -2.5 \, \text{cal/mol K}
\)
The reaction is:
\( H_2O \rightleftharpoons H^+ + OH^- \)
Given data:
- \(\Delta H = 13.4 \, \text{kcal}\)
- \(K_{eq} = 10^{-14}\)
- \(S^\Theta(H^+) = 0.0 \, \text{cal/mol K}\)
- \(S^\Theta(H_2O) = 16.7 \, \text{cal/mol K}\)
Using the equation:
\(
\Delta G^\Theta = -2.303 \times R \times T \times \log K_{eq}
\)
Where:
- \(R = 1.987 \, \text{cal/mol K}\)
- \(T = 298 \, \text{K}\)
- \(K_{eq} = 10^{-14}\)
\(
\Delta G^\Theta = -2.303 \times 1.987 \times 298 \times \log(10^{-14})
\)
Calculating \(\log(10^{-14}) = -14\):
\(
\Delta G^\Theta = -2.303 \times 1.987 \times 298 \times (-14)
\)
Calculating this gives:
\(
\Delta G^\Theta \approx 19.1 \, \text{kcal/mol}
\)
Using the relation:
\(
\Delta G^\Theta = \Delta H^\Theta - T \Delta S^\Theta
\)
Rearranging gives:
\(
\Delta S^\Theta = \frac{\Delta H^\Theta - \Delta G^\Theta}{T}
\)
Substituting the values:
\(
\Delta S^\Theta = \frac{13.4 \, \text{kcal/mol} - 19.1 \, \text{kcal/mol}}{298 \, \text{K}}
\)
Calculating this:
\(
\Delta S^\Theta = \frac{-5.7 \, \text{kcal/mol}}{298 \, \text{K}} \approx -0.0192 \, \text{kcal/mol K} \approx -19.2 \, \text{cal/mol K}
\)
Using the equation for entropy change:
\(
\Delta S^\Theta = S^\Theta(H^+) + S^\Theta(OH^-) - S^\Theta(H_2O)
\)
Substituting the known values:
\(
-19.2 \, \text{cal/mol K} = 0 + S^\Theta(OH^-) - 16.7 \, \text{cal/mol K}
\)
Rearranging gives:
\(
S^\Theta(OH^-) = -19.2 + 16.7
\)
Calculating this:
\(
S^\Theta(OH^-) = -2.5 \, \text{cal/mol K}
\)
The entropy of the OH− ion at 298K is:
\(
S^\Theta(OH^-) = -2.5 \, \text{cal/mol K}
\)
Topper's Solved these Questions
- IONIC EQUILIBRIUMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - IONIC EQUILIBRIUMEXERCISE - Ex 8.1
18 Videos
- IONIC EQUILIBRIUMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - IONIC EQUILIBRIUMEXERCISE - Ex 8.2
27 Videos
- HYDROGEN, WATER AND HYDROGEN PEROXIDEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - HYDROGEN, WATER AND HYDROGEN PEROXIDEEXERCISE - Subjective Archive (Subjective)
3 Videos
- ISOMERISMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ISOMERISMEXERCISE - Assertion-Reasoning Type
1 Videos
Similar Questions
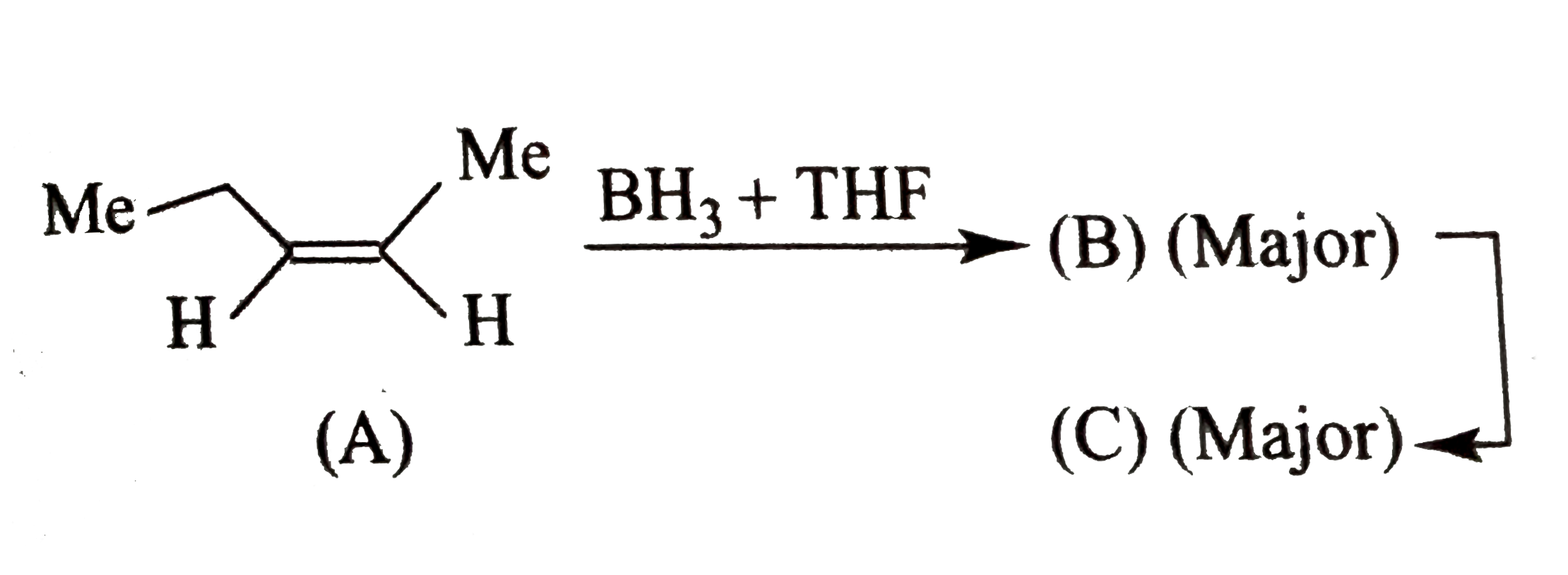 H2O2+ΘOH
H2O2+ΘOH
B and C are:
View Solution2H2O⇔H3O⊕+ΘOH,Kw=10−14 at 25∘C, hence Ka is
View SolutionCalculated the equilibrium constant for the following reaction at 298K:
2H2O(l)→2H2(g)+O2(g)
ΔfGΘ(H2O)=−237.2kJmol−1,R=8.314Jmol−1K−1
View SolutionCalculate Ksp for AgCI. Given:
ΔfHΘAg⊕=25.3kcalmol−1
ΔfHΘC1Θ=−40.0kcalmol−1
ΔfHΘAgC1=−30.36kcalmol−1
SΘAg⊕,SΘC1Θ, and SΘAgC1are 17.7,13.2 and 23.0calmol−1
View SolutionThe enthalpy change (ΔH) of the reaction at 298 K
C2H5OH(l)+3O2(g)→2CO2(g)+3H2O(l)
is found to be -326.7 kcal. Calculate ΔE for the given reaction.
View SolutionCalculate [H⊕] and [ΘOH] in 10−3M solution of monobasic acid which is 4.0% ionised. What is the pH,Ka and pKa of the acid.
View SolutionThe standard potential of the reaction
H2O+e−→(12)H2+OH− at 298 K by using kw(H2O)=10−14, is:
View SolutionCalculate heat of dissociation for acetic acid from the following data:
CH3COOH+NaOH→CH3COONa+H2OΔH=−13.2kcal
H⊕+ΘOH→H2O,ΔH=−13.7kcal
Also calculate heat of dissociation for NH4OH if
HCI+NH4OH→NH4CI+H2O,ΔH=−12.27kcal
View SolutionCalculate K for the reaction, A−+H+3O⇔HA+H2O
if Ka value for the acid HA is 1.0×10−6.
View SolutionCalculate K for the reaction, A−+H+3O⇔HA+H2O
if Ka value for the acid HA is 1.0×10−6.
View Solution
